 Сего дня мы продолжим рассмотрение техник научного менеджмента в применении к управлению проектами. В частности, данная заметка будет продолжением моего описания алгоритма построения графика распределения вероятности для объектов воздействия рисков. Для этого мы рассмотрим, что такое процесс бинаризации, как его применить для более адекватной оценки прогнозных сводных значений, а также посмотрим на реализацию данного алгоритма на прекраснейшем языке программирования Haskell.
Сего дня мы продолжим рассмотрение техник научного менеджмента в применении к управлению проектами. В частности, данная заметка будет продолжением моего описания алгоритма построения графика распределения вероятности для объектов воздействия рисков. Для этого мы рассмотрим, что такое процесс бинаризации, как его применить для более адекватной оценки прогнозных сводных значений, а также посмотрим на реализацию данного алгоритма на прекраснейшем языке программирования Haskell.
Хотелось бы сразу предупредить, что в статье есть немного «матана», так что для её чтения желательно иметь базовые представления о теории вероятности. В частности, необходимо понимание формул для умножения и сложения вероятностей для независимых событий. Более серьёзные темы из теории вероятностей здесь не рассматриваются.
Постановка задачи
Не секрет, что руководители часто хотят получить прогнозное сводное значение для оценки каких-либо параметров, точные значения которых неизвестны, они могут быть получены только в будущем (если вообще могут быть получены), а оценка требуется уже сейчас. Это могут быть:
- Сдвиг сроков сдачи проекта из-за воздействия рисков или неопределённостей.
- Увеличение бюджета проекта также из-за воздействия рисков и неопределённостей.
- Суммарный прогноз по выручке, полученной с пресейлов при условии преобразования некоторых из них в проекты.
- ...
- Вообще в любой задаче получения суммарного прогнозного значения по имеющимся прогнозным значениям с приписанным им оценкам вероятности.
Например, уже сейчас во многих организациях ведётся бюджетирование проектной деятельности на будущий, 2013 год. Как происходит этот процесс? Обычно главное ЛПР (лицо, принимающее решение) собирает ЛПР рангом пониже и задаёт вопрос: «Какие проекты и за сколько денег у вас будут сделаны в будущем году?». ЛПР рангом пониже начинают суетиться и бегать, вызывают своих менеджеров по продажам и задают им тот же вопрос. А менеджеры по продажам отвечают: «Ну-у-у, вот проект X за X' миллионов мы получим с вероятностью 50 %, а проект Y за Y' миллионов мы получим уж точно, но на всякие непредвиденные обстоятельства скинем 10 %, так что получится здравая оценка в 90 %». И такие данные собираются по всему набору будущих проектов.
Если бы после этого оценка будущих поступлений производилась бы адекватным образом, то надобности в данной статье бы не было в принципе. Однако далее, когда все подобные данные собраны, то есть получено множество оценок вида (xi, pi), где pi — вероятность получения проекта xi, начинается самое интересное. Главное ЛПР, не долго думая, берёт формулу из учебников по стратегическому менеджменту и вычисляет:
Формула (1): 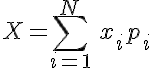
Даже не смотря на то, что в некоторых учебниках написано, что применять эту формулу необходимо с осмотрительностью и только в случаях, когда число проектов N достаточно велико, многие применяют её и для десятка проектов. В итоге выходит совершенно нелогичное и ничем не обоснованное значение, которое вписывается в планы продаж. Ну а по итогам года наступает резонное разочарование — «средней температуры по больнице» добиться практически невозможно. Даже с теми или иными требованиями к точности.
Пояснить вышесказанное можно при помощи рассмотрения одного граничного случая. Пусть от продающих подразделений пришли данные: «В 2013 году мы продадим проект X стоимостью 10 млн. руб. с вероятностью 50 %, а проект Y стоимостью 100 млн. руб. с вероятностью 50 %. Указанная выше формула даст оценку: 55 млн. руб. Главное ЛПР посмотрит, хмыкнет и запишет в план: «Продать услуг на 50 млн. руб.». Прекрасно. Но если подумать чуть глубже, то станет ясно, что такого числа на горизонте вообще нет — проектов будет продано либо на 0, либо на 10, либо на 100, либо на 110 млн. руб, причём с равными вероятностями в 25 %. Никаких 50 или 55 млн. руб. тут нет и никогда не было.
Ну и то же самое можно сказать про управление рисками. Если руководитель проектов оценивает риски подобным образом, то его ждёт очень серьёзное разочарование по результатам выполнения работ по проекту. И отсутствие премии по итогам — это самое малое зло, что может его ждать.
Процесс бинаризации
В чём суть проблемы? Люди, умудрённые в математике, уже увидели, что для оценки прогнозного суммарного значения используется банальная формула для вычисления математического ожидания (для дискретных величин). При этом, как я полагаю, полагаются на закон больших чисел, когда считается, что для достаточно большой выборки эмпирическое среднее будет стремиться к теоретическому среднему. Именно поэтому приведённый выше пример был абсурдным — ни о каких больших числах речи там не идёт, два проекта — это нерепрезентативная выборка.
Но тут возникает вопрос. А сколько проектов репрезентативно? Десять проектов — достаточно для применения подобного подхода? А сто? В моём личном опыте этот подход применялся для расчёта по 10 — 15 будущим проектам. ЛПР получали среднюю оценку и удовлетворялись ею полностью. А через полгода начинали рвать волосы на всех местах — планы заваливались.
Как быть? Как получить более адекватную оценку, чтобы иметь возможность принимать решение не в условиях полной неопределённости, а хоть как-то основываясь на более строгом математическом аппарате. Решение есть, и оно довольно простое. Бинаризация, как я называю этот процесс, позволяет более адекватно оценить прогнозные значения сводных параметров.
Суть бинаризации заключается в рассмотрении всего множества вероятных исходов нескольких независимых событий. Независимость — это очень важно, поскольку в данном случае мы можем обойтись умножением и сложением вероятностей, не привлекая такие формализмы, как сети Байеса. Впрочем, есть мнение, что чисто независимых событий найти не удастся, процесс бинаризации можно применять и для «примерно независимых» событий. Под этим термином я понимаю ситуацию, когда мы не можем оценить независимость событий, а потому считаем их независимыми. Это, конечно, очень сильное требование, но оно требуется для описываемого подхода.
Пусть у нас есть N пар вида (xi, pi), где xi — некоторое вероятное значение, а pi — вероятность его проявления. Тогда, естественно, (1 — pi) будет вероятностью непроявления соответствующего значения. Под значением мы здесь понимаем некоторую числовую характеристику — стоимость потенциального контракта, количество добавляемых к сроку сдачи проекта дней и т. д. На этом наборе мы строим матрицу размера 2N x N примерно такого вида:
| x1 | ... | xN — 1 | xN | |
| 0 | 0 | ... | 0 | 0 |
| 1 | 0 | ... | 0 | 1 |
| 2 | 0 | ... | 1 | 0 |
| ... | ||||
| 2N — 1 | 1 | ... | 1 | 1 |
Собственно, здесь каждый элемент обозначает простую вещь — проявляется или нет соответствующее значение xi. Как видно, строки матрицы помечены числами от 0 до 2N — 1, а в каждой строке мы имеем двоичное представление соответствующего числа. Именно поэтому процесс и назван бинаризацией.
Для всех строк указанной матрицы необходимо вычислить сводное значение и его вероятность. Сводное значение вычисляется как сумма тех значений, которым в данной строке соответствует 1. Ну а вероятность вычисляется как произведение вероятностей проявления или непроявления соответствующего значения. То есть, если в ячейке стоит 0, то соответствующим множителем будет (1 — pi), а если 1, то pi.
Перейдём к формулам. Вот формула для вычисления сводного значения, соответствующего строке i:
Формула (2): 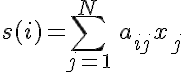
Напомню, что коэффициенты aij могут принимать значение 0 или 1. Соответственно, s(i) — это сумма тех значений, которые проявляются для данного i. Вероятность же для этого же i вычисляется по следующей формуле:
Формула (3): 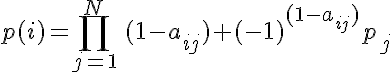
Здесь выражено то, что уже ранее написано словами — для тех значений, которые проявляются, берётся вероятность pj, а для тех, которые не проявляются, берётся, соответственно, (1 — pj).
В итоге у нас получается 2N пар (s(i), p(i)). Эти пары необходимо сгруппировать по первому элементу, то есть выделить группы, в которых s(i) одинаковый. Такие группы пар преобразуются в одну пару по следующей формуле:
Формула (4): 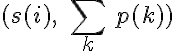
где s(i) — сводное значение, которое одинаково для всех пар этой группы, а аргумент вероятности k пробегает по всем индексам пар в группе. То есть мы просто суммируем вероятности для всех пар в группе, как бы схлопываем группу в одну пару.
Получив новый набор пар, нам остаётся выполнить следующие действия:
- Отсортировать набор пар по возрастанию первого элемента.
- Для отсортированного списка пар обновить вероятности (второй элемент) так, чтобы они шли «возрастающим итогом». Это значит, что нам надо к вероятности второго элемента пары прибавить вероятность первого элемента. К вероятности третьего элемента прибавить вероятности первого и второго и т. д. до конца, когда к вероятности последнего элемента должны быть добавлены вероятности всех предыдущих с закономерным итогом 1.
- Данный набор использовать для построения графика распределения вероятности значений рассматриваемого параметра.
- Использовать данный график для принятия решений.
Ну а решения можно применять примерно следующим образом. Пусть график построен, мы его видим перед собой. ЛПР может принять некий «порог допустимости», например, 70 %. Это будет нижний предел того, с какой вероятностью мы готовы рассматривать прогноз. Смотрим по графику, какое значение на оси абсцисс соответствует порогу в 70 %, отчерчиваем вертикальную линию и выбираем зону справа или зону слева от вертикальной черты для постановки задачи.
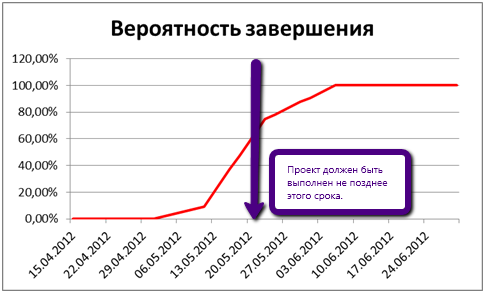
Но в целом описание механизма принятия решений по данному графику выходит за рамки данной статьи и будет рассмотрен когда-нибудь потом :).
Реализация на языке Haskell
Алгоритм описан. Давайте попробуем реализовать его на каком-нибудь хорошем языке программирования. Выберем для этих целей язык Haskell. На нём и напишем. Если же вы не очень сильны в программировании, то смело можете пропустить данный раздел статьи.
Начнём с определения модуля:
module Binarize
(
Item(..),
binarize
)
where
Определяем модуль Binarize, который экспортирует только две программные сущности — тип Item со всеми своими конструкторами, и функцию binarize. Что ж, идём дальше. Импортируем нужные модули и забираем из них только те функции, которые нам действительно пригодятся в работе:
import Control.Monad (replicateM)
import Data.Function (on)
import Data.List (groupBy, sortBy, inits)
Теперь перейдём к определениям типов данных. Как указано в интерфейсе модуля, нам надо определить тип Item. Других типов в этом модуле не будет. Данный тип Item является простой парой — при помощи него мы будем представлять пару (значение, вероятность). Можно было бы для этих использовать именно тип «пара» (с конструктором (,)), однако хорошим стилем программирования на языке Haskell является определение своих типов сразу к модификаторами:
data Item a b = Item
{
value :: a,
probability :: b
}
Как видно, данный тип полиморфен, причём параметризуется как тип значения value, так и тип для представления вероятности probability. Несмотря на то, что при реализации конкретных задач типовая переменная b наверняка примет значение Double, то есть число двойной точности с плавающей точкой, однако при определении типа Item надо оставлять для будущих пользователей модуля больше свободы. Ну а типовая переменная a сможет получить вообще произвольное значение — главное, чтобы их можно было сравнивать и складывать друг с другом, то есть это могут быть как целые числа, числа с плавающей точкой, комплексные числа, даты, даже строки. Посмотрим, как это выглядит в деле:
binarize :: (Num a, Ord a) => a -> [Item a Double] -> [Item a Double]
binarize g rs = map (addToValue g . sumProbabilities) $
tail $
inits $
map sumProbabilities $
groupBy ((==) `on` value) $
sortBy (compare `on` value) $
map (foldl sumItems (Item 0 1.0) . uncurry zip)
[(rs, ps) | ps <- replicateM (length rs) [False, True]]
Это и есть главная функция модуля, ради которой всё затевалось. Она получает на вход начальное значение исследуемого параметра, а также список прогнозных значений с приписанными к ним вероятностями. Как уже было сказано, вероятности представлены числом двойной точности с плавающей точкой. А вот значения могут быть представлены любым типом, только есть два ограничения — такие значения можно сравнивать (Ord) и складывать (Num).
Рассмотрение этой функции необходимо проводить с последней строки определения. В этой строке производится генерация списка. При помощи выражения replicateM (length rs) [False, True] генерируются все возможные комбинации значений True и False длиной, равной длине списка пар, поданных на вход функции binarize. Если, к примеру, у нас 2 пары на входе, то рассматриваемое выражение вернёт список [[False, False], [False, True], [True, False], [True, True]]. Это как раз то, что нам нужно (см. таблицу в предыдущем разделе), только мы будем использовать не числа 0 и 1, как в математической модели, а булевы значения истинности.
Итак, получили все возможные комбинации, после чего каждую из них соединили в пару с исходным списком пар вида (значение, вероятность). Получилось 2N элементов в новом списке. Далее к каждому элементу этого списка мы применяем волшебное выражение (foldl sumItems (Item 0 1.0) . uncurry zip). Рассмотрим подробнее, что оно делает. Функция zip принимает на вход два списка и возвращает список пар — первыми элементами пар являются элементы первого списка, а вторыми — второго, соответственно. Печаль в том, что у нас ей на вход будут подаваться пары, а она принимает не пары, а списки. Для этого мы саму функцию zip преобразуем в некаррированный вариант при помощи комбинатора uncurry. Что получилось? У нас была пара (rs, ps), а стал список [(r, p)]. И таких списков у нас образовалось ровно 2N (вспоминаем эффект функции map).
Другими словами, у нас теперь есть список пар, первым элементом которого является пара вида (значение, вероятность), а вторым — флаг проявления, то есть значение False (не проявляется) или True (проявляется). Всего таких списков, как уже сказано, у нас 2N по числу возможных комбинаций проявления или непроявления N прогнозных значений.
Далее к каждому такому списку применяется свёртка foldl при помощи функции sumItems и начального значения Item 0 1.0. Рассмотрим, что за функция sumItems такая:
sumItems :: (Num a, Num b) => Item a b -> (Item a b, Bool) -> Item a b
sumItems (Item v p) (Item v' p', False) = Item v (p * (1 - p'))
sumItems (Item v p) (Item v' p', True ) = Item (v + v') (p * p')
Эта функция реализует алгоритм складывания прогнозных значений с умножением их вероятностей. Тут производится получение одного прогнозного значения из списка пар вида ((значение, вероятность), флаг проявления). Если флаг проявления равен False, то соответствующее прогнозное значение не прибавляется к общей сумме, а вероятность умножается на вероятность непроявления, которая равна дополнению вероятности проявления до единицы. Ну а если флаг проявления равен True, то мы добавляем прогнозное значение к общей сумме, а вероятность умножаем на вероятность проявления, которая дана. Ну а начальное значение Item 0 1.0 для свёртки выбрано по простой причине — 0 является единицей для операции сложения, а 1.0 — единицей для операции умножения в соответствующих моноидах на числах.
Кстати, тут можно было бы использовать типы Sum и Product, являющиеся представлением соответствующих моноидов, но их использование очень сильно загромоздило бы определение, а гибкости не добавило бы (поскольку для этих моноидов нет определений для экземпляров классов Num и Ord, что крайне странно, — их пришлось бы писать самостоятельно).
Вернёмся к рассмотрению определения функции binarize. Итак, после применения ко всем элементам полученного после генерации списка свёртки, мы получаем список пар вида (значение, вероятность) из 2N элементов. Этот список содержит сводные прогнозные значения с соответствующими вероятностями, то есть каждый элемент данного списка соответствует одно строке из матрицы, но при этом значения и вероятности для каждой строки подсчитаны по известным формулам.
Далее сортируем этот список по значениям — это делает выражение sortBy (compare `on` value) — «сортируем, сравнивая по значениям». Отсортированный список мы группируем опять же по значению — это делает выражение groupBy ((==) `on` value) — «группируем, определяя на равенство по значениям». Получаем список списков. Для каждого элемента этого списка (а элементом является список) мы применяем функцию sumProbabilities, и вот её определение:
sumProbabilities :: [Item a Double] -> Item a Double
sumProbabilities = foldl1 ((Item v p) (Item v' p') -> Item v' (p + p'))
Это очень важная и интересная функция. Она сворачивает заданный список при помощи левоассоциативной свёртки, используя голову списка в качестве начального элемента (функция foldl1). Свёртка же осуществляется при помощи анонимной функции, которая в качестве прогнозного значения берёт значение из следующего сворачиваемого элемента, а вероятности просто суммируются. Очень важно здесь то, что в качестве значения в итоге получается последнее значение в сворачиваемом списке. Эта неявная логика была обнаружена в процессе разработки, и это поможет в дальнейшем. В первом же применении этой функции (которое рассматривается сейчас) то, какое значение берётся, не важно, поскольку все они одинаковые. Можно было бы написать анонимную функцию и так: ((Item v p) (Item v' p') -> Item v (p + p')), и в данном случае эффект был бы тот же.
Ну а после этого мы делаем небольшой финт ушами. Нам же теперь надо построить график, в котором вероятность будет считаться нарастающим итогом. Так что мы возьмём полученный список и применим к нему функцию inits. Она вернёт список списков из всех начал — сначала пустой список, потом список из головы, потом список из первого и второго элемента, и так далее до самого списка. Пустой список в начале нам не нужен, поэтому мы его отбросим при помощи функции tail. И вот тут нам опять помогает функция sumProbabilities, и то, что она в качестве прогнозного значения берёт последнее значение из списка, автоматически решает задачу — последнее значение и станет тем, для которого посчитается вероятность нарастающим итогом.
Ну и служебная функция addToValue определяется просто:
addToValue :: Num a => a -> Item a b -> Item a b
addToValue g (Item v p) = Item (v + g) p
Думаю, что её назначение понятно из определения :).
Итак, что мы имеем? Функция binarize осуществляет процесс бинаризации для заданного списка пар (значение, вероятность) и начального значения. Для этого она пользуется тремя служебными функциями. Функция sumItems реализует одновременно формулы (2) и (3). Функция sumProbabilities реализует формулу (4). Всё.
Заключение
В заключение хотелось бы поблагодарить всех читателей, осиливших данную статью до конца. Ну а если кто-то ещё напишет и комментарий с дельными замечаниями, то я вообще буду счастлив. Никто не уйдёт без ответа.
Если у вас или вашей компании есть интерес в более детальном изучении представленных методов, то я всегда готов к диалогу.
Ну а модуль, представленный в этой статье, вы можете получить здесь: Binarize.hs.
Мои предыдущие статьи по теме управления проектами на Хаброхабре:
- Методика управления рисками — обобщение моего опыта работы над проектами
- Апробация методики управления рисками: пять главных национальных рисков России
- Алгоритм построения графика распределения вероятности для объектов воздействия рисков
Автор: Darkus






