Главная

Гомоморфное шифрование своими руками

2012-08-23 в 5:41, admin, рубрики: Алгоритмы, Гомоморфное шифрование, информационная безопасность, криптография, метки: Гомоморфное шифрование, криптография

Доброго времени суток, уважаемые читатели. Те из вас кто интересуется криптографией наверняка знают, что такое гомоморфное шифрование и для чего оно нужно. Для тех кто пока не понимает о чем речь приведу определение из русскоязычной википедии:

Гомоморфное шифрование — криптографическая система, которая позволяет проводить определенные математические действия с открытым текстом путем произведения операций с зашифрованным текстом.

Долгое время полностью гомоморфная криптосистема оставалась для всех криптографов мира священным Граалем, недостижимым идеалом. И вот в 2009 году Craig Gentry в своей диссертации впервые описал полностью рабочую схему гомоморфного шифрования.
Несколько математических подробностей идеи Gentry а также пример реализации его алгоритма вы найдете под катом.

Гомоморфное шифрование.

Любую стандартную систему шифрования можно описать тремя алгоритмами.

Генерация ключей KeyGen()
Шифрование Encypt()
Расшифровка Decrypt()

Гомоморфная криптосистема помимо трех вышеперечисленных алгоритмов включает в себя алгоритм вычислений Eval().
Схематично алгоритм Eval можно представить следующим образом:
Гомоморфное шифрование своими руками
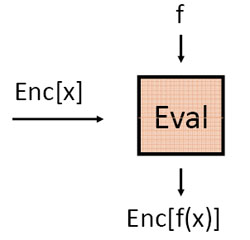
На вход алгоритму подается зашифрованное сообщение Enc(M) и некая математическая функция f(). Результатом работы алгоритма является другое зашифрованное сообщение Enc(M₂), причем M₂=f(M).

Схема гомоморфного шифрования считается корректной если для любой пары ключей SK, PK, для любой функции f(), для любого набора шифротекстов С={c₁,c₂,..,c_n} и любого набора открытых текстов {m₁,m₂,..,m_n} выполняется следующее условие:
Если r=Eval(PK,C,f) тогда decypt(SK,r)=f(m₁,m₂,..,m_n)
Схема предложенная Gentry соответствует данному условию и поэтому ее можно назвать полностью гомоморфной.

Схема Gentry с числами

Опишем саму схему шифрования применимую для данных представленных в числовом виде.
KeyGen
Закрытый ключ: большое четное число N.
Открытый ключ: набор больших чисел {a₁,a₂,..,a_i} таких что a_i mod N=2e_i, где e_i числа намного меньше N.
Encrypt
Из открытого ключа генерируем случайное число b=random-subset-sum{a_i}. Для того чтобы зашифровать 1 бит информации m ∈{0,1} вычислим
С=b+m
Decrypt
Для расшифровки вычислим
С mod N=m+2*Пe_i
2*Пe_i называют шумом, если данное выражение в процессе вычислений станет больше числа N, то расшифровка будет невозможна.
После приведения по модулю два получим исходное сообщение m.
Eval
Чтобы произвести сложение или умножение зашифрованных элементов не расшифровывая их, достаточно просто сложить или умножить шифротексты.
Несмотря на то что эта схема является абсолютно рабочей, она представляет не очень большой интерес, т.к. с ее помощью можно зашифровать только 1 бит информации. Для того чтобы работать с большими числами немного видоизменим алгоритм.
Построим схему, которая бы позволяла нам шифровать числа не больше 15.
KeyGen
Закрытый ключ: большое число N, такое что НОД(N,15)=1.
Открытый ключ: набор больших чисел {a₁,a₂,..,a_i} таких что a_i mod N=15e_i, где e_i числа намного меньше N.
Encrypt
Из открытого ключа генерируем случайное число b=random-subset-sum{a_i}. Для того чтобы зашифровать число от 0 до 15 вычислим
С=b+m
Decrypt
Для расшифровки вычислим
С mod N=m+15*Пe_i
После приведения по модулю 15 получим исходное сообщение m.

Реализация на C#

Ниже приведена часть кода, содержащая функции генерации ключей, шифрования и дешифрования.

        //функция генерации ключей, переменная k-максимальное значение числа 
        //с которым может работать криптосистема
        private BigInteger[] PublicKeyGenerate(BigInteger N, int k)
        {
            Random r = new Random();
            byte[] rand = new byte[16];
            BigInteger rem;
            for (int i = 0; i < 100; i++)
            {
                    r.NextBytes(rand);
                    PK[i] = new BigInteger(rand);
                    PK[i] = (BigInteger.Abs(PK[i]) * N) + (k* r.Next(10, 100));
                    rem = BigInteger.Remainder(PK[i], N);;
            }
            return PK;
        }
        //функция шифрования, параметрами служат
        // открытый текст M и Открытый ключ PK
        private BigInteger Encryption(BigInteger M, BigInteger[] PK)
        {
            BigInteger B = new BigInteger(0);
            BigInteger C = new BigInteger(0);
            Random r = new Random();
            for (int i = 0; i < 100; i++)
            {
                if (r.Next(2) == 1)
                    B = B + PK[i];
            }
            C = M + B;
            return C;
        }
        //функция дешифровки, C-шифротекст, N-закрытый ключ, 
        //k-максимально допустимое значение открытого текста
        private BigInteger Decryption(BigInteger C, BigInteger N, int k)
        {
            BigInteger M = new BigInteger(0);
            M = BigInteger.Remainder(C, N);
            return BigInteger.Remainder(M, k);
        }

Скачать исходники программки реализующей шифрование чисел до 1000 можно отсюда.

Заключение

В заключение стоит отметить, что описанная в данном топики криптосистема не более чем прототип, основным предназначением которого является ознакомить интересующихся с принципом работы гомоморфной криптосистемы. Реальные гомоморфные схемы работают не с целыми числами, а с кольцами полиномов, и в них после каждого вычисления производят приведение по модулю, чтобы снизить шум и не сделать расшифровку невозможной.