 Недавно мне понадобилось написать 2-3-дерево и я начал искать информацию в русскоязычном интернете. К сожалению, ни на хабре, ни на других ресурсах я не смог найти достаточно полную информацию на русском языке. На всех ресурсах было одно и то же: свойства дерева, как вставляются ключи в дерево, поиск в дереве и иногда простой пример, как удаляется ключ из дерева; не было реализации.
Недавно мне понадобилось написать 2-3-дерево и я начал искать информацию в русскоязычном интернете. К сожалению, ни на хабре, ни на других ресурсах я не смог найти достаточно полную информацию на русском языке. На всех ресурсах было одно и то же: свойства дерева, как вставляются ключи в дерево, поиск в дереве и иногда простой пример, как удаляется ключ из дерева; не было реализации.
Поэтому, после того, как я сделал то, что мне нужно, решил написать данную статью. Думаю, кому-нибудь будет полезна в образовательных целях, так как на практике обычно реализуют эквивалент 2-3- и 2-3-4-деревьев — красно-черное дерево.
Вводная часть
Те, кто знают, что такое двоичное дерево поиска и его недостатки, могут листать дальше — ничего нового здесь не будет.
Большинству программистов (и не только) известно такое дерево как бинарное дерево поиска. У этого дерева очень простые свойства:
- Оба поддерева — левое и правое — являются двоичными деревьями поиска.
- У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
- В то время, как значения ключей данных у всех узлов правого поддерева (того же узла X) больше либо равно, нежели значение ключа данных узла X.
Деревья поиска используют тогда, когда нужно очень часто выполнять операцию поиск. В обычном дереве поиска есть очень большой недостаток: когда на вход получаем отсортированные данные, наше дерево становится обычным массивом:

И тогда операция поиск будет осуществляться за такую же сложность, как и в массиве, — за O(n), где n — количество элементов в массиве.
Есть несколько способов, как можно обычное дерево сделать сбалансированным (поиск имеет сложность O(log n)). Об этом очень хорошо написано в двух статьях от читателя nickme: рандомизированные деревья поиска и АВЛ-деревья.
Общие свойства 2-3-дерева
Определение из wiki:
2-3-дерево — структура данных, являющаяся B-деревом Степени 1, страницы которого могут содержать только 2-вершины (вершины с одним полем и 2 детьми) и 3-вершины (вершины с 2 полями и 3 детьми). Листовые вершины являются исключением — у них нет детей (но может быть одно или два поля). 2-3-деревья сбалансированы, то есть, каждое левое, правое, и центральное поддерево имеет одну и ту же высоту, и, таким образом, содержат равные (или почти равные) объемы данных.
Свойства:
- Все нелистовые вершины содержат одно поле и 2 поддерева или 2 поля и 3 поддерева.
- Все листовые вершины находятся на одном уровне (на нижнем уровне) и содержат 1 или 2 поля.
- Все данные отсортированы (по принципу двоичного дерева поиска).
- Нелистовые вершины содержат одно или два поля, указывающие на диапазон значений в их поддеревьях. Значение первого поля строго больше наибольшего значения в левом поддереве и меньше или равно наименьшему значению в правом поддереве (или в центральном поддереве, если это 3-вершина); аналогично, значение второго поля (если оно есть) строго больше наибольшего значения в центральном поддереве и меньше или равно, чем наименьшее значение в правом поддереве. Эти нелистовые вершины используются для направления функции поиска к нужному поддереву и, в конечном итоге, к нужному листу. (прим. Это свойство не будет выполняться, если у нас есть одинаковые ключи. Поэтому возможна ситуация, когда равные ключи находятся в левом и правом поддеревьях одновременно, тогда ключ в нелистовой вершине будет совпадать с этими ключами. Это никак не сказывается на правильности работы и производительности алгоритма.).
Пример 2-3-дерева:
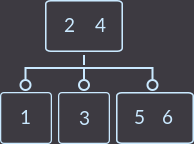
Для простоты будем использовать различные ключи
Представление дерева в коде
Я буду писать на так называемом «Си с классами», так как я сам программист на Си, но мне безумно нравятся такие вещи в С++, как конструкторы, наличие членов-методов класса и дружественные функции.
Вершины нашего дерева будем представлять в виде 4-вершин (это когда вершина может иметь 3 ключа и 4 сына). Данное решение было выбрано по нескольким причинам: во-первых, так легче сделать наивную (прямую) реализацию, а во-вторых, код и так сильно обрамлен if'ами и это решение позволило уменьшить количество проверок и упростить код.
Вот так выглядит представление вершины:
struct node {
private:
int size; // количество занятых ключей
int key[3];
node *first; // *first <= key[0];
node *second; // key[0] <= *second < key[1];
node *third; // key[1] <= *third < key[2];
node *fourth; // kye[2] <= *fourth.
node *parent; //Указатель на родителя нужен для того, потому что адрес корня может меняться при удалении
bool find(int k) { // Этот метод возвращает true, если ключ k находится в вершине, иначе false.
for (int i = 0; i < size; ++i)
if (key[i] == k) return true;
return false;
}
void swap(int &x, int &y) {
int r = x;
x = y;
y = r;
}
void sort2(int &x, int &y) {
if (x > y) swap(x, y);
}
void sort3(int &x, int &y, int &z) {
if (x > y) swap(x, y);
if (x > z) swap(x, z);
if (y > z) swap(y, z);
}
void sort() { // Ключи в вершинах должны быть отсортированы
if (size == 1) return;
if (size == 2) sort2(key[0], key[1]);
if (size == 3) sort3(key[0], key[1], key[2]);
}
void insert_to_node(int k) { // Вставляем ключ k в вершину (не в дерево)
key[size] = k;
size++;
sort();
}
void remove_from_node(int k) { // Удаляем ключ k из вершины (не из дерева)
if (size >= 1 && key[0] == k) {
key[0] = key[1];
key[1] = key[2];
size--;
} else if (size == 2 && key[1] == k) {
key[1] = key[2];
size--;
}
}
void become_node2(int k, node *first_, node *second_) { // Преобразовать в 2-вершину.
key[0] = k;
first = first_;
second = second_;
third = nullptr;
fourth = nullptr;
parent = nullptr;
size = 1;
}
bool is_leaf() { // Является ли узел листом; проверка используется при вставке и удалении.
return (first == nullptr) && (second == nullptr) && (third == nullptr);
}
public:
// Создавать всегда будем вершину только с одним ключом
node(int k): size(1), key{k, 0, 0}, first(nullptr), second(nullptr),
third(nullptr), fourth(nullptr), parent(nullptr) {}
node (int k, node *first_, node *second_, node *third_, node *fourth_, node *parent_):
size(1), key{k, 0, 0}, first(first_), second(second_),
third(third_), fourth(fourth_), parent(parent_) {}
friend node *split(node *item); // Метод для разделение вершины при переполнении;
friend node *insert(node *p, int k); // Вставка в дерево;
friend node *search(node *p, int k); // Поиск в дереве;
friend node *search_min(node *p); // Поиск минимального элемента в поддереве;
friend node *merge(node *leaf); // Слияние используется при удалении;
friend node *redistribute(node *leaf); // Перераспределение также используется при удалении;
friend node *fix(node *leaf); // Используется после удаления для возвращения свойств дереву (использует merge или redistribute)
friend node *remove(node *p, int k); // Собственно, из названия понятно;
};
Вставка
Для того, чтобы вставить в дерево элемент с ключом key, нужно действовать по алгоритму:
- Если дерево пусто, то создать новую вершину, вставить ключ и вернуть в качестве корня эту вершину, иначе
- Если вершина является листом, то вставляем ключ в эту вершину и если получили 3 ключа в вершине, то разделяем её, иначе
- Сравниваем ключ key с первым ключом в вершине, и если key меньше данного ключа, то идем в первое поддерево и переходим к пункту 2, иначе
- Смотрим, если вершина содержит только 1 ключ (является 2-вершиной), то идем в правое поддерево и переходим к пункту 2, иначе
- Сравниваем ключ key со вторым ключом в вершине, и если key меньше второго ключа, то идем в среднее поддерево и переходим к пункту 2, иначе
- Идем в правое поддерево и переходим к пункту 2.
Для примера вставим keys = {1, 2, 3, 4, 5, 6, 7}:
При вставке key=1 мы имеем пустое дерево, а после получаем единственную вершину с единственным ключа key=1:

Дальше вставляем key=2:

Теперь вставляем key=3 и получаем вершину, содержащую 3 ключа:

Так как эта вершина нарушает свойства 2-3-дерева, то мы должны с этим разобраться. А разберемся с этим вот таким разделением: ключ, который находится в середине (в нашем случае key=2), перенесем в родительскую вершину на соответствующее место, либо если у нас единственная вершина в дереве, то она соответственно является и корнем дерева — значит, мы создаем новую вершину и переносим туда средний ключ key = 2, а остальные ключи сортируем и делаем их сыновьями нового корня:
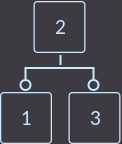
Дальше по алгоритму вставляем key=4:
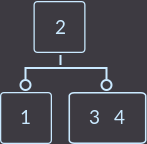
Key=5:
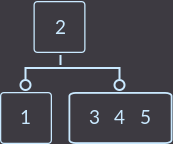
Снова нарушилось свойства 2-3 дерева, делаем разделение:
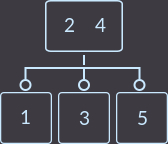
Key=6:
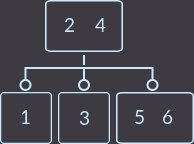
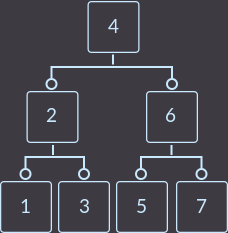
Key=7:
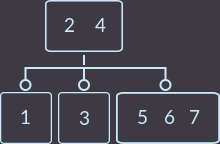
Теперь нам предстоит сделать два разделения, т.к. вершина, в которую вставили новый ключ теперь имеет 3 ключа (сначала разделим ее):
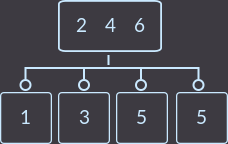
А теперь и корень имеет 3 вершины — разделим его и получим сбалансированное дерево, которое при таких входных данных с обычным двоичным деревом поиска мы бы не смогли получить:
node *insert(node *p, int k) { // вставка ключа k в дерево с корнем p; всегда возвращаем корень дерева, т.к. он может меняться
if (!p) return new node(k); // если дерево пусто, то создаем первую 2-3-вершину (корень)
if (p->is_leaf()) p->insert_to_node(k);
else if (k <= p->key[0]) insert(p->first, k);
else if ((p->size == 1) || ((p->size == 2) && k <= p->key[1])) insert(p->second, k);
else insert(p->third, k);
return split(p);
}
node *split(node *item) {
if (item->size < 3) return item;
node *x = new node(item->key[0], item->first, item->second, nullptr, nullptr, item->parent); // Создаем две новые вершины,
node *y = new node(item->key[2], item->third, item->fourth, nullptr, nullptr, item->parent); // которые имеют такого же родителя, как и разделяющийся элемент.
if (x->first) x->first->parent = x; // Правильно устанавливаем "родителя" "сыновей".
if (x->second) x->second->parent = x; // После разделения, "родителем" "сыновей" является "дедушка",
if (y->first) y->first->parent = y; // Поэтому нужно правильно установить указатели.
if (y->second) y->second->parent = y;
if (item->parent) {
item->parent->insert_to_node(item->key[1]);
if (item->parent->first == item) item->parent->first = nullptr;
else if (item->parent->second == item) item->parent->second = nullptr;
else if (item->parent->third == item) item->parent->third = nullptr;
// Дальше происходит своеобразная сортировка ключей при разделении.
if (item->parent->first == nullptr) {
item->parent->fourth = item->parent->third;
item->parent->third = item->parent->second;
item->parent->second = y;
item->parent->first = x;
} else if (item->parent->second == nullptr) {
item->parent->fourth = item->parent->third;
item->parent->third = y;
item->parent->second = x;
} else {
item->parent->fourth = y;
item->parent->third = x;
}
node *tmp = item->parent;
delete item;
return tmp;
} else {
x->parent = item; // Так как в эту ветку попадает только корень,
y->parent = item; // то мы "родителем" новых вершин делаем разделяющийся элемент.
item->become_node2(item->key[1], x, y);
return item;
}
}
Поиск
Поиск такой же простой, как и в бинарном дереве поиска:
- Ищем искомый ключ key в текущей вершине, если нашли, то возвращаем вершину, иначе
- Если key меньше первого ключа вершины, то идем в левое поддерево и переходим к пункту 1, иначе
- Если в дереве 1 ключ, то идем в правое поддерево (среднее, если руководствоваться нашим классом) и переходим к пункту 1, иначе
- Если key меньше второго ключа вершины, то идем в среднее поддерево и переходим к пункту 1, иначе
- Идем в правое поддерево и переходим к пункту 1.
node *search(node *p, int k) { // Поиск ключа k в 2-3 дереве с корнем p.
if (!p) return nullptr;
if (p->find(k)) return p;
else if (k < p->key[0]) return search(p->first, k);
else if ((p->size == 2) && (k < p->key[1]) || (p->size == 1)) return search(p->second, k);
else if (p->size == 2) return search(p->third, k);
}
Удаление
Удаление в 2-3-дереве, как и в любом другом дереве, происходит только из листа (из самой нижней вершины). Поэтому, когда мы нашли ключ, который нужно удалить, сначала надо проверить, находится ли этот ключ в листовой или нелистовой вершине. Если ключ находится в нелистовой вершине, то нужно найти эквивалентный ключ для удаляемого ключа из листовой вершины и поменять их местами. Для нахождения эквивалентного ключа есть два варианта: либо найти максимальный элемент в левом поддереве, либо найти минимальный элемент в правом поддереве. Давайте выберем второй вариант, так как он мне больше нравится. Например:
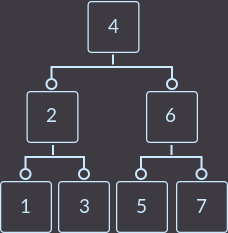
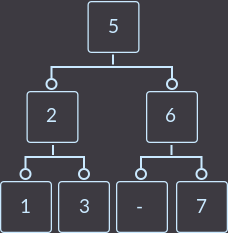
Чтобы удалить из дерева ключ key=4, для начала нужно найти эквивалентный эму элемент и поменять местами: это либо key=3, либо key=5. Так как я выбрал второй способ, то меняю ключи key=4 и key=5 местами и удаляю key=4 из листа («тире» будет обозначать место ключа, который мы удалили):
node *search_min(node *p) { // Поиск узла с минимальным элементов в 2-3-дереве с корнем p.
if (!p) return p;
if (!(p->first)) return p;
else return search_min(p->first);
}
node *remove(node *p, int k) { // Удаление ключа k в 2-3-дереве с корнем p.
node *item = search(p, k); // Ищем узел, где находится ключ k
if (!item) return p;
node *min = nullptr;
if (item->key[0] == k) min = search_min(item->second); // Ищем эквивалентный ключ
else min = search_min(item->third);
if (min) { // Меняем ключи местами
int &z = (k == item->key[0] ? item->key[0] : item->key[1]);
item->swap(z, min->key[0]);
item = min; // Перемещаем указатель на лист, т.к. min - всегда лист
}
item->remove_from_node(k); // И удаляем требуемый ключ из листа
return fix(item); // Вызываем функцию для восстановления свойств дерева.
}
После того, как удалили ключ, у нас могут получиться концептуально 4 разные ситуации: 3 из них нарушают свойства дерева, а одна — нет. Поэтому для вершины, из которой удалили ключ, нужно вызвать функцию исправления fix(), которая вернет свойства 2-3 дерева. Случаи, которые описываются в функции, рассматриваются ниже.
node *fix(node *leaf) {
if (leaf->size == 0 && leaf->parent == nullptr) { // Случай 0, когда удаляем единственный ключ в дереве
delete leaf;
return nullptr;
}
if (leaf->size != 0) { // Случай 1, когда вершина, в которой удалили ключ, имела два ключа
if (leaf->parent) return fix(leaf->parent);
else return leaf;
}
node *parent = leaf->parent;
if (parent->first->size == 2 || parent->second->size == 2 || parent->size == 2) leaf = redistribute(leaf); // Случай 2, когда достаточно перераспределить ключи в дереве
else if (parent->size == 2 && parent->third->size == 2) leaf = redistribute(leaf); // Аналогично
else leaf = merge(leaf); // Случай 3, когда нужно произвести склеивание и пройтись вверх по дереву как минимум на еще одну вершину
return fix(leaf);
}
Теперь перейдем к возможным вариантам, которые могут появиться после удаления ключа. Для простоты будем рассматривать случаи, где глубина дерева равна 2. Общий случай — это дерево с глубиной равной трем. Тогда будет понятно, как справиться с удалением ключа в дереве с любой глубиной. Что мы и сделаем в итоговом примере для большинства ситуаций. А пока приступим к частным случаям.
Случай 0:
Самый простой случай, также как и следующий, на которые хватит и одного предложения, чтобы понять: если дерево состоит из одной вершины (корень), которая имеет 1 ключ, то просто удаляем эту вершину. The end.
Случай 1:
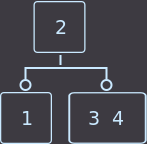
Если нужно удалить ключ из листа, где находятся два ключа, то мы просто удаляем ключ и на этом функция удаления закончена.
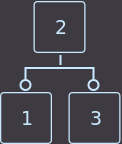
Удалим key=4:
 ->
-> 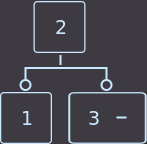 ->
-> 
Случай 2 (распределение или redistribute):
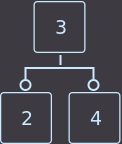
Мы удаляем ключ из вершины и вершина становится пустой. Если хотя бы у одного из братьев есть 2 ключа, то делаем простое правильное распределение и работа закончена. Под правильным распределением я подразумеваю, что при при цикличном сдвиге ключей между родителем и сыновьями также нужно будет перемещать и внуков родителя. Перераспределять ключи можно из любого брата, но удобнее всего из ближнего, который имеет 2 ключа, при этом мы циклично сдвигаем все ключи, например из примера ниже удалим key=1:
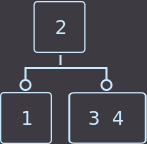 ->
->  ->
-> 
Или вот второй пример: у нас родитель имеет 2 ключа, соответственно 3 сына, и мы удалим key=4. Перераспределение в нашем примере можно сделать как из левого брата, так и из правого; я выбрал из левого:
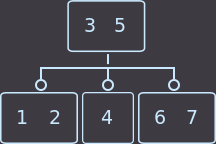 ->
-> 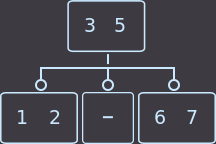 ->
-> 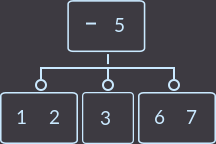 ->
-> 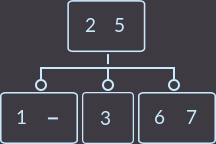 ->
->
-> 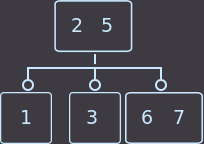
Как видим, свойства дерева сохранены.
node *redistribute(node *leaf) {
node *parent = leaf->parent;
node *first = parent->first;
node *second = parent->second;
node *third = parent->third;
if ((parent->size == 2) && (first->size < 2) && (second->size < 2) && (third->size < 2)) {
if (first == leaf) {
parent->first = parent->second;
parent->second = parent->third;
parent->third = nullptr;
parent->first->insert_to_node(parent->key[0]);
parent->first->third = parent->first->second;
parent->first->second = parent->first->first;
if (leaf->first != nullptr) parent->first->first = leaf->first;
else if (leaf->second != nullptr) parent->first->first = leaf->second;
if (parent->first->first != nullptr) parent->first->first->parent = parent->first;
parent->remove_from_node(parent->key[0]);
delete first;
} else if (second == leaf) {
first->insert_to_node(parent->key[0]);
parent->remove_from_node(parent->key[0]);
if (leaf->first != nullptr) first->third = leaf->first;
else if (leaf->second != nullptr) first->third = leaf->second;
if (first->third != nullptr) first->third->parent = first;
parent->second = parent->third;
parent->third = nullptr;
delete second;
} else if (third == leaf) {
second->insert_to_node(parent->key[1]);
parent->third = nullptr;
parent->remove_from_node(parent->key[1]);
if (leaf->first != nullptr) second->third = leaf->first;
else if (leaf->second != nullptr) second->third = leaf->second;
if (second->third != nullptr) second->third->parent = second;
delete third;
}
} else if ((parent->size == 2) && ((first->size == 2) || (second->size == 2) || (third->size == 2))) {
if (third == leaf) {
if (leaf->first != nullptr) {
leaf->second = leaf->first;
leaf->first = nullptr;
}
leaf->insert_to_node(parent->key[1]);
if (second->size == 2) {
parent->key[1] = second->key[1];
second->remove_from_node(second->key[1]);
leaf->first = second->third;
second->third = nullptr;
if (leaf->first != nullptr) leaf->first->parent = leaf;
} else if (first->size == 2) {
parent->key[1] = second->key[0];
leaf->first = second->second;
second->second = second->first;
if (leaf->first != nullptr) leaf->first->parent = leaf;
second->key[0] = parent->key[0];
parent->key[0] = first->key[1];
first->remove_from_node(first->key[1]);
second->first = first->third;
if (second->first != nullptr) second->first->parent = second;
first->third = nullptr;
}
} else if (second == leaf) {
if (third->size == 2) {
if (leaf->first == nullptr) {
leaf->first = leaf->second;
leaf->second = nullptr;
}
second->insert_to_node(parent->key[1]);
parent->key[1] = third->key[0];
third->remove_from_node(third->key[0]);
second->second = third->first;
if (second->second != nullptr) second->second->parent = second;
third->first = third->second;
third->second = third->third;
third->third = nullptr;
} else if (first->size == 2) {
if (leaf->second == nullptr) {
leaf->second = leaf->first;
leaf->first = nullptr;
}
second->insert_to_node(parent->key[0]);
parent->key[0] = first->key[1];
first->remove_from_node(first->key[1]);
second->first = first->third;
if (second->first != nullptr) second->first->parent = second;
first->third = nullptr;
}
} else if (first == leaf) {
if (leaf->first == nullptr) {
leaf->first = leaf->second;
leaf->second = nullptr;
}
first->insert_to_node(parent->key[0]);
if (second->size == 2) {
parent->key[0] = second->key[0];
second->remove_from_node(second->key[0]);
first->second = second->first;
if (first->second != nullptr) first->second->parent = first;
second->first = second->second;
second->second = second->third;
second->third = nullptr;
} else if (third->size == 2) {
parent->key[0] = second->key[0];
second->key[0] = parent->key[1];
parent->key[1] = third->key[0];
third->remove_from_node(third->key[0]);
first->second = second->first;
if (first->second != nullptr) first->second->parent = first;
second->first = second->second;
second->second = third->first;
if (second->second != nullptr) second->second->parent = second;
third->first = third->second;
third->second = third->third;
third->third = nullptr;
}
}
} else if (parent->size == 1) {
leaf->insert_to_node(parent->key[0]);
if (first == leaf && second->size == 2) {
parent->key[0] = second->key[0];
second->remove_from_node(second->key[0]);
if (leaf->first == nullptr) leaf->first = leaf->second;
leaf->second = second->first;
second->first = second->second;
second->second = second->third;
second->third = nullptr;
if (leaf->second != nullptr) leaf->second->parent = leaf;
} else if (second == leaf && first->size == 2) {
parent->key[0] = first->key[1];
first->remove_from_node(first->key[1]);
if (leaf->second == nullptr) leaf->second = leaf->first;
leaf->first = first->third;
first->third = nullptr;
if (leaf->first != nullptr) leaf->first->parent = leaf;
}
}
return parent;
}
Случай 3 (склеивание или merge):
Пожалуй, самый сложный случай, так как после склеивания всегда обязательно идти по дереву вверх и опять применять операции либо merge, либо redistribute. После redistribute алгоритм восстановления свойств 2-3-дерева после удаления ключа можно прекратить, так как вершины в этой операции не удаляются.
Для начала посмотрим, как удалить ключ key=3 из вершины, родитель которой имеет только двух сыновей (~ 1 ключ):
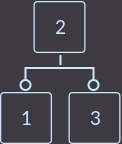 ->
-> 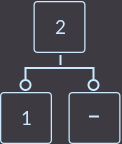 ->
-> 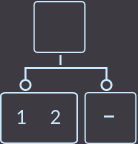 ->
-> 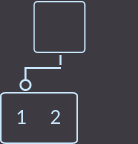 ->
-> 
Что же мы сделали? Мы удалили ключ key=3. Затем нам нужно перенести ключ из родителя в того сына, где ключ есть: в данном случае в левого сына. Затем нужно удалить вершину, из которой удалили ключ. И последний шаг — это проверить, если родитель был корнем дерева, то удалить этот корень и назначить новый корнем ту вершину, куда мы перенесли ключ, иначе придется вызывать функцию исправления fix() уже для родителя. Выглядит легко.
Теперь рассмотрим два варианта, когда родитель имеет 2 ключа. В первом варианте удалим key=3 (из среднего сына):
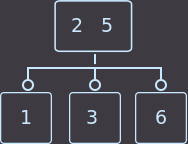 ->
-> 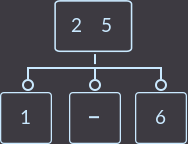 ->
-> 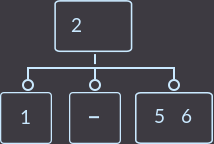 ->
-> 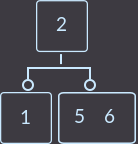
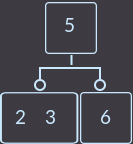
Что мы сделали на этот раз? Мы снова перенесли ключ родителя (уже один из двух) к сыну и удалили сына, который не имеет ключей. Так как родитель имел 2 ключа, то проверять, являлся ли родитель корнем, не нужно. В описанном выше случае алгоритм исправления такой: нужно перенести меньший ключ родителя в поддерево с меньшими ключами либо больший ключ в поддерево с большими ключами, и удалить вершину без ключей. Еще пример, удалим key=1:
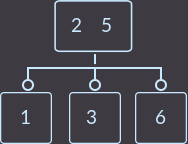 ->
-> 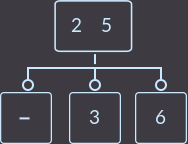 ->
-> 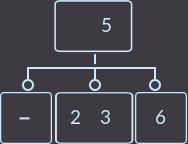 ->
-> 
node *merge(node *leaf) {
node *parent = leaf->parent;
if (parent->first == leaf) {
parent->second->insert_to_node(parent->key[0]);
parent->second->third = parent->second->second;
parent->second->second = parent->second->first;
if (leaf->first != nullptr) parent->second->first = leaf->first;
else if (leaf->second != nullptr) parent->second->first = leaf->second;
if (parent->second->first != nullptr) parent->second->first->parent = parent->second;
parent->remove_from_node(parent->key[0]);
delete parent->first;
parent->first = nullptr;
} else if (parent->second == leaf) {
parent->first->insert_to_node(parent->key[0]);
if (leaf->first != nullptr) parent->first->third = leaf->first;
else if (leaf->second != nullptr) parent->first->third = leaf->second;
if (parent->first->third != nullptr) parent->first->third->parent = parent->first;
parent->remove_from_node(parent->key[0]);
delete parent->second;
parent->second = nullptr;
}
if (parent->parent == nullptr) {
node *tmp = nullptr;
if (parent->first != nullptr) tmp = parent->first;
else tmp = parent->second;
tmp->parent = nullptr;
delete parent;
return tmp;
}
return parent;
}
! Важно! При склеивании или перераспределении нелистовой вершины нужно будет также склеивать и/или перераспределять сыновей братьев.
Итоговый пример удаления ключей:
Подобрал пример такой, чтобы можно было увидеть все основные случаи (кроме случая 0). Для начала вставим ключи keys={10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 5, 15, 25, 8} в пустое дерево и получим:
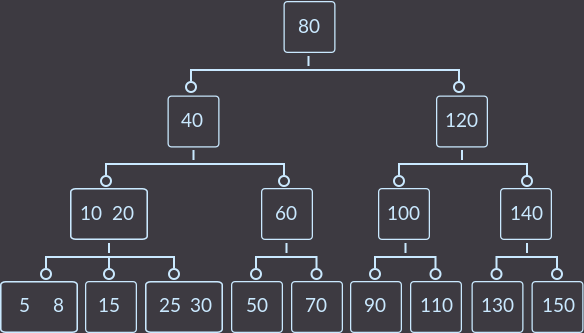
Теперь удалим по порядку ключи keys={5, 8, 10, 30, 15}.
После удаления ключа key=5 получаем:
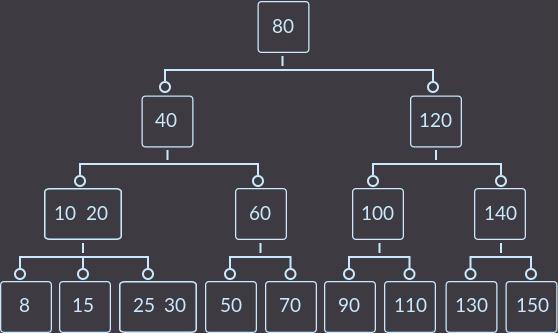
Удаляем key=8:
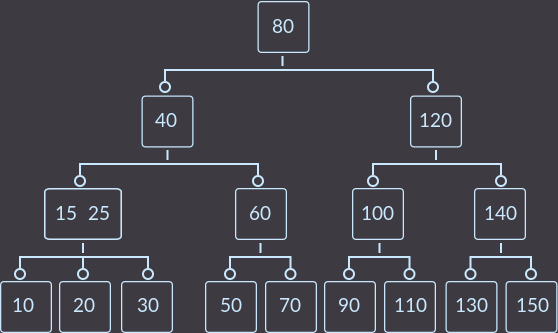
Теперь key=10:
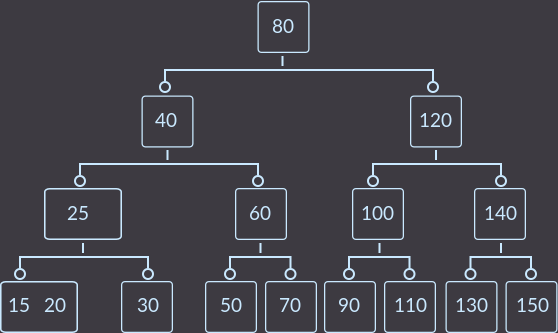
Key=30:
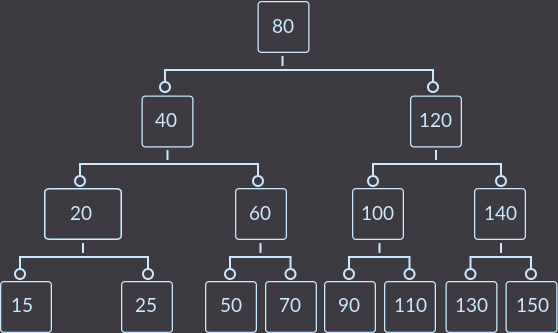
И, наконец, key=15. Так как тут происходит при исправлении дерева операция merge, то посмотрим на все шаги.
Шаг 1. Вид дерева сразу после первого вызова fix():
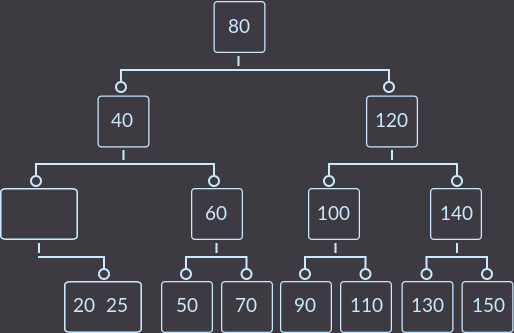
Шаг 2. Второй вызов fix():
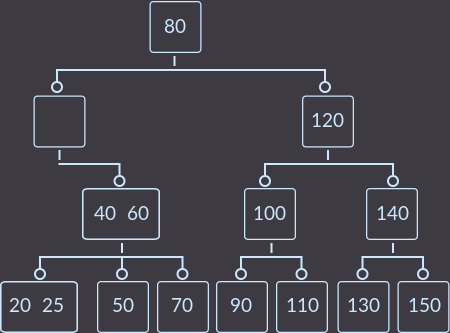
Шаг 3. Третий вызов fix():
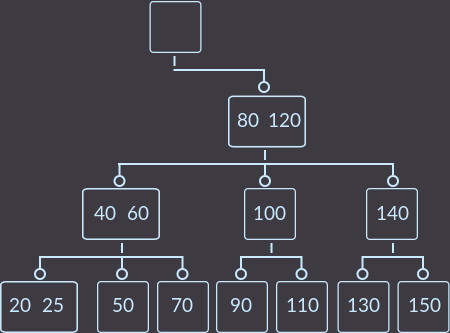
Шаг 4. Последний вызов fix():
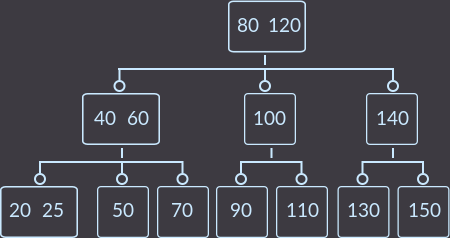
Вот так мы удалили ключ key=15 и дерево осталось с теми свойствами, с которыми и должно быть.
На этом всё, спасибо за внимание.
Автор: konshyn



