В предыдущей статье я рассказал теоретическое обоснование копул. Так как сам был студентом, знаю, что лучшим объяснением теоретического аппарата может служить пример его практического применения. Поэтому в этой статье попробую показать, как копулы используются для моделирования взаимозависимостей нескольких случайных величин.

Опять немного теории
Как уже упоминалось, многие копулы могут отражать зависимость не только двух, но сразу нескольких величин. Это, конечно, хорошо, но стандартные копулы подразумевают некоторую симметричность, то есть все попарные зависимости будут иметь одинаковый паттерн. Согласитесь, это не всегда является правдой. Для преодоления этой проблемы был предложен интересный и вполне очевидный (сколько мучений скрыто за этим словом в математическом анализе) способ – мы разбиваем совместную копулу на набор двумерных копул. Мы знаем, что для n переменных у нас будет 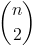 попарных взаимосвязей. То есть нам придется определить именно столько попарных копул. Покажем, что совместную плотность распределения 4 величин можно выразить следующим образом:
попарных взаимосвязей. То есть нам придется определить именно столько попарных копул. Покажем, что совместную плотность распределения 4 величин можно выразить следующим образом:
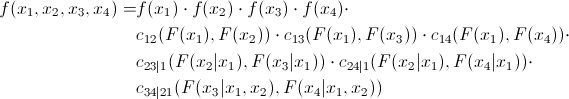
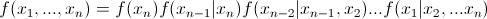
Так же из определения копулы, мы знаем, что:
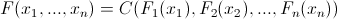
что в свою очередь можно выразить следующим образом:
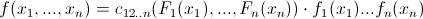
Для двумерного случая это будет выглядеть следующим образом:
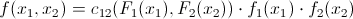
И совместив это с самой первой формулой, мы получаем:
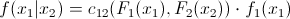
Можно расширить этот пример до трехмерного случая:
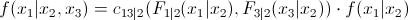
и совместив с предыдущей формулой, мы получаем:
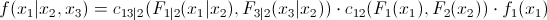
Таким образом, мы видим, что все элементы из первого уравнения могут быть представлены в виде произведения парных копул и маржинальной плотности.
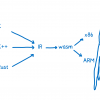
Существует несколько способов представления разбиения, и упомянутый выше называется канонической лозой (искренне прошу прощения, но устоявшегося перевода «canonical vine» в математическом контексте я не нашёл, так что буду использовать прямой перевод). Графически последнее уравнение можно представить следующим образом:
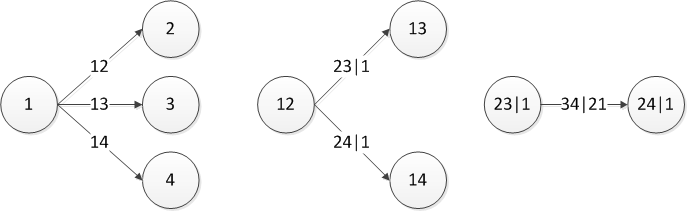
Три дерева описывают разбиение 4-мерной копулы. В самом левом дереве кружки – это маржинальные распределения, стрелки – двухмерные копулы. Наша задача, как человека ответственного за моделирование – задать все «стрелки», то есть определить попарные копулы и их параметры.
Теперь посмотрим на формулу D-образной лозы:
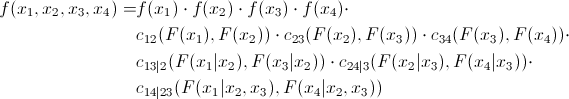
и ее графическое представление
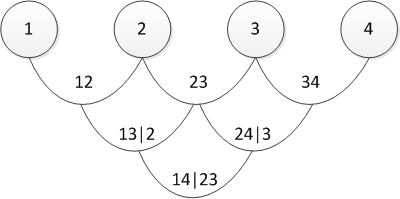
По сути, каноническая и D-лозы отличаются только порядком определения попарных зависимостей. Можно задаться вопросом — «а как я буду выбирать порядок?» или эквивалентный «а какую лозу мне выбирать?» На это есть ответ у меня: на практике начинают с пар, которые показывают наибольшую взаимосвязь. Последнюю определяют по тау Кендалла. Не волнуйтесь — все станет яснее позже, когда я буду показывать непосредственный практический пример.
После того, как вы определились с порядком определения копул, вам нужно понять, какие копулы использовать для определения связей (Гаусса, Стьюдента, Гумбеля или какую ещё). В принципе, тут нет точного научного метода. Кто-то смотрит на парные графики распределения «заархивированных» величин и на глаз определяют копулу. Кто-то использует Хи-графики (тут написано как их использовать). Вопрос мастерства и обширное поле для исследований.
После того как мы решили, какие копулы использовать в парных связях, нам нужно определить их параметры. Это делается численным методом максимального правдоподобия (numerical MLE) по следующим алгоритмам:
Log-likelihood=0;
for i = 1:n
v(0,i) = x(i)
end for
for j = 1:n-1
for i = 1:n-j
Log-likelihood = Log-likelihood + L(v(j-1,1), v(j-1,i+1), param(j,i));
end for
if j == n then
break
end if
for i = 1:n-j
v(j,i) = h(v(j-1,i+1), v(j-1,1), param(j,i));
end for
end for
Log-likelihood=0;
for i = 1:n
v(0,i) = x(i);
end for
for j = 1:n-1
Log-likelihood = Log-likelihood + L(v(0,i),v(0,i+1), param(1,i));
end for
v(1,1) = h(v(0,1),v(0,2), param(1,1))
for k = 1:n-3
v(1,2k) = h(v(0,k+2), v(0,k+1), param(1,k+1));
v(1,2k+1) = h(v(0,k+1), v(0,k+2), param(1,k+1));
end for
v(1,2n-4) = h(v(0,n), v(0,n-1), param(1,n-1));
for j = 2:n-1
for i = 1:n-j
Log-likelihood = Log-likelihood + L(v(j-1,2i-1),v(j-1,2i), param(j,i));
end for
if j == n-1 then
break
end if
v(j,i) = h(v(j-1,1), v(j-1,2), param(j,1));
if n > 4 then
for i = 1:n-j-2
v(j,2i) = h(v(j-1,2i+2),v(j-1,2i+1),param(j,i+1));
v(j,2i+1) = h(v(j-1,2i+1),v(j-1,2i+2),param(j,i+1));
end for
end if
v(j,2n-2j-2) = h(v(j-1,2n-2j),v(j-1,2n-2j-1),param(j,n-j))
end for
Это алгоритмы расчета логарифмической функции правдоподобия, которую, как известно, нужно максимизировать. Это задача для различных оптимизационных пакетов. Тут требуются небольшие пояснения по используемым в «коде» переменным:
х — набор «заархивированных» данных размером T на n, где х ограничены на отрезке (0,1).
v — матрица размером T на n-1 на n-1, куда будут загружаться промежуточные данные.
param — параметры парных копул, которые мы и ищем, максимизируя Log-likelihood.
L(x,v, param) = 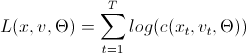
h(x,v, param) = 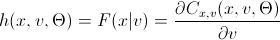
Любители попортить бумагу своими выкладками могут не открывать следующий спойлер, куда я внес h-функции основных копул.
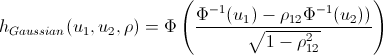
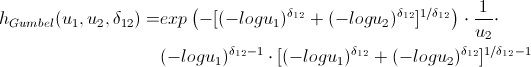
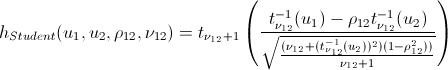
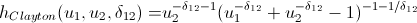
После того как мы нашли параметры наших копул, которые максимизируют логарифмическую функцию правдоподобия, мы можем приступать к генерации случайных величин, которые имеют такую же структуру взаимосвязей, как и наши начальные данные. Для этого тоже существуют алгоритмы:
w = rand(n,1); % Генерируем n равномерно распределенных величин
x(1) = v(1,1) = w(1);
for i = 2:n
v(i,1) = w(i);
for k = i-1:1
v(i,1) = h_inv(v(i,1), v(k,k), param(k,i-k)); % стоит отметить, что здесь идет обратный цикл.
end for
x(i) = v(i,1);
if i = n then
break
end if
for j = 1:i-1
v(i,j+1) = h(v(i,j), v(j,j), param(j,i-j));
end for
end for
w = rand(n,1); % Генерируем n равномерно распределенных величин
x(1) = v(1,1) = w(1);
x(2) = v(2,1) = h_inv(w(2), v(1,1), param(1,1));
v(2,2) = h(v(1,1), v(2,1), param(1,1));
for i = 3:n
v(i,1) = w(i);
for k = i-1:2
v(i,1) = h_inv(v(i,1), v(i-1,2k-2), param(k,i-k));
end for
v(i,1) = h_inv(v(i,1), v(i-1,1), param(k,i-1));
x(i) = v(i,1);
if i == n
break
end if
v(i,2) = h(v(i-1,1), v(i,1), param(1,i-1));
v(i,3) = h(v(i,1), v(i-1,1), param(1,i-1));
if i>3
for j = 2:i-2
v(i,2j) = h(v(i-1,2j-2), v(i,2j-1), param(j,i-j));
v(i,2j+1) = h(v(i,2j-1), v(i-1,2j-2), param(j,i-j));
end for
end if
v(i,2i-2) = h(v(i-1,2i-4), v(i,2i-3), param(i-1,1));
end for
Вы используете параметры, которые получили при помощи алгоритмов оценки модели и генерируете n переменных. Прогоняете данный алгоритм T раз и получаете матрицу T на n, данные в которой имеют такой же паттерн взаимосвязей, как и исходные данные. Единственное нововведение по сравнению с предыдущими алгоритмами — обратная h-функция (h_inv), которая является обратной функцией условного распределения по первой переменной.
Опять-таки, позвольте избавить вас от длительных выкладок:
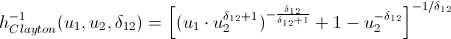
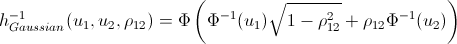
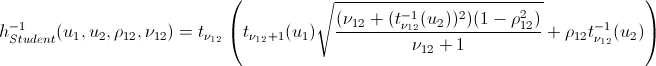
Вот в принципе и все. А теперь обещанный…
Практический пример
1. Для примера я решил поиграть в маленького банковского клерка, которому сказали посчитать дневной VaR по его портфелю. На дворе 1 января 2012 года и у меня в портфеле в равных долях лежат акции 4 компаний: 3M (MMM), Exxon Mobil (XOM), Ford Motors (F) и Toyota Motors(TM). Поприставав к добрым ай-тишникам, добиваясь от них выгрузки с нашего сервера истории цен за последние 6 лет, понял, что им некогда (1 январе на дворе, кто вообще работает???) и выгрузил эту информацию с сервера Яху. Я взял историю цен по дням на периоде с 3 января 2005 по 31 декабря 2011 года. Получилась матрица 1763 на 4.
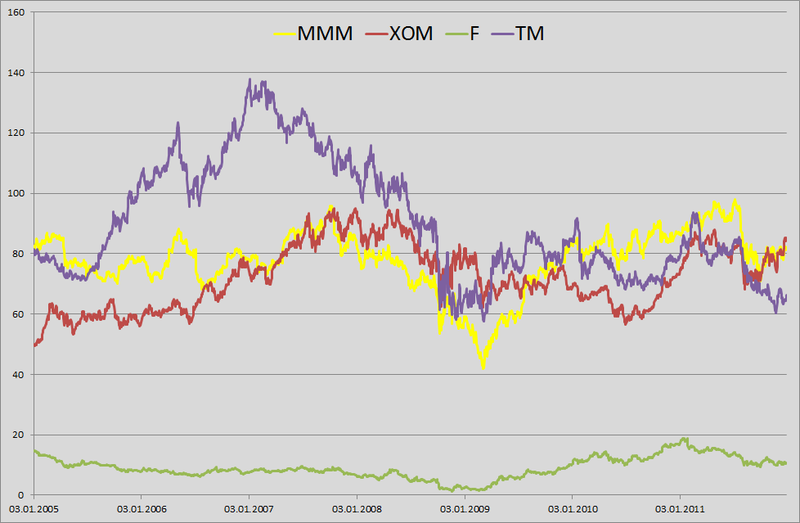
2. Нашёл лог-ретерны: 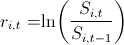 и построил их попарное распределение.
и построил их попарное распределение.
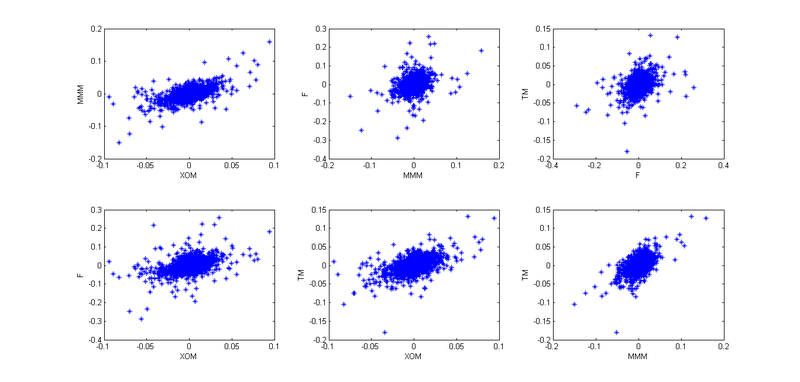
Ну так — чтоб представлять общую картину.
3. Потом я вспомнил лекции по финансам и то, как нам вдалбливали — «ребята, то что ретерны распределены нормально — чушь; в реальной жизни все не так». Подумал, не использовать ли мне тогда предположение, что ретерны распределены по NIG (Normal Inverse Gaussian). Исследования показывают, что это распределение хорошо соответствует эмпирическим данным. Но мне надо придумать модель расчета VaR, а потом пробэктестить ее на исторических данных. Любая модель, не учитывающая кластеризацию второго момента, будет показывать нехорошие результаты. Тогда пришла идея — буду использовать GARCH(1,1). Модель неплохо схватывает 3 и 4 моменты распределения, плюс учитывает волатильность второго момента. Итак я решил, что мои ретерны следуют следующему закону 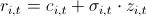 . Тут с — это историческое среднее, z — стандартно нормально распределенная случайная величина, а сигма следует уже своему закону:
. Тут с — это историческое среднее, z — стандартно нормально распределенная случайная величина, а сигма следует уже своему закону: 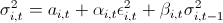 .
.
4. Так, теперь нужно учесть взаимозависимости этих четырех акций. Для начала я использовал эмпирические копулы и построил графики парных зависимостей «заархивированных» наблюдений:
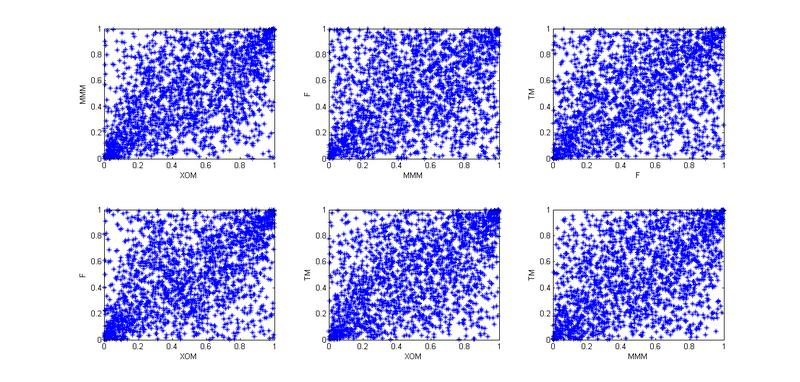
Учитывая, что сегодня 1 января, а я — ленивая скотинка, решил что тут все паттерны похожи на копулу Стьюдента, но чтобы лучше передать взаимозависимости, решил применить не 4-х мерную копулу, а разбить это все на шесть 2-х мерных копул.
5. Для того, чтобы разбить на парные копулы, нужно выбрать порядок представления — каноническая или D-лоза. Для этого я посчитал тау Кендалла, чтобы определить уровень взаимозависимости:
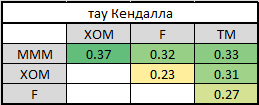
Нетрудно заметить, что самые сильные связи имеет МММ со всеми остальными компаниями. Это предопределяет наш выбор лозы — каноническая. Почему? Нажмите пару раз PageUp и посмотрите на её графическое отображение. В первом дереве все стрелки исходят из одного узла — именно наша ситуация, когда самыми сильными связями обладает одна компания. Если бы высокие тау Кендалла в последней таблице были на разных строчках и разных столбцах, мы бы выбрали D-лозу.
6. Итак мы определили порядок представления и все необходимые попарные копулы — можно приступать к оценке параметров. Применив вышеуказанные алгоритм, я нашёл все необходимые параметры.
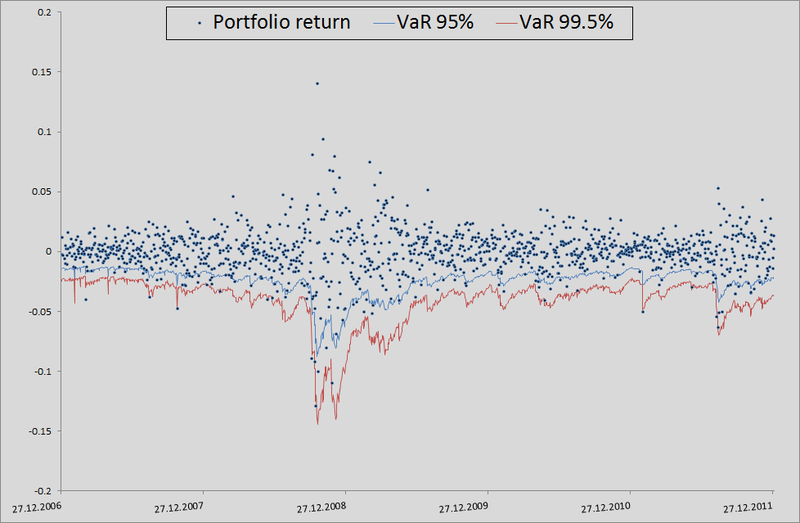
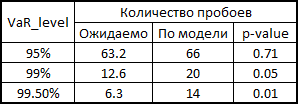
7. Вот тут я немного объясню, как это всё происходило в контексте бэктестинга. Для того, чтобы проверить, насколько моя модель правдоподобно считает VaR, я хотел посмотреть как бы она справлялась в прошлом. Для этого я дал ей небольшую фору — 500 дней и, начиная с 501 дня, я считал мои риск метрики для следующего дня. Имея на руках параметры копул, я генерировал по 10 000 четверок равномерно распределенных величин, получал из них четверки стандартно нормально распределенных величин (шумы) и подставлял в формулу расчета ретерна из 3 пункта данного примера. Туда же я вставлял прогноз сигмы по GARCH(1,1) модели используя данные предыдущих дней (это делалось комбинацией матлабовских функций ugarch и ugarchpred) и исторические средние. Получив таким образом 10 000 четверок ретернов акций, я получал 10 000 ретернов моего портфеля, беря среднее арифметическое от ретернов акций 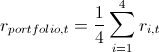 (т.к. у нас равные доли и лог-ретерны, мы имеем право так делать). Потом сортировка и выделение 50-ого, 100-ого и 500-ого значения для 99.5%, 99% и 95% порогового уровня соответственно. Посчитав таким образом риск метрики для оставшихся 1263 дней, я получил красивый график и статистику пробоев уровней.
(т.к. у нас равные доли и лог-ретерны, мы имеем право так делать). Потом сортировка и выделение 50-ого, 100-ого и 500-ого значения для 99.5%, 99% и 95% порогового уровня соответственно. Посчитав таким образом риск метрики для оставшихся 1263 дней, я получил красивый график и статистику пробоев уровней.
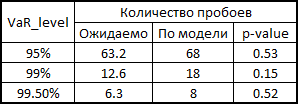
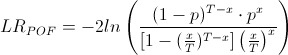
Здесь х — количество пробоев по модели, Т — количество испытаний (у нас = 1263), р — ожидаемая доля пробоев (в нашем случае 0.5%, 1% и 5%).
По нулейвой гипотезе данная статистика имеет хи-квадрат распределение с одной степенью свободы. Найдя статистику, несложно посчитать ее p-value.
В принципе, есть куда еще расти в точности. Но если взять в качестве бенчмарка модель без учета взаимозависимостей вообще, то там вообще швах:
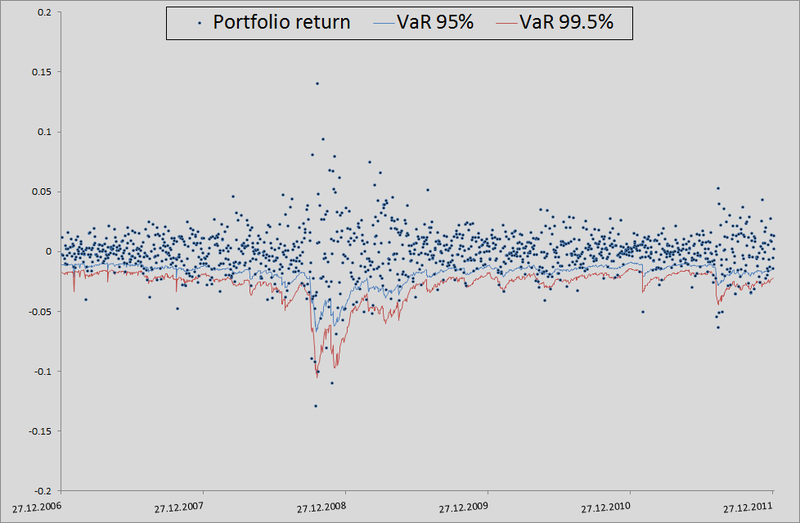
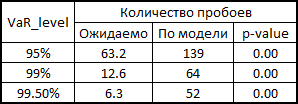
Для честности, нужно показать как бы вела себя модель, если бы мы использовали корреляции и генерировали шумы для расчета ретернов из многомерного нормального распределения:
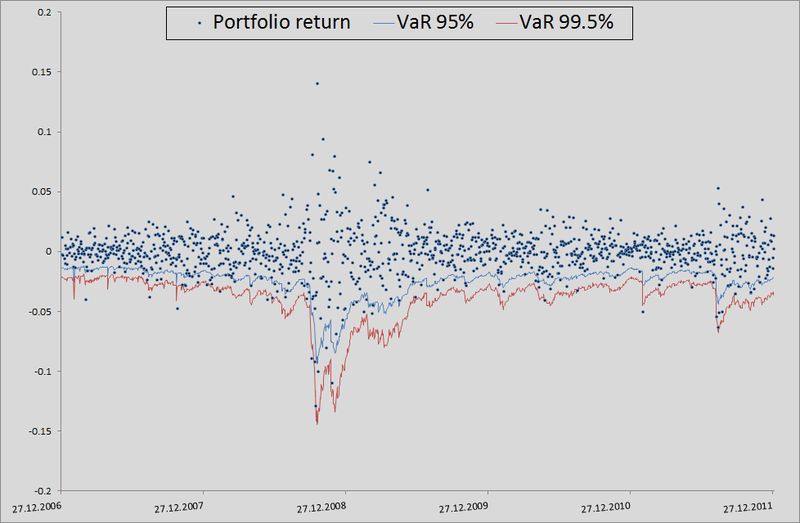
Как видите, для VaR 95% данная модель даже лучше, чем наша. Но чем дальше, тем хуже — как уже упоминалось, нормальное распределение не схватывает хвосты.
В общем, копулы можно использовать, но делать это надо с умом. Они дают более широкие возможности для учета взаимозависимостей, но, как и с любой точной моделью, тут надо быть аккуратным — есть возможность промахнуться в предположениях и получить результаты хуже, чем от стандартной модели.
P.S. Не раз замечал за собой косноязычие, поэтому буду рад, если вы укажете мне на такие моменты в тексте. Я постарался излагать мысли, как можно яснее, но не всегда мне это удается.
Автор: KeKin