Именно о лесенках хотелось бы немного поговорить. Есть такая относительно распространенная задача с программистских собеседований:
Вы поднимаетесь по лестнице. На каждом шаге вы можете подняться либо на 1 ступеньку, либо на 2. Всего лестница имеет n ступенек. Сколькими разными способами вы можете дойти до конце лестницы?
Задача не сильно сложная, но имеющая пару интересных моментов относительно минимально возможной сложности решения и демонстрирующая «штуки, которые интересно знать».
Очевидно, что так или иначе решение начинается с наблюдения, что на каждом шаге у нас есть выбор из двух действий: сделать один шаг или сделать два шага. В первом случае лестница уменьшается на одну ступеньку, во втором — на две. Общее количество возможных способов обойти лестницу равно сумме количества способов сделать это, если мы начинаем с одной ступеньки, и количества способов, если начинаем с двух. В итоге решение сводится к рекуррентной формуле:
F(n) = F(n-1) + F(n-2)
Рекурсивная или итеративная реализация данного алгоритма «в лоб» выглядит ненамного длиннее самого соотношения (проблему переполнения оставляем за скобками):
int f(int n)
{
if (n == 0 || n == 1) return 1;
return f(n-1) + f(n-2);
}
Само по себе это решение верное, но его эффективность низка: алгоритм экспоненциален. Сложность можно уменьшить, воспользовавшись мемоизацией. Интуитивное объяснение: с каждой конкретной ступеньки на лестнице количество способов дойти до конца не зависит от того, как мы попали на эту ступеньку, поэтому ответ имеет смысл запомнить и использовать на следующих шагах расчета. Код приводить не буду — главное, что вкупе с итерацией получается линейное решение. Однако это не все.
Внимательный читатель заметит, что соотношение выше является попросту формулой чисел Фибоначчи с поправкой n на единицу (поправка появляется из-за того, что начальные условия другие — Fib(0) = 0, Fib(1) = 1, Fib(2) = 1, а в нашем случае лесенки F(0) = 1, F(1) = 1, F(2) = 2). Известно, что для чисел Фибоначчи имеет место следующее соотношение:
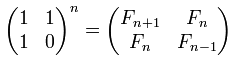
Таким образом, после данного возведения в степень результирующая матрица будет содержать интересующее нас «n+1»-ое число Фибоначчи в первом столбце первой строки (элементы матриц традиционно индексирую с единицы).
Сам по себе этот факт уже интересен, однако особенно интересен он в сочетании с алгоритмом быстрого возведения в степень. Применительно к нашей задаче это означает, что мы можем получить ответ за O(ln N) шагов. Код этого решения на языке Python (опять же, чтобы забыть пока про проблему переполнения — Python автоматически переключается на использование big integer, когда это надо) выглядит так:
#!/usr/bin/env python
# You are climbing a stair case. Each time you can either make 1 step or 2
# steps. The staircase has n steps. In how many distinct ways can you climb the
# staircase?
def mul(a, b):
return ((a[0][0] * b[0][0] + a[0][1] * b[1][0],
a[0][0] * b[0][1] + a[0][1] * b[1][1]),
(a[1][0] * b[0][0] + a[1][1] * b[1][0],
a[1][0] * b[0][1] + a[1][1] * b[1][1]))
def pow(a, N):
"""Fast matrix exponentiation"""
assert N >= 1
if N == 1:
return a
x = pow(a, N / 2)
ret = mul(x, x)
if N % 2:
ret = mul(ret, a)
return ret
def num_stair_ways(N):
x = pow(((1, 1), (1, 0)), N)
return x[0][0]
for i in range(1, 1001):
print i, num_stair_ways(i)
Собственно, все. Надеюсь, как и я, читатель испытывает удовлетворение от осознания факта, что лестницу длиной в 200 ступенек можно прошагать в соответствии с условиями задачи 453973694165307953197296969697410619233826-ю разными способами. И что это может быть подсчитано с логарифмической сложностью.
Автор: aalexand






