Введение
Обычно данный материал приводится с обилием формул и рассчитан больше на математиков. Я постараюсь расписать его наиболее доступно на простых численных примерах с точки зрения применения этого метода в микроэлектронике на аппаратном уровне. В численных примерах для наглядности будет использоваться значение p = 11.
Постановка задачи
Положим, что нам требуется выполнить умножение следующего вида: res = (a*b) mod p, где
0 <= a < p
0 <= b < p
p – простое число.
mod p – операция нахождения остатка по модулю.
И выполнить его надо на низком уровне, где нет как таковой операции умножения и операции взятия остатка от деления или же они реализуются достаточно сложно (например, в электронном устройстве).
Простейшие методы решения
- Первое что приходит в голову: умножить, потом разделить и взять остаток. Этот подход имеет право на существование, но чрезвычайно затратен по количеству операций и довольно сложен для реализации.
- Второе, что можно придумать, это реализовать эту операцию двумерной таблицей умножения размера
pнаp. Что имеет смысл еслиpмало, однако при росте значения p квадратично растут затраты на хранение таблицы (рис. 1).

Рисунок 1. Таблица умножения по модулю p для p = 11.
Умножитель на базе индексного метода
Однако существует метод, который требует одной (или для удобства двух) таблиц размерности p. Метод основан на замене умножения сложением. И может быть схематично проиллюстрирован следующим рисунком (рис. 2):
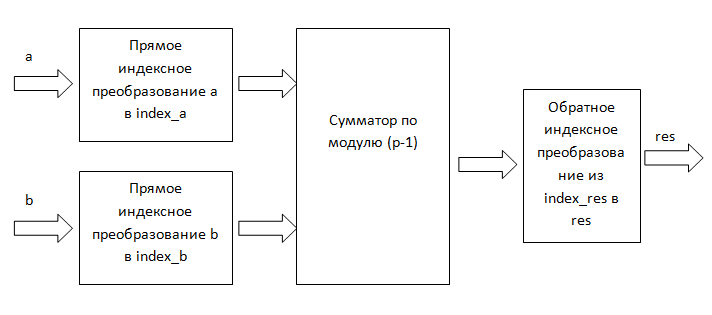
Рисунок 2. Индексное умножение.
Поясним, почему это возможно. Индексное представление числа основывается на понятии первообразного корня по простому модулю p [1]. Первообразным корнем w является целое число, возведение которого в степень 0, 1, 2, …, (p-2) дает неповторяющиеся вычеты по модулю p. Первообразный корень всегда существует для любого простого p (доказано Гауссом в 1801 году). В этом случае каждому целому числу q из промежутка (0; p) можно поставить в соответствие число i такое что: q = (wi) mod p. И таким образом получить следующее соответствие:
(a*b) mod p <-> w^((ia+ib) mod (p-1)) [2].
Рассмотрим пример для модуля p = 11. Первообразный корень w для этого значения модуля равен 2. Как несложно убедиться возведение w в степень 0, 1, … 9 дает неповторяющиеся результаты:
- (20)
mod11 = 1mod11 = 1 - (21)
mod11 = 2mod11 = 2 - (22)
mod11 = 4mod11 = 4 - (23)
mod11 = 8mod11 = 8 - (24)
mod11 = 16mod11 = 5 - (25)
mod11 = 32mod11 = 10 - (26)
mod11 = 64mod11 = 9 - (27)
mod11 = 128mod11 = 7 - (28)
mod11 = 256mod11 = 3 - (29)
mod11 = 512mod11 = 6
Для получения таблицы преобразования между обычным {q} и индексным {i} представлением необходимо отсортировать полученные пары значений в порядке возрастания. Таким образом, таблица прямого преобразования для модуля p = 11 будет выглядеть следующим образом:
| q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| i | 0 | 1 | 8 | 2 | 4 | 9 | 7 | 3 | 6 | 5 |
А таблица обратного преобразования для модуля p = 11 будет выглядеть так:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| q | 1 | 2 | 4 | 8 | 5 | 10 | 9 | 7 | 3 | 6 |
Найдем значение выражения (3*5) mod 11. Числа 3 и 5 имеют соответствующие индексы 8 и 4 (см. таблицу 1). Просуммировав эти индексы по модулю (11-1) = 10 получим результат (8+4) mod 10 = 12 mod 10 = 2. Из таблицы 2 находим, что обратное преобразование для индекса 2 дает конечный результат, равный 4.
Структурную схему индексного умножителя по модулю m=11 для рассмотренного примера можно посмотреть на следующем рисунке (рис 3):
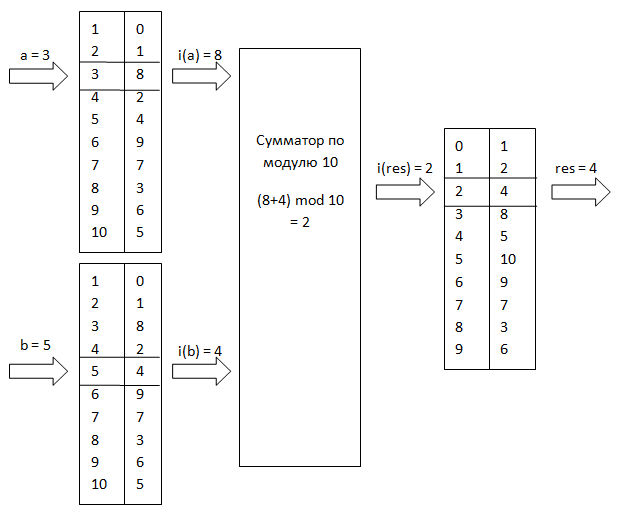
Рисунок 3. Схема индексного умножителя для p = 11.
Нулевые значения для входов
Если внимательно посмотреть на таблицы, то видно, что там не присутствуют нулевые значения для входных данных. Это связано с тем, что wi != 0 ни при каких значениях i. Этот случай обрабатывается отдельно (либо вводится понятие сингулярности со специальными правилами её обработки). Если на одном из входов умножителя появляется 0, то на выходе тоже будет 0, что непосредственно следует из правил умножения.
Распараллеливание умножителя
Оказывается умножение можно сделать ещё быстрее. Если число (p-1) можно разбить на попарно взаимнопростые множители p-1 = m1*m2*…*mr, то операция сложения может быть разбита на r операций сложений меньшей размерности. В этом случае индекс преобразуется в вектор длины r, по следующей формуле: (i mod m1, i mod m2, …, i mod mr). А суммирование производится независимо по каждому элементу вектора.
Рассмотрим это на примере. Для p = 11 значение p-1 = 10 и оно может быть разбито на взаимнопростые множители единственным образом: 10 = 2*5 (m1 = 2, m2 = 5). В этом случае таблица 1 может быть расписана следующим образом:
| q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| i | 0 | 1 | 8 | 2 | 4 | 9 | 7 | 3 | 6 | 5 |
(i mod 2, i mod 5) |
(0, 0) | (1, 1) | (0, 3) | (0, 2) | (0, 4) | (1, 4) | (1, 2) | (1, 3) | (0, 1) | (1, 0) |
А таблица обратного преобразования соответственно так:
(i mod 2, i mod 5) |
(0, 0) | (0, 1) | (0, 2) | (0, 3) | (0, 4) | (1, 0) | (1, 1) | (1, 2) | (1, 3) | (1, 4) |
| q | 1 | 9 | 4 | 3 | 5 | 10 | 2 | 7 | 8 | 6 |
Найдем, как и в прошлом примере, значение (3*5) mod 11. Сначала ищем соответствующие вектора в таблице: 3 -> (0, 3), 5 –> (0, 4). Затем поэлементно складываем ((0 + 0) mod 2, (3 + 4) mod 5) = (0, 2). Из таблицы обратного преобразования находим ответ: (0, 2) -> 4. Схема параллельного умножителя приведена ниже (рис. 4):
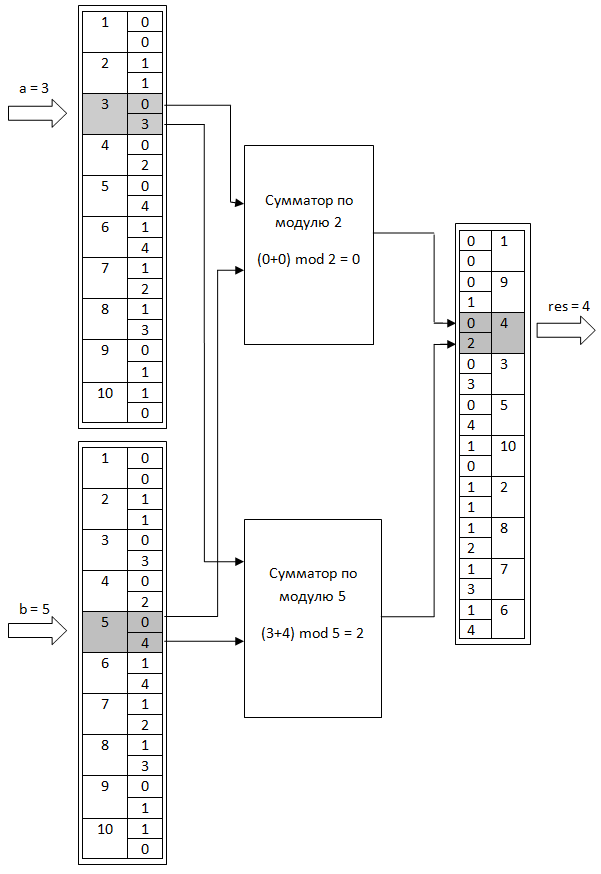
Рисунок 4. Схема параллельного индексного умножителя для p = 11.
Как искать первообразный корень?
Если честно не задавался этим вопросом. Я использую полный перебор, начиная с 2 до p. Либо можно использовать готовую последовательность: oeis.org/A046145. Если есть более эффективный метод пишите в комментах.
Как проектировать сумматор по модулю (p-1)?
Из-за особенностей входных данных сумматора по модулю (p-1), а именно, что на оба входа приходит число меньше, чем p-1, а значит их сумма меньше чем 2*(p-1). Из этого следует, что можно использовать любой из стандартных сумматоров, выход которого корректируется по следующему алгоритму: если значение больше или равно (p-1), то вычесть из результата (p-1), иначе оставить без изменений.
Литература
[1] ru.wikipedia.org/wiki/%D0%9F%D0%B5%D1%80%D0%B2%D0%BE%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BD%D1%8B%D0%B9_%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D1%8C_%28%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D1%87%D0%B8%D1%81%D0%B5%D0%BB%29
[2] www.researchgate.net/publication/224735018_A_fast_RNS_Galois_field_multiplier
От автора
Если у вас есть дополнения по статье буду рад их увидеть в комментариях. И ещё статья получилась бедной на ссылочки с подробностями, если у кого что есть кидайте. =)
Автор: Turbo





