В последнее время приходится все больше задумываться о сохранности анонимности и безопасности относительно прав на информационную собственность. В этой заметке я предложу довольно интересное решение относительно шифрования, позволяющего сохранить несколько различных объектов в одном контейнере с разными мастер-ключами, и гарантирующее отсутствие «следов» других сущностей при получении какой-либо одной. Более того, в силу конструктивных особенностей алгоритма — даже наличие расшифрованной сущности можно всегда списать на «случайность» (то есть, нет никаких средств проверить, были ли изначально зашифрованы эти данные или нет). Кроме того, алгоритм имеет чрезвычайную стойкость к атакам «подбора ключа». Правда у метода есть и существенный недостаток — катастрофически низкая скорость работы, но в ряде особенных случаев он все равно может быть полезен.
Ядро метода — математический объект под названием хеш-функция. В качестве небольшого ликбеза рекомендую изучить также и мою предыдущую заметку.
Существует ряд довольно занятных заблуждений о хеш-функциях:
- Хеш-функцию легко обратить. Якобы существует некая программа md5decrypt, которая восстанавливает результат md5crypt;
- Хеш-функции вроде MD5 уже давно сломаны, т.к. получить коллизию на заданную строку — плевое дело;
- Хеш-функции являются алгоритмом шифрования.
Все это — очевидно ерунда. Криптографические хеш-функции по определению сложны для обращения, и для используемых ныне методов (MD5, SHA) никто обратного не доказал. Коллизии мы научились строить только в самом общем виде, генерируя разные строки s1, s2, такие что f(s1) = f(s2). А шифрованием хеширование не является, хотя бы потому, что отсутствует понятие ключей шифрования.
Но иногда «ерунда» может помочь сконструировать интересное решение, попробуем на секунду представить, что вышеизложенные тезисы справедливы. Даже не так, построим объект, для которого они будут выполняться.
Пусть R(key, message) = первые N бит md5(key + message), где N — не очень велико, скажем равно 40. И тут начинается интересное!
Во-первых, при заданном ключе key, мы без труда можем строить большое количество разных сообщений, дающих нужное значение функции. Перебрать порядка 2^40 различных строк — задача посильная обычному «домашнему» компьютеру. Если мы имеем заданное значение X, которое является результатом применения функции R мы без труда найдем и прообраз.
То есть, пусть X = R('test_key', 'msg') = 5B7AF38712
Забываем про сообщение 'msg', имеем только хеш-значение 5B7AF38712 и исходный ключ 'test_key', запускаем перебор, и через некоторое время получаем строку 'msg' в качестве прообраза!
Но что, если мы не знаем и ключа ('test_key') а знаем только хеш-значение? Тогда мы можем построить бесконечное количество пар ключ-сообщение, дающие наше значение X.
Некоторые из этих пар даже будут выглядеть осмысленно, что бы это ни значило. Более того, одной из таких пар будет главный вопрос жизни вселенной и всего такого (в некоторой формулировке) и ответ на него.
Почему так? Просто потому, что множество входных значений (то есть ключей и сообщений) бесконечно, а функция R обладает конечным количеством возможных значений, каждое из которых (очень грубо говоря) имеет равные шансы на появление.
Теперь, думаю, идея процесса понятна — отправляя человеку '5B7AF38712', он, зная ключ ('test_key'), быстрее всего получит сообщение ('msg') (но пока нет гарантий этого, нужно заметить). А, не зная, — любой мусор.
Магия
Теперь мы хотим научиться кодировать сообщения так, чтобы адресат смог расшифровать их правильно с определенными гарантиями. А еще, мы довольно хитры, и хотим чтобы та же посылка могла быть расшифрована с другим ключом как другое заданное сообщение.
То есть, на входе: key1, message1 и key2, message2.
Причем crypt(key1,message1,key2,message2) = X,
и decrypt(X,key1) = message1, а decrypt(X,key2) = message2.
Здесь нам придется «модернизировать» функцию R, мы построим целый набор функций:
Rm(key,msg) = первые N бит md5(key + строка(m) + msg),
где строка(m) — любое однозначное представление числа m как строки (например десятичная запись).
Индекс m — специальное «контрольное значение», которое мы будем варьировать при шифровании сообщений (то есть, оно выбирается нашим алгоритмом).
Прежде чем рассказать, как оно выбирается, я предложу процедуру расшифровки, благо она довольно проста:
decrypt(X,key) = значение msg, такое, что R(key,msg) == X, при наименьшем m.
В итеративной форме можно записать так (псевдокод):
string decrypt(X, key)
{
for (int m = 0; m < MAX_INT; m++)
for (string msg in generate_all_strings(MAX_STRING_LEN) )
if (first_N_bytes( md5( key + m.ToString() + msg) ) == X) // R()
return msg;
}
Коллизию для первых 40 бит получить несложно, и эта функция гарантированно вернет какое-либо значение. Задача функции «шифрования» обеспечить возврат нужного значения.
Но ведь это тоже можно сделать перебором:
string encrypt(key, msg)
{
for (int m = 0; m < MAX_INT; m++)
{
string X = first_N_bytes( md5( key + m.ToString() + msg) ); // R()
if (decrypt(X, key) == msg)
return X;
}
}
Таким образом, мы обеспечиваем уверенность в верной расшифровке ее моделированием с различными параметрами. Если алгоритм расшифровки не меняется, то это гарантия корректности, и заметьте — никаких контрольных сумм, валидаторов, прочих вещей, позволяющих «выдать» факт правильной расшифровки!
Изначально я говорил про возможность шифрования сразу двух сообщений, что по сути сейчас становится самоочевидным фактом:
string encrypt(key, msg, key2, msg2)
{
for (int m = 0; m < MAX_INT; m++)
{
string X = first_N_bytes( md5( key + m.ToString() + msg) ); // R()
if (decrypt(X, key) == msg && decrypt(X, key2) == msg2)
return X;
}
}
Однако здесь есть есть некоторые подводные камни — при фиксированном диапазоне «контрольных значений» (m) — такой функции Rm может не существовать, и придется расширять диапазон. А расширение диапазона снижает скорость алгоритма. В общем случае диапазон для значения m должен быть больше, чем разрядность хеш-функции R, так что мы можем просто ее уменьшить (что я и сделал в тестовом прототипе). Но при сильно уменьшенном диапазоне выходных значений таких m тоже может просто не существовать.
В целом при реализации прототипа я остановился на двухбайтном усечении. Кроме того, для частичного решения вопроса производительности (я быстро набросал прототип на C#, а «местные» провайдеры криптографии просто ужасно медлительны! Практически в 50000 раз медленнее, чем реализация на GPU, которую я постараюсь выполнить чуть позже) я оставил возможность использовать только буквы диапазона a-z. В таком «печальном» виде это уже работает. Вводим две пары ключ-значение, жмем «Encrypt2» и получаем через некоторое время хеш-код. С первым ключом он быстро расшифровывается в первое сообщение:
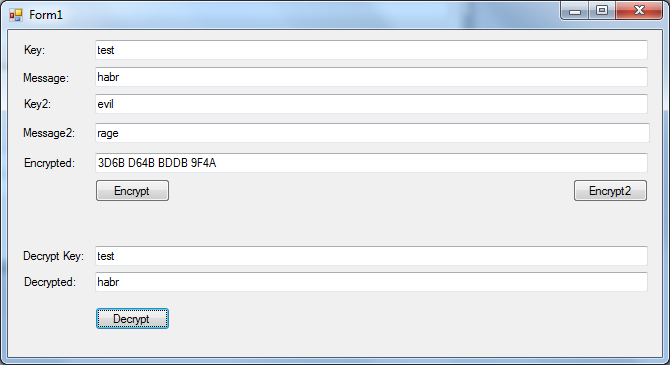
Со вторым, соответственно, во второе:
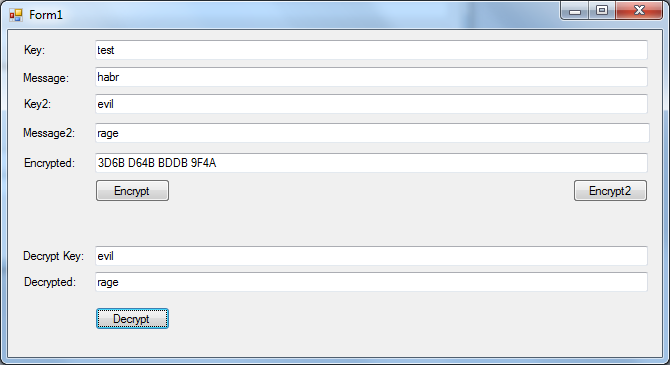
Заметьте, все тот же encrypted text. Ну а с неправильным ключом — в странное сообщение (но где гарантии, что не оно было исходным?):
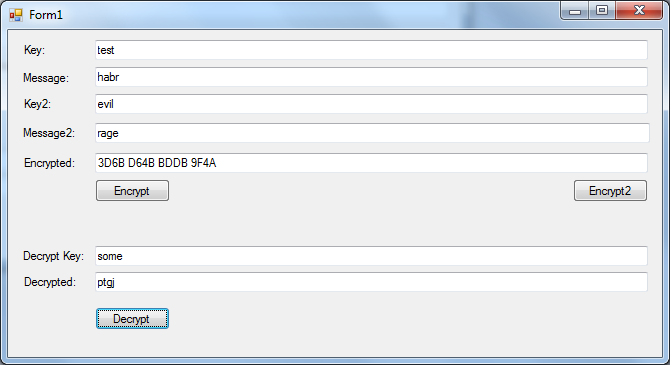
Скачать прототип можно отсюда: dl.dropbox.com/u/243445/md5h/HashCode.7z
В нем довольно много нелепых ограничений, но для возмущенных, напомню, что это просто иллюстрация идеи. А над хорошим приложением при условии актуальности идеи можно будет и подумать.
Автор: sic
