Этот пост я хочу посвятить приятному трофею, добытому в англоязычном интернете. Речь пойдет об одном из методов адаптивной бинаризации изображений, методе Брэдли (или Брэдли-Рота, поскольку авторов двое).
Немного теории
Процесс бинаризации – это перевод цветного (или в градациях серого) изображения в двухцветное черно-белое. Главным параметром такого преобразования является порог t – значение, с которым сравнивается яркость каждого пикселя. По результатам сравнения, пикселю присваивается значение 0 или 1. Существуют различные методы бинаризации, которые можно условно разделить на две группы – глобальные и локальные. В первом случае величина порога остается неизменной в течение всего процесса бинаризации. Во втором изображение разбивается на области, в каждой из которых вычисляется локальный порог.
Главная цель бинаризации, это радикальное уменьшение количества информации, с которой приходится работать. Просто говоря, удачная бинаризация сильно упрощает последующую работу с изображением. С другой стороны, неудачи в процессе бинаризации могут привети к искажениям, таким, как разрывы в линиях, потеря значащих деталей, нарушение целостности объектов, появление шума и непредсказуемое искажение символов из-за неоднородностей фона. Различные методы бинаризации имеют свои слабые места: так, например, метод Оцу может приводить к утрате мелких деталей и „слипанию“ близлежащих символов, а метод Ниблэка грешит появлением ложных объектов в случае неоднородностей фона с низкой контрастностью. Отсюда следует, что каждый метод должен быть применен в своей области.
Объект тестирования
На данный момент я занимаюсь распознаванием показаний бытовых приборов в рамках популярной идеи „умного дома“. Вот пример изображения, с которыми работает наша группа:

Фотография была сделана темной-темной ночью в темной-темной комнате; светодиодная подсветка сбоку создает сильно неоднородный фон, а между камерой и табло прибора находится силикатное стекло, которое порождает дополнительный шум и ложные образования в области фона. Наша задача – подготовка изображения к распознаванию текста.
Здесь логично использовать локальные методы, они же адаптивные. Наиболее быстрым из классических локальных алгоритмов считается метод Ниблэка, но он плохо работает с низкоконтрастными неровностями фона, которые в нашем случае заполняют изображение чуть меньше, чем полностью. Чтобы исправить этот недостаток, умные люди разработали несколько модификаций метода Ниблэка, называемых „ниблэковскими“. В моем случае один из них, метод Кристиана, показывал хорошие результаты на большинстве образцов, и чуть не был принят в качестве рабочего варианта. Однако на других образцах после применения этого алгоритма появлялись искажения.

а) метод Ниблэка б) метод Кристиана
Суть метода Брэдли
Само по себе сравнение двух величин – порога и яркости пикселя, — является элементарной задачей. Не в этом соль. Трудность заключается в нахождении порогового значения, которое должно максимально надежно отделять символы не только от фона, но и от шума, теней, бликов и прочего информационного мусора. Часто для этого прибегают к методам математической статистики. В методе Брэдли мы заходим с другой стороны – со стороны интегральных изображений.
Интегральные изображения
Интегральные изображения – это не только эффективный и быстрый (всего за один проход по изображению) способ найти сумму значений пикселей, но и простой способ найти среднее значение яркости в пределах заданного участка изображения.
Как это работает? Да элементарно. Допустим, у нас есть 8-битное изображение в оттенках серого (цветное изображение можно перевести в оттенки серого, пользуясь формулой I = 0.2125R + 0.7154G + 0.0721B). В таком случае, значение элемента интегрального изображения рассчитывается по формуле:
S(x, y) = I(x, y) + S(x-1, y) + S(x, y-1) – S(x-1, y-1);
где S – результат предыдущих итераций для данной позиции пикселя, I – яркость пикселя исходного изображения. Если координаты выходят за пределы изображения, они считаются нулевыми. Сущность этого метода „на пальцах“ представлена на схеме ниже:
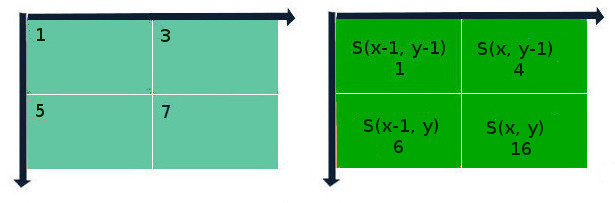
Лайфхак состоит в том, что, один раз составив интегральную матрицу изображения, можно быстро вычислять сумму значений пикселей любой прямоугольной области в пределах этого изображения. Пусть ABCD – интересующая нас прямоугольная область.
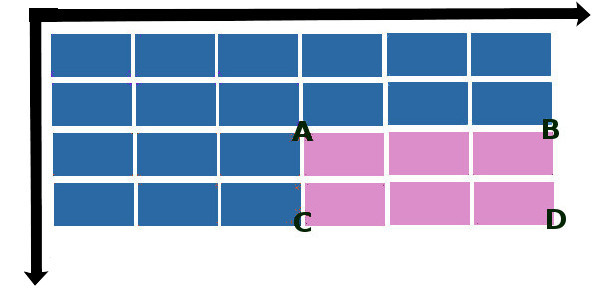
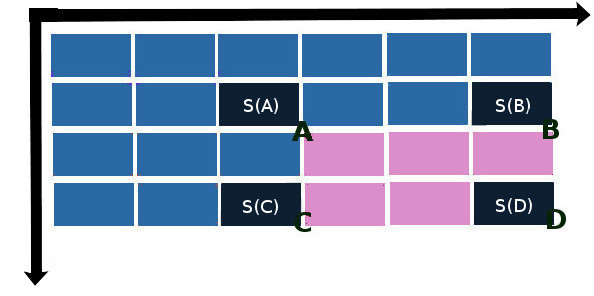
Тогда суммарная яркость S в этой области вычисляется по формуле:
S(x, y) = S(A) + S(D) – S(B) – S©
где S(A), S(B), S© и S(D) – значения элементов интегральной матрицы в направлении на „северо-запад“ от пересечений сторон прямоугольника:
Реализация
Если вы дочитали до этого места, то вы почти разобрались в алгоритме Брэдли. Дальше все просто. Разбиваем изображение на несколько областей со стороной d, берем среднее от суммы значений пикселей Im в этой области, добавляем некоторую величину t, сравниваем значение каждого пикселя с получившимся результатом. Im+t – и есть наша искомая пороговая величина. Брэдли и Рот берут значения d и t соответственно 1/8 от ширины изображения и 15% от среднего значения яркости пикселей по области. Ну а вообще говоря, оба этих параметра могут и должны изменяться в соответствии с конкретной ситуацией. Так, если размеры объекта будут больше площади квадрата со стороной, равной d, то центр этого объекта может быть принят алгоритмом как фон, и проблема решается уменьшением значения d, однако при этом могут быть потеряны мелкие детали изображения.
Реализация алгоритма Брэдли-Рота на С++ представлена ниже:
void Bradley_threshold(unsigned char* src, unsigned char* res, int width, int height) {
const int S = width/8;
int s2 = S/2;
const float t = 0.15;
unsigned long* integral_image = 0;
long sum=0;
int count=0;
int index;
int x1, y1, x2, y2;
//рассчитываем интегральное изображение
integral_image = new unsigned long [width*height*sizeof(unsigned long*)];
for (int i = 0; i < width; i++) {
sum = 0;
for (int j = 0; j < height; j++) {
index = j * width + i;
sum += src[index];
if (i==0)
integral_image[index] = sum;
else
integral_image[index] = integral_image[index-1] + sum;
}
}
//находим границы для локальные областей
for (int i = 0; i < width; i++) {
for (int j = 0; j < height; j++) {
index = j * width + i;
x1=i-s2;
x2=i+s2;
y1=j-s2;
y2=j+s2;
if (x1 < 0)
x1 = 0;
if (x2 >= width)
x2 = width-1;
if (y1 < 0)
y1 = 0;
if (y2 >= height)
y2 = height-1;
count = (x2-x1)*(y2-y1);
sum = integral_image[y2*width+x2] - integral_image[y1*width+x2] -
integral_image[y2*width+x1] + integral_image[y1*width+x1];
if ((long)(src[index]*count) < (long)(sum*(1.0-t)))
res[index] = 0;
else
res[index] = 255;
}
}
delete[] integral_image;
}
Достоинства и недостатки
Достоинствами метода Брэдли-Рота являются простота реализации и высокая скорость выполнения; для большинства случаев нет нужды подбирать параметры. Метод хорошо работает с неоднородным фоном.
Из последнего достоинства логически вытекает недостаток метода Брэдли, а именно, плохая чувствительность к низкоконтрастным деталям изображения:
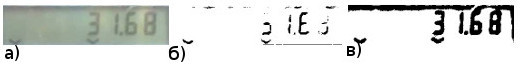
а) оригинальное изображение б) метод Брэдли в) метод Кристиана
Ссылки:
http://citeseerx.ist.psu.edu — оригинальная статья Брэдли и Рота (на английском)
https://computersciencesource.wordpress.com — автор предельно ясно описывает суть интегральных изображений (на английском)
Автор: Llammt







А может сначала шарпинг ?