В первой части статьи мы рассмотрели универсальный автомат Левенштейна — мощный инструмент для фильтрации слов, отстоящих от некоторого слова W на расстояние Левенштейна не более заданного. Теперь пришло время изучить способы применения этого инструмента для эффективного решения задачи нечеткого поиска в словаре.
Самый простой и самый очевидный алгоритм решения задачи нечеткого поиска в словаре с использованием автомата Левенштейна — алгоритм полного перебора. В этом случае для каждого слова в словаре выполняется оценка расстояния Левенштейна (Дамерау-Левенштейна) до поискового запроса. Пример реализации на С# можно посмотреть в первой части статьи.
Применение даже этого простого алгоритма дает выигрыш в производительности по сравнению с применением методов динамического программирования. Однако, существуют более эффективные алгоритмы.
Базовый алгоритм Шульца и Михова
Рассмотрим первый такой алгоритм — насколько мне известно, он был предложен Шульцом и Миховым (2002), поэтому я буду называть его базовым алгоритмом Шульца и Михова или просто базовым алгоритмом. Итак, пусть для предположительно искаженного слова W и порогового значения расстояния редактирования N задан детерминированный автомат Левенштейна AN(W). Пусть рассматриваемый словарь D также представлен в виде детерминированного конечного автомата AD, имеющего входной алфавит E. Состояния автоматов будем обозначать как q и qD соответственно, функции переходов как V и VD, а множество конечных состояний как F и FD. Предложенный Шульцом и Миховым алгоритм нечеткого поиска в словаре представляет собой стандартную процедуру поиска с возвратом и может быть описан следующим псевдокодом:
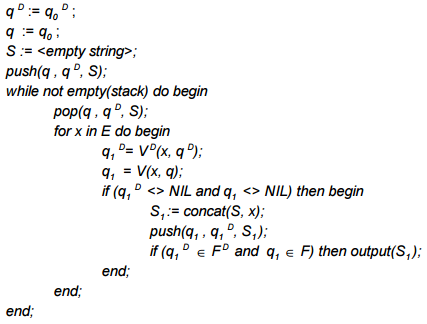
Алгоритм начинает работу с начальными состояниями автоматов. По мере подачи на вход новых символов, в стек помещаются последующие состояния если они не пусты. Если очередные состояния обоих автоматов являются конечными — обнаружено искомое слово.
Этот алгоритм можно еще представить себе как «пересечение» конечных автоматов. В результирующую выборку попадают только те слова, которые соответствуют конечным состояниям обоих автоматов. При этом рассматриваются только те префиксы, которые переводят оба автомата в непустое состояние.
Вычислительная сложность алгоритма зависит от размера словаря и расстояния редактирования N. Если N достигает размера самого длинного слова в словаре, то алгоритм сводится к полному перебору состояний автомата AD. Но при решении практических задач, как правило, используются малые значения N. В этом случае алгоритм рассматривает лишь очень небольшое подмножество состояний автомата AD. При N=0 алгоритм находит в словаре слово W за время O(|W|).
Стоит отметить, что описанный алгоритм обеспечивает отсутствие потерь при поиске. То есть 100% слов в словаре, отстоящих от W на расстояние не более N попадут в результирующую выборку.
Особенности программной реализации
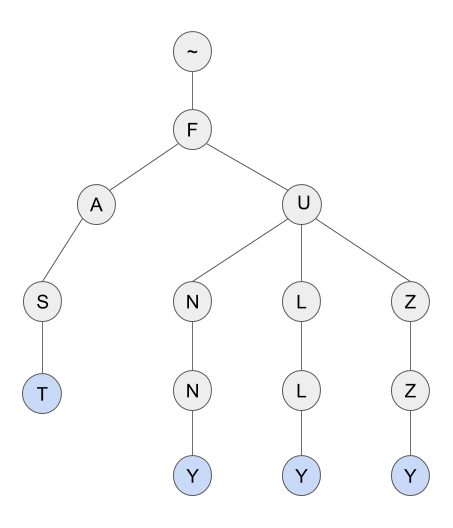
Полагаю, вы уже знакомы с такой структурой данных как префиксное дерево. Префиксное дерево известно также как “нагруженное дерево” (или “бор”, “луч”, “Trie”) и успешно используется для хранения словарей. На рисунке представлено префиксное дерево для словаря из четырех слов: “fast”, “funny”, “fully”, “fuzzy”.
Если вы не знакомы с префиксным деревом, то можете ознакомиться с публикациями, в которых эта структура рассмотрена подробно, например, здесь.
Почему я хочу использовать для хранения словаря префиксное дерево? Потому что префиксное дерево может быть рассмотрено как конечный автомат. Каждый узел дерева представляет собой состояние автомата. Начальным состоянием является корень дерева, а конечными состояниями — узлы, соответствующие словам. Для каждого узла и символа возможен только один переход — автомат является детерминированным.
Итак, рассматривая префиксное дерево как детерминированный конечный автомат и имея программную реализацию детерминированного автомата Левенштейна, нетрудно превратить псевдокод алгоритма в код на каком-либо языке программирования. Под спойлером пример на C#.
/// <summary>
/// Find all words in dictionary such that Levenstein distance to typo less or equal to editDistance
/// </summary>
/// <returns>Set of possible corrections</returns>
/// <param name="typo">Garbled word.</param>
/// <param name="dictionary">Dictionary.</param>
/// <param name="editDistance">Edit distance.</param>
IEnumerable<string> GetCorrections(string typo, TrieNode dictionary, int editDistance) {
var corrections = new List<string> ();
if (string.IsNullOrEmpty (typo.Trim())) {
return corrections;
}
//Create automaton
LevTAutomataImitation automaton = new LevTAutomataImitation (typo, editDistance);
//Init stack with start states
Stack<TypoCorrectorState> stack = new Stack<TypoCorrectorState> ();
stack.Push (new TypoCorrectorState () {
Node = dictionary,
AutomataState = 0,
AutomataOffset = 0,
});
//Traversing trie with standart backtracking procedure
while (stack.Count > 0) {
//State to process
TypoCorrectorState state = stack.Pop();
automaton.LoadState (state.AutomataState, state.AutomataOffset);
//Iterate over TrieNode children
foreach (char c in state.Node.children.Keys) {
//Evaluate state of Levenstein automaton for given letter
int vector = automaton.GetCharacteristicVector (c, state.AutomataOffset);
AutomataState nextState = automaton.GetNextState (vector);
//If next state is not empty state
if (nextState != null) {
TrieNode nextNode = state.Node.children [c];
//Push node and automaton state to the stack
stack.Push (new TypoCorrectorState () {
Node = nextNode,
AutomataState = nextState.State,
AutomataOffset = nextState.Offset
});
//Check if word with Levenstein distance <= n found
if (nextNode.IsWord && automaton.IsAcceptState (nextState.State, nextState.Offset)) {
corrections.Add (nextNode.Value);
}
}
}
}
return corrections;
}
Алгоритм FB-Trie
Идем дальше. В 2004 году Михов и Шульц предложили модификацию вышеописанного алгоритма, основная идея которой заключается в использовании прямого и обратного префиксного дерева в сочетании с разбиением поискового запроса W на две примерно равные части W1 и W2. Алгоритм известен под названием FB-Trie (от forward и backward trie).
Под обратным префиксным деревом следует понимать префиксное дерево, построенное по инверсиям всех слов словаря. Инверсией слова я называю просто слово записанное задом наперед.
Важный момент — в своей работе Михов и Шульц показали, что расстояние Дамерау-Левенштейна между инверсиями двух строк равно расстоянию между самими строками.
Работа алгоритма для N=1 основана на следующем утверждении: любую строку S, которая отстоит от строки W на расстояние Дамерау-Левенштейна d(S, W) <= 1, возможно разделить на две части S1 и S2 только так, чтобы выполнялось одно из трех взаимоисключающих условий:
а) d(S1, W1) = 0 и d(S2, W2) <= 1

б) d(S1, W1) <= 1 и d(S2, W2) = 0

в) d(S1, W1’) = 0 и d(S2, W2’) = 0
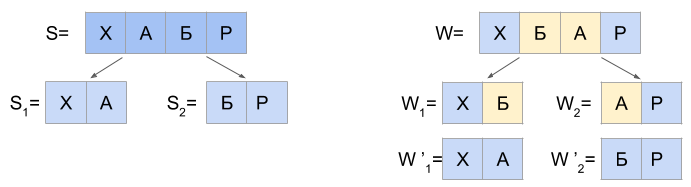
В пункте “в” строки W1’ и W2’ получаются из строк W1 и W2 путем замены последнего символа W1 на первый символ W2 и наоборот. Например, если W1=’FU’, а W2=’ZZY’, то W1’=’FZ’, а W2’=’UZY’.
Как можно быстро найти в словаре все слова, которые подходят под вариант “а”? Очень просто: найти в префиксном дереве узел с префиксом W1, затем обойти всех его наследников в соответствии с базовым алгоритмом Шульца и Михова и отобрать те, ключи которых отстоят от W2 на расстояние не более 1.
//May be for some S d(S1, W1) = 0 and d(S2, W2) <= 1?
TrieNode lnode = ForwardDictionary.GetNode (left);
if (lnode != null) {
corrections.AddRange(GetCorrections(right, lnode, 1));
}
Для варианта “б” пригодится обратное префиксное дерево: найдем в нем узел, соответствующий инвертированной строке W2, затем обойдем всех его наследников и отберем те, ключи которых отстоят от инвертированного W1 на расстояние не более 1 — опять же в соответствии с базовым алгоритмом.
//May be for some S d(S1, W1) = 1 and d(S2, W2) = 0?
TrieNode rnode = BackwardDictionary.GetNode (rright);
if (rnode != null) {
corrections.AddRange(GetCorrections(rleft, rnode, 1))));
}
Для варианта “в” необходимо просто поменять местами два символа в слове W на границе разбиения и проверить содержится ли в префиксном дереве полученное слово.
//May be there is a transposition in the middle?
char[] temp = typo.ToCharArray ();
char c = temp [llen - 1];
temp [llen - 1] = temp [llen];
temp [llen] = c;
TrieNode n = ForwardDictionary.GetWord (new string(temp));
if (n != null) {
corrections.Add (n.Key);
}
Чтобы решить задачу нечеткого поиска в словаре алгоритмом FB-Trie, необходимо просто найти три вышеперечисленных множества слов и объединить их.
Для N=2 потребуется рассмотреть на два случая больше:
а) d(S1, W1) = 0 и d(S2, W2) <= 2

б) 1 <= d(S1, W1) <= 2 и d(S2, W2) = 0
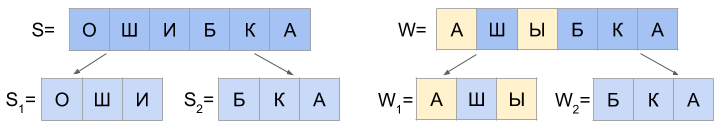
в) d(S1, W1) = 1 и d(S2, W2) = 1
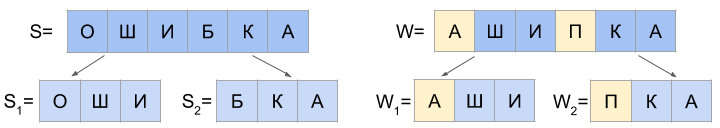
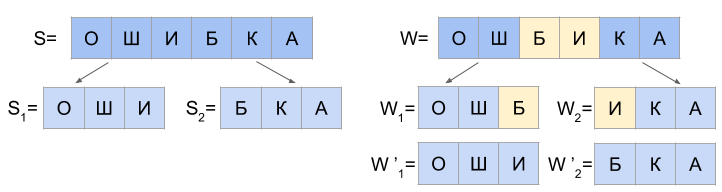
И если последний символ строки S1 равен первому символу W2, а последний символ W1 равен первому символу S2, то возможны еще два случая:
г) d(S1, W1’) = 0 и d(S2, W2’) <= 1
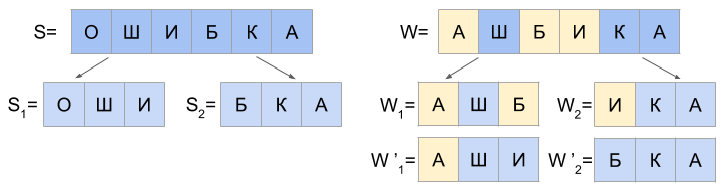
д) d(S1, W1’) <= 1 и d(S2, W2’) = 0
Первые два случая легко обнаруживаются по аналогии с вариантами “а” и “б” для N=1, но используется автомат Левенштейна для N=2.
Варианты “г” и “д” для N=2 повторяют варианты “а” и “б” для N=1, только вместо подстрок W1 и W2 используются W1’ и W1’.
Вариант “в” чуть-чуть сложнее. На первом шаге необходимо найти в прямом префиксном дереве все узлы, соответствующие префиксам, которые отстоят от W1 на расстояние не более 1 (базовый алгоритм). На втором шаге для каждого такого узла необходимо выполнить обход дочерних и отобрать те, которые соответствуют ключам, отстоящим от W2 на расстояние не более 1 (опять же базовый алгоритм).
Для N=3 потребуется рассмотреть уже семь случаев. Приводить их здесь не буду — можете посмотреть в оригинальной статье Михова и Шульца (2004). По аналогии можно продолжить для произвольного N, хотя необходимость в этом при решении практических задач вряд ли возникнет.
Оценки производительности
Любопытно, что время поиска с использованием алгоритма FB-Trie уменьшается по мере увеличения длины слова W.
Детальный анализ времени поиска с помощью алгоритма FB-Trie в сравнении с другими широко известными алгоритмами нечеткого поиска можно найти в работе Леонида Бойцова “Indexing Methods for Approximate Dictionary Searching: Comparative Analysis” (2011). В работе проведено обстоятельное сравнение времени поиска и объема потребляемой памяти для таких алгоритмов как:
- полный перебор;
- различные модификации метода n-грамм;
- различные модификации метода расширения выборки;
- хэширование по сигнатуре;
- FB-Trie и другие алгоритмы.
Я не буду повторять здесь все многочисленные цифры и графики, а ограничусь лишь общими выводами для естественных языков.
Итак, алгоритм FB-Trie обеспечивает разумный компромисс между производительностью и потреблением памяти. Если в вашей прикладной задаче необходимо поддерживать расстояние редактирования 2 и более, а словарь содержит более 500,000 слов — алгоритм FB-Trie рациональный выбор. Он обеспечит минимальное время поиска при разумном расходе памяти (порядка 300% от объема памяти, занимаемого лексиконом).
Если вы решили ограничиться расстоянием редактирования N=1, или у вас маленький словарь, то ряд алгоритмов может работать быстрее (например, Mor−Fraenkel method или FastSS), однако, будьте готовы к повышенному расходу памяти (до 20,000% от размера лексикона). Если вы располагаете десятками гигабайт ОЗУ для хранения нечеткого индекса, вы можете использовать эти методы и при больших размерах словаря.
Чтобы читатель мог решить насколько это много — 500,000 слов, приведу некоторые цифры по количеству слов русского языка (взято отсюда).
- Орфографический словарь Лопатина содержит 162,240 слов — размер файла лексикона 2 МБ.
- Перечень российских фамилий включает не менее 247,780 фамилий — размер файла лексикона 4,6 МБ.
- Полная акцентуированная парадигма русского языка по А. А. Зализняку — это 2,645,347 словоформ, размер файла лексикона около 35МБ.
А что если вы не имеете возможности хранить словарь в виде двух префиксных деревьев? Например, он представлен в виде сортированного списка. В этом случае использование автомата Левенштейна для нечеткого поиска возможно, но нецелесообразно. Возможно — потому что остаются различные модификации полного перебора (например, с отсечением по длине слова |W| плюс минус N). Нецелесообразно — потому что вы не получите выигрыша в производительности по сравнению с более простыми в реализации методами (например, алгоритмом расширения выборки).
Отмечу, что базовый алгоритм Шульца и Михова требует в два раза меньше памяти, чем алгоритм FB-Trie. Однако, за это придется заплатить увеличением времени поиска на порядок (оценка авторов алгоритма).
На этом рассмотрение алгоритмов нечеткого поиска в словаре с использованием автомата Левенштейна считаю законченным.
Да, полные исходные тексты Spellchecker-а на C# можно найти здесь. Наверное, моя реализация не оптимальна с точки зрения производительности, но поможет вам понять работу алгоритма FB-Trie и, возможно, пригодится при решении ваших прикладных задач.
Всем прочитавшим публикацию — огромное спасибо за проявленный интерес.
Ссылки
- Первая часть моей публикации
- Автомат Левенштейна и базовый алгоритм Шульца и Михова (2002)
- Поиск с возвратом
- Алгоритм FB-Trie в статье Михова и Шульца (2004)
- Сайт Леонида Бойцова, посвященный нечеткому поиску
- Хороший пост о нечетком поиске в словаре и тексте
- Пост на Хабре о префиксном дереве
- Алгоритм FastSS
- Исходные тексты к статье на С#
- Реализации на java: раз и два
- Набор словарей русского языка
Автор: IBendrup






