В данной работе даются элементы введения в классификацию с обучением на малых выборках — от удобной системы обозначений до специальных оценок надежности. Постоянное наращивание быстродействия вычислительных устройств и малые выборки, позволяют пренебречь значительным объемом вычислений, необходимым при получении некоторых из этих оценок.
Определения и обозначения
Пусть задано некоторое исходное разбиение множества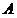 
объектов 
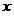на два подмножества (класса) 
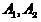, таких, что
, 
.
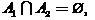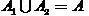(1)
Будем отождествлять двухклассовый классификатор с бинарной функцией вида
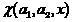
(2)
где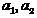 
— случайные выборки-подмножества 
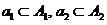из классов 
, 
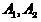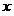-исследуемый объект, который необходимо отнести к одному из классов. Значения этой функции будут истолковываться в качестве «решений» в соответствии с правилом
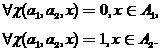
(3)
В зависимости от того, соответствуют или нет решения классификатора исходному разбиению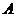 
на классы, будем считать их соответственно «правильными» или «ошибочными». Договоримся также 
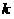-ые элементы выборок 
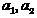обозначать 
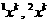, так, что соответственно:
,
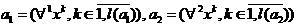(4)
где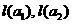 
— объемы обучающих выборок. Полагаем множество 
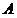«погруженным» в 
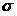-мерное правостороннее евклидово пространство 
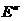. Тогда все элементы классов 
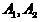, включая, естественно, и элементы обучающих выборок и исследуемый объект, можно рассматривать как его точки. Координаты объектов-точек из множества 
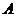будем помечать правым нижним индексом 
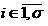. Координаты объектов 
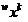обучающих выборок запишутся как 
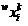, исследуемого объекта 
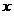как -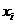
. В зависимости от контекста, 
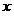понимается либо как имя объекта, либо как радиус-вектор.
Исходим из отсутствия проверочной последовательности, а оценки вероятности ошибки классификации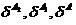 
осуществим в режиме скользящего экзамена
,
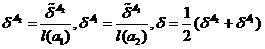(5)
где
,
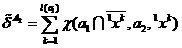(6)
.
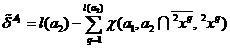(7)
Объекты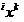 
обучающих выборок, классифицируемые в режиме скользящего экзамена, будем в дальнейшем называть квазиэкзаменируемыми.
Скорректированный скользящий экзамен
Скользящий экзамен, как известно, отличает ряд недостатков. Эти недостатки могут быть в какой-то мере устранены через коррекцию скользящего экзамена. Скорректированные оценки, помечаемые левым штрихом, запишутся следующим образом
,
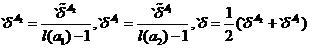(8)
,
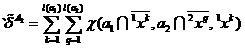(9)
.
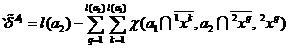(10)
К недостаткам скорректированного скользящего экзамена следует отнести возрастание количества операций и в тот факт, что эта оценка проводится на обеих выборках на единицу меньшего объема. Таким образом при малых выборках оценка вероятности ошибки оказывается несколько завышенной, однако с возрастанием объема выборок этот эффект утрачивает значение.
Соклассификатор
Вследствие большой трудоемкости скорректированного скользящего экзамена, представляет интерес метод бинарной оценки надежности классификации – соклассификатор. Как и скользящий экзамен, он может базироваться и исключительно на информации из обучающих выборок, но может использоваться и при наличии проверочных последовательностей.
Введем выборки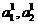 
объектов, соответственно правильно и ошибочно отнесенных классификатором (2) в режиме скользящего экзамена
,
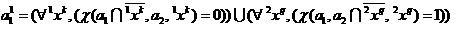(11)
.
(12)
Тогда решение соклассификатора первого порядка классификатора (2), определяемого как
,
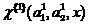(13)
истолковывается следующим образом
если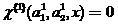 
то классификатор (2) принял правильное решение относительно 
,
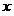если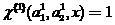 
, то классификатор(2) принял ошибочное решение относительно 
.
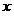(14)
При этом будем считать, что выборки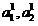 
извлечены из неких классов 
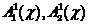объектов, потенциально правильно либо ошибочно отнесенных классификатором (2).
При определении (13) предполагается, что объем выборки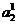 
не слишком мал. Таким образом, если располагаем лишь материалом обучающих выборок, а проверочные последовательности отсутствуют, то использовать соклассификатор рекомендуется в условиях, когда классификатор (2) допускает значительное количество ошибок. Если все же использовать соклассификатор в условиях малой выборки 
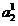, то его следует выбирать в достаточно простой форме. Например, если соклассификатор фишеровского типа, можно предположить диагональность ковариационной матрицы или даже ее единичность.
Подобно adaptive boosting, композиция классификаторов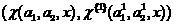 
может рассматриваться как коллективный классификатор, организованный существенно более нелинейно по сравнению с предложенными в [1].
Остановимся на вопросах, связанных с выбором конкретной формы соклассификатора. Пусть, например, выборки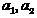 
извлечены из классов 
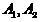с плотностями распределений 
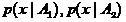, причем классы сильно перекрываются. В этом случае зачастую может оказываться, что выборочные плотности 
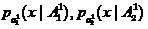имеют близкие средние значения. В этом случае соклассификатор 
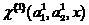может быть выбран, например, в форме линейного фишеровского классификатора, модифицированного с использованием процедуры Петерсона-Маттсона [2,3].
Фрактальный классификатор
Процесс синтеза соклассификаторов более высоких порядков может быть продолжен в рамках рекуррентной процедуры, когда первоначально осуществляется подстановка
,
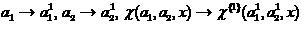(15)
затем, повторяя вышеописанный алгоритм, получаем на выходе соклассификатор второго порядка
.
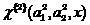(16)
и продолжаем эту процедуру. Императивный останов наступает при построении соклассификатора такого порядка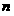 
, при котором 
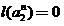или даже 
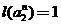. В результате получаем итерированную систему классификаторов – фрактальный классификатор. Этот коллективный классификатор не следует, разумеется, смешивать с классификаторами изображений, использующими для их обработки фрактальные и вейвлетные преобразования.
На практике нам приходилось использовать лишь соклассификаторы первого порядка. Они были разработаны нами много лет назад и зарекомендовали себя в качестве полезных инструментов при решении различных практических задач, в частности, при анализе отраженных радиосигналов для установок поиска пластиковых противопехотных мин [4], а также при создании системы LEKTON. Эта система позволила полностью автоматически проверять подлинность подписей на чеках, векселях и других документах и явилась первой реально используемой в банке системой такого типа.
Локальная вероятность ошибки
В практических исследованиях хорошо себя зарекомендовали локальные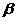 
— оценки вероятности ошибки классификации. Пусть классификатор (2) может быть представлен в форме
,
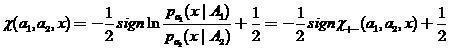(17)
где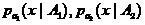 
— оценки плотностей 
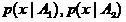по выборкам 
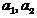соответственно. Тогда локальная 
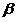— оценка вероятности ошибки этого классификатора может быть определена как
,
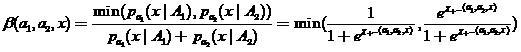(18)
где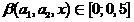 
.
Введем специальную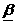 
— оценку, которая может рассматриваться в качестве «размытого» классификатора
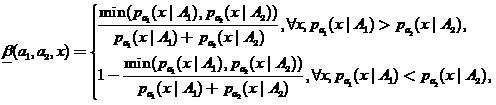
(19)
где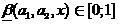 
. Тогда будем считать, что 
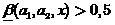истолковывается как решение размытого классификатора, что 
, 
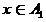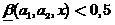— как решение, что 
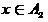. При этом, чем ближе 
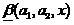к нулю либо к единице, тем соответственные решения размытого классификатора более заслуживают доверия.
На основе оценки (19) можно обобщить определение классификатора (2), введя зону отказа либо зоны отказа. Обозначая ширину этих зон соответственно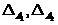 
, представим их в следующей форме
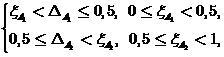
(20)
где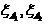 
— границы зон. При отсутствии асимметрии в требованиях к зонам выбирается 
.
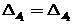Литература:
1. Archipov G. F. Collectives of determinative rules: optimal solutions and some of the characteristics of reliability of classification. – In the Collection of articles “Statistical problems of control”, Vilnius, 1983, vol.61, pp. 130-145.
2. Мясников В.В. O модификациях метода построения линейной дискриминантной функции, основанного на процедуре Петерсона-Маттсона. computeroptics.smr.ru/KO/PDF/KO26/KO26211.pdf.
3. Фукунага К. Введение в статистическую теорию распознавания образов. М. «Наука» 1979. стр. 105-130.
4. Archipov G., Klyshko G., Stasaitis D., Levitas B., Alenkowicz H., Jefremov S. Research of Metallic and Dielectric Underground Objects on the Basis of Original Computer Recognition Technique of Reflected Radio Signals. MIKON-2000., XII International Conference on Microwaves, Radar and Wireless Communications, Volume 2, pp. 495-498./>
Автор: GeorgijArchipov
