Нечеткий поиск строк является весьма дорогостоящей в смысле вычислительных ресурсов задачей, особенно если вам необходима высокая точность получаемых результатов. В статье описан алгоритм нечеткого поиска в словаре, который обеспечивает высокую скорость поиска при сохранении 100% точности и сравнительно низком потреблении памяти. Именно автомат Левенштейна позволил разработчикам Lucene повысить скорость нечеткого поиска на два порядка
Введение
Нечеткий поиск строк в словаре является основой для построения современных систем проверки орфографии, которые используются в текстовых редакторах, системах оптического распознавания символов и поисковых системах. Кроме того, нечеткий поиск находит применение при решении ряда вычислительных задач биоинформатики.

Формальное определение задачи нечеткого поиска в словаре можно сформулировать следующим образом. Для заданного поискового запроса W необходимо выбрать из словаря D подмножество P всех слов, мера отличия которых р от поискового запроса не превышает некоторого порогового значения N:
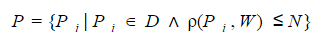
Степень отличия двух слов может быть измерена, например, при помощи расстояния Левенштейна или Дамерау-Левенштейна.
Расстояние Левенштейна это мера отличия двух строк, определяемая как минимальное количество операций вставки, удаления и замены символов, необходимых для перевода одной строки в другую.
При расчете расстояния Дамерау-Левенштейна допускаются также транспозиции (перестановки двух соседних символов).

Несколько лет назад на Хабре уже был пост от ntz посвященный нечеткому поиску в словаре и тексте — подробнее о расстояниях Левенштейна и Дамерау-Левенштейна можно прочесть там. Я лишь напомню, что временная сложность проверки условия
р(Pi, W)<=N при помощи методов динамического программирования оценивается как
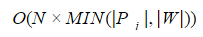 ,
,
где |Pi|,|W| — длина строки и запроса соответственно. Поэтому при решении практических задач полный перебор значений словаря с проверкой каждого слова, как правило, неприемлем.
Следует отметить, что не каждый алгоритм нечеткого поиска обеспечивает нахождение по запросу W абсолютно всех слов из словаря D, удовлетворяющих условию р(Pi, W)<=N. Поэтому есть смысл говорить о точности поиска как об отношении количества найденных результатов к действительному количеству слов в словаре, удовлетворяющих заданному условию. Например, точность поиска методом n-грамм автор уже упомянутого мной поста оценил в 65%.
Недетерминированный автомат Левенштейна
Автор предполагает, что читатель знаком с основами теории автоматов и формальных языков и воздержится от изложения терминологии этой предметной области. Вместо этого я сразу перейду к делу.
Для решения практических задач используется детерминированный конечный автомат Левенштейна (если быть до конца точным — то его имитация). Однако, чтобы понять принципы работы детерминированного конечного автомата Левенштейна, лучше предварительно рассмотреть работу недетерминированной версии.
Автоматом Левенштейна для слова W будем называть конечный автомат AN(W), принимающий слово S тогда и только тогда, когда расстояние Левенштейна (Дамерау-Левенштейна) между словами W и S не превышает заданного значения N.
Конечный автомат Левенштейна для слова W и допустимого количества модификаций N может быть задан в виде упорядоченной пятерки элементов AN(W)=<E,Q,q0,F,V>, где:
E — алфавит автомата;
Q — множество внутренних состояний;
q0 — начальное состояние, принадлежит множеству Q;
F — множество заключительных, или конечных состояний
V — функция переходов, определяющая в какое (какие) состояния возможен переход из текущего состояния при поступлении на вход автомата очередного символа.
Состояния недетерминированного автомата Левенштейна AN(W) принято обозначать как i#e, где i=0..|W|, e=0..N. Если автомат находится в состоянии i#e, это говорит о том, что в автомат введено i “корректных” символов и обнаружено e модификаций. Поскольку мы рассматриваем автомат, который поддерживает транспозиции (т.е в качестве р(S,W) используется расстояние Дамерау-Левенштейна), то множество состояний должно быть дополнено состояниями {iT#e}, где i=0..|W|-1, e=1..N.
Начальным состоянием автомата является состояние 0#0.
Множество заключительных состояний включает в себя такие состояния i#e, для которых выполняется условие |W| — i <= N — e.
Исходя из физического смысла состояний автомата, нетрудно определить состав допустимых переходов. Функция переходов автомата Левенштейна задается в виде таблицы.
Если вам интересно строгое математическое обоснование состава состояний автомата и других вышеизложенных тезисов, вы можете найти его в статье Шульца и Михова (2002).
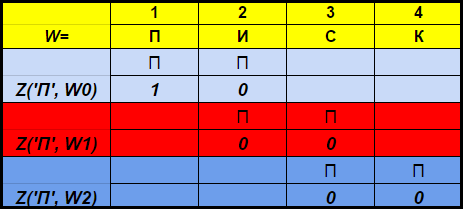
Характеристическим вектором Z(x, Wi) для символа x называется битовый вектор длины min(N + 1, |W| — i), k-й элемент которого равен 1, если (i+k)-й символ строки W равен x, и 0 в противном случае. Например, для W=”ПИСК”
Z(‘П’, W0 ) = <1, 0>, а Z(‘П’, W1 ) = <0, 0>.
Графическое представление автомата Левенштейна для W=”ПИСК” и N=1 приведено на рисунке. Переходы автомата подписаны соответствующими им характеристическими векторами.
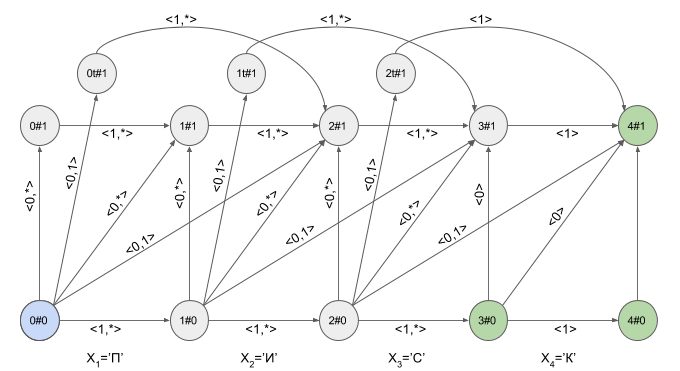
Зеленым цветом выделены конечные состояния автомата. Светло-синим — текущее (активное) состояние автомата.
Переход по горизонтальным стрелкам осуществляется тогда, когда в автомат введен “корректный” символ.
Переход по вертикальным стрелкам соответствует предположению о том, что очередной введенный в автомат символ вставлен в исходное слово W перед (i+1)-м символом. При переходе по вертикальным стрелкам автомат “обнаруживает” модификацию слова W — значение e при этом увеличивается на 1.
Переход из состояния i#e в состояние (i+1)#e+1 соответствует предположению о том, что очередной символ заменяет (i +1)-й символ в слове W.
Переход из состояния i#e в состояние (i + 2)#e+1 соответствует предположению о том, что очередной символ соответствует (i + 2)-му символу в слове W, а (i + 1)-й символ слова W пропущен в слове S.
Наверное, вы уже догадались, что переход в состояние iT#e предполагает, что обнаружена транспозиция (i + 1)-го и (i + 2)-го символов слова W.
Теперь давайте посмотрим как это работает. Ввод в автомат нового символа я буду обозначать изогнутой красной стрелкой, а справа от стрелки указывать значение характеристического вектора. Вот так автомат A1(«ПИСК») будет работать при вводе в него слова “ПОИСК”.
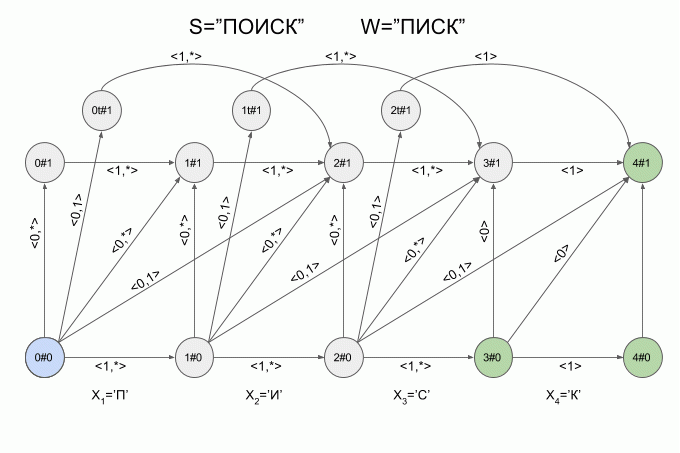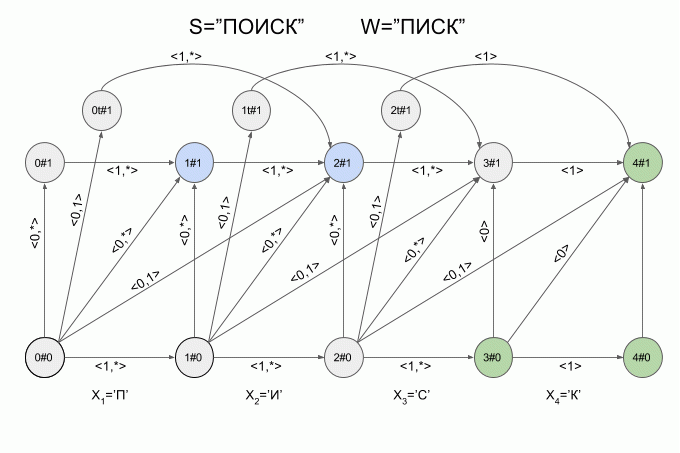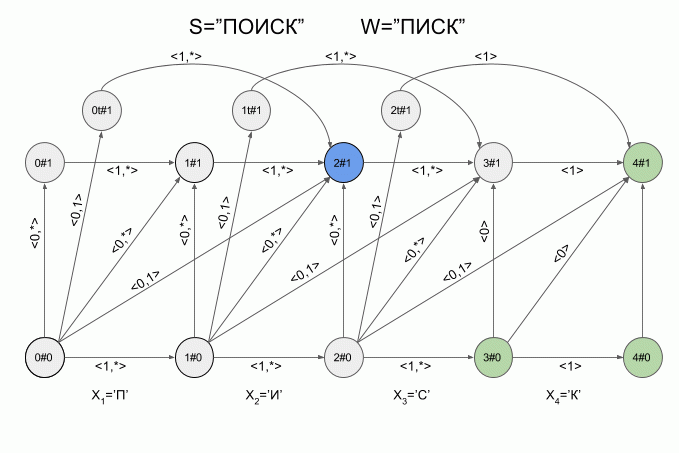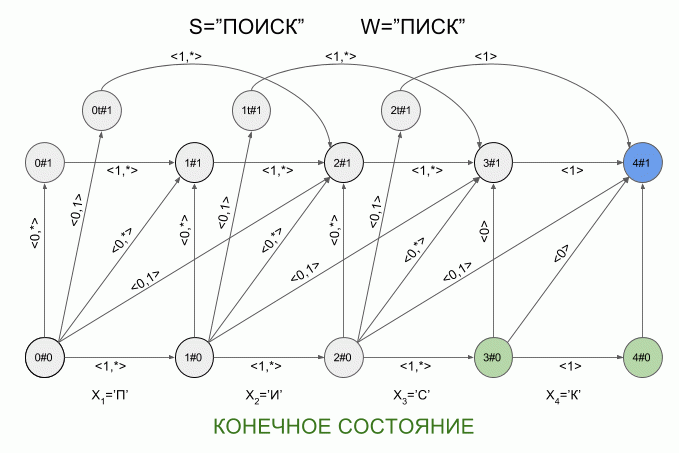
Обратите внимание, фактически последовательность смены состояний автомата определяется не конкретным словом, подаваемым на вход автомата, а лишь последовательностью характеристических векторов. Эта последовательность может оказаться одинаковой для двух разных слов. Например, если автомат настроен на слово “мама”, то последовательность характеристических векторов будет одинаковой для слов “лама”, “рама”, “дама” и т.п.
Другой интересный факт состоит в том, что структура допустимых переходов автомата не изменяется для i=0..|W| — (N+1).
Эти два обстоятельства делают возможным при программной реализации алгоритмов нечеткого поиска использовать не рассчитываемый для каждого конкретного слова автомат, а его универсальную имитацию. Именно поэтому в заголовке поста идет речь об “универсальном” автомате Левенштейна.
Расчет автомата для конкретного слова S сводится в этом случае к простому расчету характеристических векторов для каждого символа x слова S. Смена состояний программно реализуется как простое увеличение двух переменных e, i на определяемую по универсальным таблицам величину. Шульц и Михов (2002) показали, что расчет всех характеристических векторов для слова S может быть произведен за время O(|S|). Это и есть временная сложность работы автомата.
Символы слова S последовательно подаются на вход автомата. Если после подачи некоторого символа становится понятно, что расстояние между строками S и W превышает пороговое значение N, то автомат оказывается в “пустом” состоянии — активные состояния у автомата отсутствуют. В этом случае необходимость расчета характеристических векторов для оставшихся символов слова S отпадает.
Вот так автомат “отработает” слово S=”ИКС” при W=”ПИСК”:
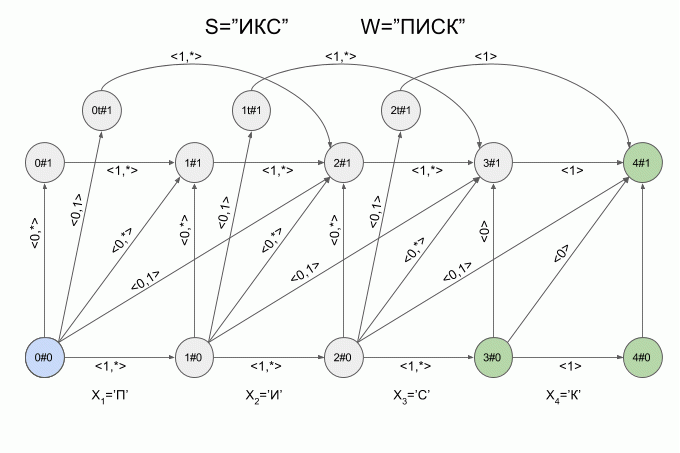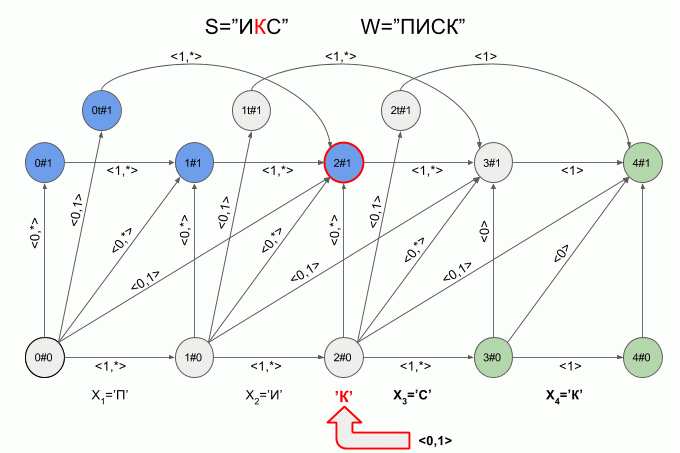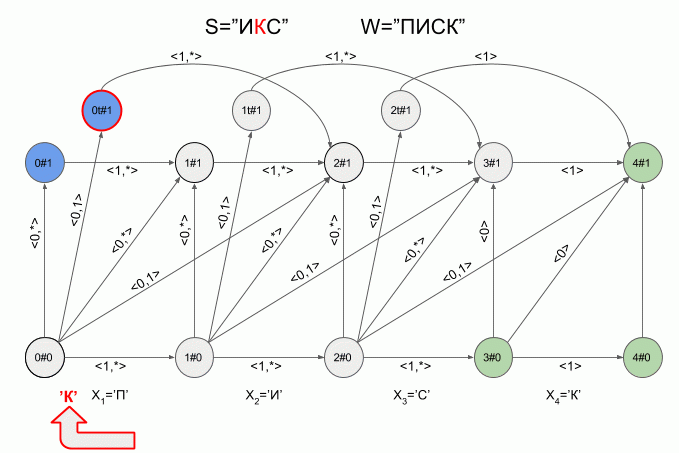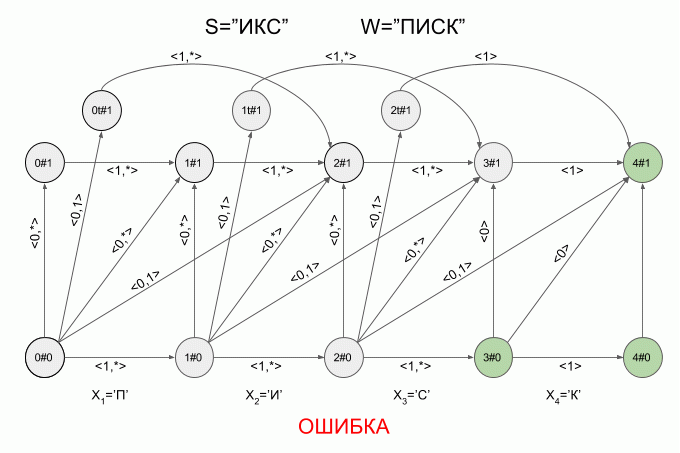
После ввода символа “И” в автомате появилось сразу четыре активных состояния, однако уже после ввода символа “К” активных состояний не осталось — автомат оказался в состоянии ошибки и не принял слово “ИКС”. При этом расчет характеристических векторов для символа “С” не осуществлялся.
Детерминированный автомат Левенштейна
В соответствии с теоремой о детерминизации для любого недетерминированного конечного автомата может быть построен эквивалентный ему детерминированный конечный автомат. Зачем нам нужен детерминированный автомат? Просто при программной реализации он будет работать быстрее. Главным образом за счет того, что может иметь всего одно текущее состояние и, как следствие, при вводе очередного символа будет необходимо рассчитывать только один характеристический вектор и определять только один переход по таблице переходов.
Если для рассмотренного выше недетерминированного автомата Левенштейна А1(W) последовательно перебрать все возможные значения характеристических векторов, то можно убедиться, что одновременно активными могут быть состояния, составляющие одно из следующих множеств:
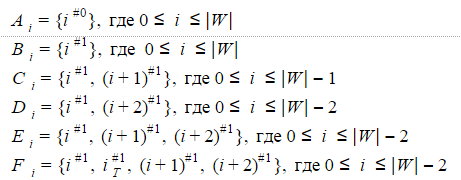
Шесть вышеперечисленных множеств и будут представлять собой состояния детерминированного автомата Левенштейна для N=1. Точнее автомат будет иметь по шесть состояний для i=0..|W|-2, три состояния для i=|W|-1 и еще два состояния для i=|W|.
Размерность характеристического вектора для детерминированного автомата может быть вычислена как 2N+1. Тогда таблица переходов автомата для слова из |W| букв при N=1 должна иметь 22x1+1 строк и 6x(|W|-1)+3+2 столбцов (например, 8х35 для слова из 6 букв). Кроме того, такую таблицу придется рассчитывать для каждого значения |W| отдельно. Это не очень удобно и требует дополнительного времени для расчета или дополнительной памяти для хранения.
Однако, как я уже писал выше, состав допустимых переходов автомата не меняется для i=0..|W| — (2N + 1). Поэтому при программной реализации гораздо удобнее имитировать детерминированный автомат вместо расчета реального. Для этого достаточно хранить значение смещения i и использовать универсальную таблицу переходов с восемью строками и шестью столбцами. Такую таблицу можно рассчитать заранее.
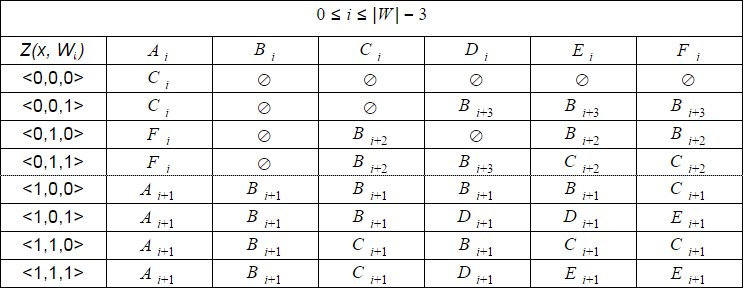
По мере увеличения i некоторые состояния автомата становятся недостижимыми, поэтому для i=|W|-2..|W| должны быть предусмотрены отдельные таблицы меньшего размера.
Далее, говоря о детерминированном автомате Левенштейна я буду подразумевать именно вышеописанную универсальную имитацию.
С увеличением N количество состояний растет по экспоненте. Так, для N=2 детерминированный автомат может иметь 42 состояния, для N=3 уже несколько сотен. А значит и потребление памяти будет пропорционально O(N2).
Начальным состоянием детерминированного автомата Левенштейна будет являться состояние A0.
Какие состояния будут конечными? Те, которым соответствуют конечные состояния недетерминированного автомата. Для N=1 это будут состояния A|W|, B|W|, A|W|-1, C|W|-1, D|W|-2, E|W|-2, F|W|-2.
Поскольку количество переходов между шестью состояниями весьма велико, а физический смысл состояний детерминированного автомата Левенштейна не очевиден, я не буду приводить здесь его графическое представление. Считаю, что картинка получается не совсем наглядной. Если вы все-таки хотите её увидеть, то можете найти в статье Михова и Шульца (2004). Я же приведу еще один пример работы недетерминированного автомата, но на этот раз буду указывать в каком состоянии в каждый момент находится его детерминированный эквивалент.
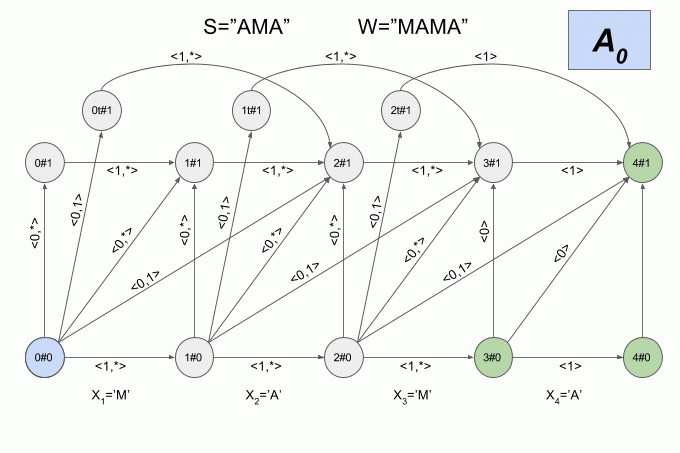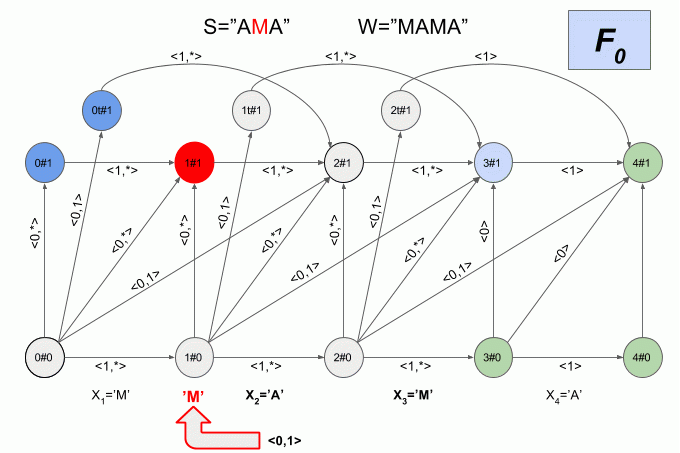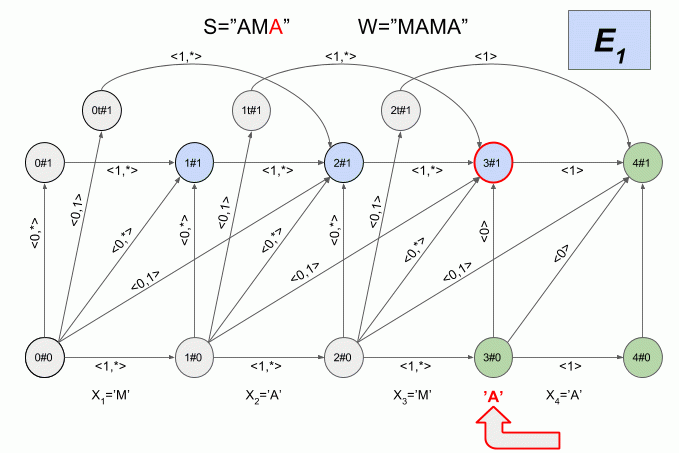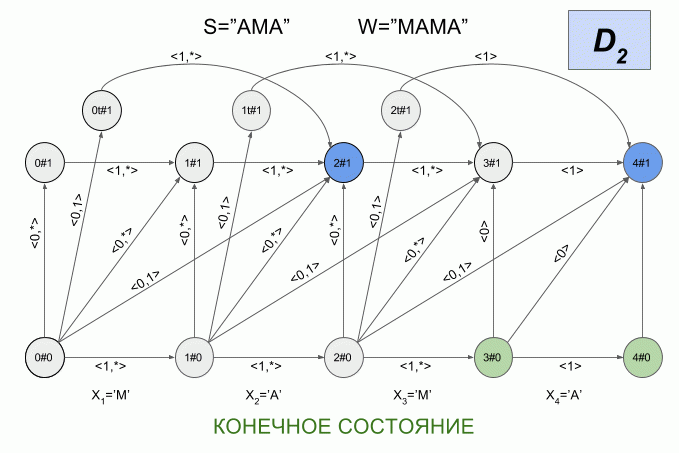
Программная реализация детерминированного автомата Левенштейна
Программную реализацию автомата Левенштейна я написал на C# — мне наиболее привычен этот язык. Исходники вы можете найти здесь. Универсальные таблицы переходов реализованы в виде полей статического класса ParametricDescription. В классе представлены универсальные таблицы переходов для N=1,2.
Помимо таблиц переходов, класс ParametricDescription содержит также таблицы инкремента смещения. Инкремент смещения — это величина, на которую нужно увеличить значение i при переходе в следующее состояние.
Сам автомат Левенштейна реализован в классе LevTAutomataImitation. Все методы класса весьма просты и я не буду описывать их подробно. При выполнении нечеткого поиска в словаре достаточно создавать один экземпляр класса на запрос.
Обратите внимание — создание экземпляра класса LevTAutomataImitation выполняется за малое постоянное время для любых значений W, S, N. В экземпляре класса хранится лишь значение W и вспомогательные переменные малого размера.
Чтобы отобрать из массива строк только те строки, которые отстоят от заданной на расстояние Дамерау-Левенштейна не более 2, вы можете использовать следующий код:
//Misspelled word
string wordToSearch = "fulzy";
//Your dictionary
string[] dictionaryAsArray = new string[] { "fuzzy", "fully", "funny", "fast"};
//Maximum Damerau-Levenstein distance
const int editDistance = 2;
//Constructing automaton
LevTAutomataImitation automaton = new LevTAutomataImitation (wordToSearch, editDistance);
//List of possible corrections
IEnumerable<string> corrections = dictionaryAsArray.Where(str => automaton.AcceptWord(str));
Приведенный код реализует простейший алгоритм нечеткого поиска в словаре с использованием автомата Левенштейна — алгоритм полного перебора. Конечно же, это не самый эффективный алгоритм. О более эффективных алгоритмах поиска с использованием автомата Левенштейна я расскажу во второй части статьи.
Ссылки
- Исходные коды к статье на C#
- Расстояние Левенштейна
- Расстояние Дамерау-Левенштейна
- Конечный автомат
- Хороший пост о нечетком поиске в словаре и тексте
- Краткое описание автомата Левенштейна
- Подробное математическое описание автомата Левенштейна в статье Шульца и Михова (2002)
- Еще одна статься Михова и Шульца (2004) на ту же тему
- История внедрения автомата Левенштейна в нечеткий поиск Lucene
Автор: IBendrup






