Вы, наверное, слышали о Дэвиде Хаффмане и его популярном алгоритме сжатия. Если нет, то предлагаю вам самостоятельно поискать в интернете — в этой статье я не буду донимать вас уроками истории или математики. Я попробую показать вам на практике, как применить этот алгоритм к текстовой строке. Наше приложение просто сгенерирует значения кода для символов из введенной строки и наборот — воссоздаст оригинальную строку из представленного кода.
Идея кодирования по Хаффману основана на использовании частоты употребления символов в строке. Наиболее часто встречающемуся символу нужно выдать как можно более короткое кодовое значение, а наименее часто встречающемуся — как можно более длинное. Из-за того, что при архивации наиболее часто встречающиеся символы должны занимать меньше места, чем раньше, а наименее часто встречающиеся могут занимать и больше места — раз их мало, то это не сильно повлияет на результат.
Для нашего примера я решил сделать символ 8-битным, т.е. типа char. С тем же успехом можно было выбрать длину и в шестнадцать, десять или двадцать битов. Длину символа стоит выбирать в зависимости от ожидаемых входных данных. Например, для кодирования видеофайлов я бы выбрал символ того же размера, что и пиксель. Имейте в виду, что увеличение или уменьшение длины символа влияет на длину кода для каждого из символов — ведь чем больше длина, тем больше символов этой длины может существовать: способов записать единицы и нули в восемь бит гораздо меньше, чем в шестнадцать. Поэтому длину символа нужно регулировать в зависимости от задачи.
Алгоритм Хаффмана активно задействует бинарные деревья и очереди с приоритетом, так что, если вы с ними не знакомы, придется для начала восполнить пробелы в знаниях.
Пусть у нас есть строка «beep boop beer!», которая занимает в памяти 15*8=120 битов. После кодировки по Хаффману этот размер удастся сократить до 40 битов. Если придираться к деталям, на экран мы выведем строку, состоящую из 40 элементов типа char (нули и единицы), а чтобы она занимала ровно 40 битов в памяти, эту строку нужно конвертировать в биты с использованием операций двоичной арифметики, которые мы не будем здесь рассматривать подробно.
Итак, рассмотрим строку «beep boop beer!». Чтобы сконструировать кодовые значения для всех элементов в зависимости от их частоты, нужно построить такое бинарное дерево, в котором каждый лист содержит символ из данной строки. Дерево мы будем строить от листьев к корню, чтобы элементы с меньшей частотой находились дальше от корня, а более часто встречающиеся — ближе к нему. Скоро узнаете, почему.
Для строительства такого дерева воспользуемся очередью с приоритетом, но немного модифицированной — инвертируем приоритеты, чтобы элемент с наименьшим приоритетом был самым важным. Получается, очередь сначала будет возвращать элементы с наименьшей частотой. Эта модификация поможет нам построить дерево начиная с листьев.
Для начала посчитаем частоту каждого символа:
| Символ | Частота |
|---|---|
| ‘b’ | 3 |
| ‘e’ | 4 |
| ‘p’ | 2 |
| ‘ ‘ | 2 |
| ‘o’ | 2 |
| ‘r’ | 1 |
| ‘!’ | 1 |
После этого создадим элементы бинарного дерева для каждого символа и представим их как очередь с приоритетом, в качестве которого будем использовать частоту.
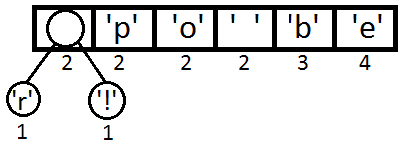
Теперь возьмем первые два элемента из очереди и создадим третий, который будет их родителем. Этот новый элемент поместим в очередь с приоритетом, равным сумме приоритетов двух его потомков. Иначе говоря, равным сумме их частот.
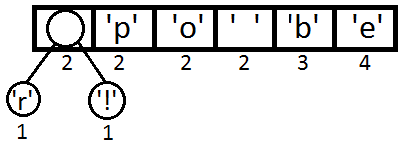
Далее будем повторять шаги, аналогичные предыдущему:
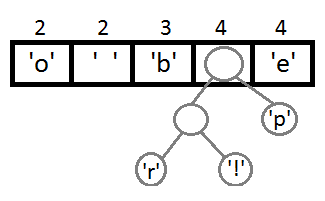
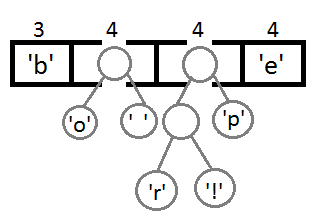
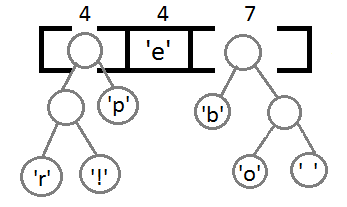
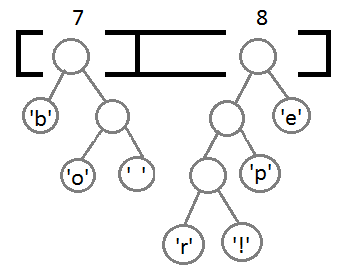
Теперь, после объединения последних двух элементов с помощью их нового родителя, мы получим итоговое бинарное дерево:
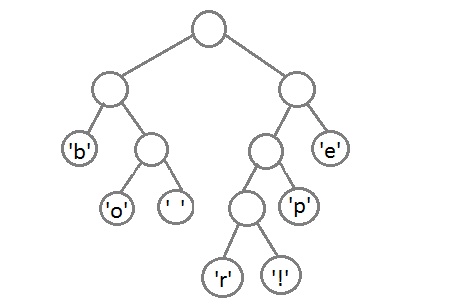
Осталось присвоить каждому символу его код. Для этого запустим обход в глубину и каждый раз, рассматривая правое поддерево, будем записывать в код 1, а рассматривая левое поддерево — 0.
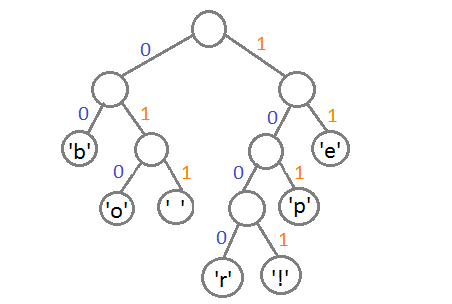
В результате соответствие символов кодовым значениям получится следующим:
| Сивол | Кодовое значение |
|---|---|
| ‘b’ | 00 |
| ‘e’ | 11 |
| ‘p’ | 101 |
| ‘ ‘ | 011 |
| ‘o’ | 010 |
| ‘r’ | 1000 |
| ‘!’ | 1001 |
Декодировать последовательность битов очень просто: нужно обходить дерево, отбрасывая левое поддерево, если встретилась единица и правое, если встретился 0. Продолжать обход нужно до тех пор, пока не встретим лист, т.е. искомое значение закодированного символа. Например, закодированной строке «101 11 101 11» и нашему дереву декодирования соответствует строка «pepe».
Здесь важно заметить, что ни одно кодовое значение не является префиксом никакого другого. В нашем примере 00 — код символа «b». Это значит, что 000 уже не может быть кодом ни для какого другого символа, т.к. иначе это привело бы к конфликту при декодировании. Ведь если после прохода по 00 мы пришли к листу «b», то по кодовому значению 000 мы уже не найдем никакого другого символа.
На практике после генерации дерева Хаффмана нужно сконструировать также таблицу Хаффмана. Таблица (в виде связного списка или массива) сделает процедуру кодирования более эффективной, ведь искать символ в дереве и одновременно записывать его код — неоправданно трудоемко. Поскольку мы не знаем наверняка, где находится этот символ, в худшем случае придется в его поисках перебрать все дерево. Как правило, для кодирования используют таблицу Хаффмана, а для декодирования — дерево Хаффмана.
Входная строка: beep boop beer!
Входная строка в двоичном виде: 0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 0001
Закодированная строка: 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001
Нетрудно заметить значительную разницу между ASCII-кодировкой строки и ее же видом в коде Хаффмана.
Необходимо отметить, что статья только объясняет только принцип работы алгоритма. Для практического применения вам придется добавить дерево Хаффмана в начало или конец закодированной последовательности. Получатель сообщения должен знать, как отделить дерево от содержания и как восстановить его из текстового представления. Хороший способ для этого — обходить дерево в любом заранее выбранном порядке, записывая 0 для каждого встреченного элемента, не являющегося листом, и 1 для каждого листа. Вслед за единицей можно записать исходный символ (в нашем случае — типа char, 8 бит в кодировке ASCII). Дерево, записанное в таком виде, можно поместить в начале закодированной последовательности — тогда получатель, в самом начале разбора построив дерево, уже будет знать, как ему декодировать записанное далее сообщение и получить из него оригинал.
Прочитать о более продвинутой версии алгоритма вы можете в статье "Адаптивное кодирование Хаффмана".
P.S. (от переводчика)
Спасибо bobuk за то, что дал ссылку на исходную статью в своем линкблоге.
Автор: mkaz