В отечественной и зарубежной аэродинамике уже несколько десятилетий находит применение метод дискретных вихрей (МДВ) для расчёта характеристик некоторых аэродинамических объектов. И хотя, с ростом вычислительных возможностей, на передний план вышли более точные методы, реализованные в многочисленных CFD-пакетах, старый добрый МДВ всё-таки имеет свою узкую, но востребованную нишу в аэродинамических исследованиях.
Попытаемся дать обзор нашему старичку, может быть даже не с точки зрения практики его применения, а как пример того, как некоторые, казалось бы, чисто математические абстракции, поселившиеся в головах умных людей, могут описывать реальные физические явления.
Начнём с того тезиса, что вся аэродинамика, как наука о движении тел в газовой среде, в принципе сводится к получению двух компонент сил, действующих в каждой точке поверхности этих тел (Ну если нас не очень интересуют красивые картинки белых следов за современными истребителями при сложном пилотаже или сердечки в облаках за гражданским лайнером). Эти компоненты – касательная и нормальная составляющие к поверхности тела. Не углубляясь в долгие объяснения, можно просто констатировать, что два указанных компонента зависят от полей параметров омывающей газовой среды: скоростей, давления и плотности (поле температуры также имеет место быть, но влияет не непосредственно, а через первые три). Первые два поля – векторные (давление «обнормаливаем»), третье – скалярное. Эти поля взаимосвязаны между собой известными зависимостями и задача CFD именно рассчитать данные поля, используя данные зависимости.
А теперь остановимся только на одном из полей – скорости. И посмотрим на поле скоростей, которое создаёт на двумерной плоскости такая гидродинамическая особенность, как вихрь. Одиночный вихрь – это просто скорости, рассчитанные по формуле, если не изменяет память, Био-Савара, смысл которой в том, что чем дальше точка измерения от точки вихря, тем величина скорости ниже. И формула, выражающая эту глубокую мысль, записывается так:
Где Г – это интенсивность вихря (циркуляция), а R – расстояние до его центра.
На самом деле упоминание глубокой мысли – это не совсем «шутка юмора». В этой формуле действительно есть глубокий смысл, но сейчас не будем в него погружаться, а просто нарисуем картинку векторов двумерного поля скоростей единичного вихря (красная точка).

Кстати, слово «вихрь» – это не случайно. В природных вихрях, торнадо, в горизонтальном разрезе имеет место именно такая картина скоростей.
Пока всё довольно просто. Теперь поместим несколько вихрей в ряд и посмотрим на результирующую картину поля скоростей.

С интересом обнаруживаем, что поле скоростей сформировалось таким, как будто поток обтекает некоторое вытянутое по горизонтали тело.
«А ведь это мысль!» - скажут (и сказали) наиболее догадливые представители вида «Гомо сапиенс» и попробовали заменить обтекаемое тело набором вихрей.
И заменили.
И добавили внешний набегающий поток, и применили гипотезу, что между вихрями суммарная нормальная составляющая скорости должна быть нулевой (условие «непротекания» несущей поверхности).
И написали соответствующую систему линейных алгебраических уравнений, по результатам решения которой находятся интенсивности (или циркуляции скорости) вихрей.
Ну, про то, что на седьмой день они отдыхали и, возможно, выпивали, я писать не буду, но что же в результате?
В результате для, например, приведенной ниже конфигурации вихрей получается следующая картина течения. Здесь красным цветом обозначены вихри, голубым – внешний поток, а розовым – циркуляции вихрей, представленные в виде векторов, направленных по местным нормалям к линии вихрей.

- Ничего не напоминает?
- Верно, мы в Париже, дорогой товарищ! (с) …ну то есть у нас получилась классическая картина распределения давления по профилю крыла самолёта, который находится под некоторым углом атаки.
А вот как нам рисует его интернет (не будем придираться к деталям).

И это распределение и даёт нам ту самую волшебную подъёмную силу, благодаря которой, как мы знаем, «самолёты летают и крыльями не машут».
Стоит ли говорить, что за многие годы под эти простые идеи была подведена строгая математическая база (вспоминаем одного из основоположников отечественной авиации, Николая Егоровича Жуковского), отдельные вихри трансформировались в тонкие несущие поверхности, появились вихревые следы и всё вместе превратилось в тот самый МДВ, о котором наш рассказ.
Профессионалы CFD могут обоснованно заметить, что пакеты, основывающиеся на решении более полных и сложных уравнений движения газа, дают гораздо более точный и многомерный результат и с этим никто не будет спорить. Просто приведём пару примеров, когда МДВ «дёшево и сердито» с приемлемой достоверностью решал задачи, для которых в CFD-программах, возможно, понадобились бы несопоставимо большие трудозатраты и вычислительные ресурсы.
Итак, в своё время в ЦАГИ был проведён натурный эксперимент, в котором исследовалось маховое движение лопастей вертолётного несущего винта.

На изображении выше - стенд МВП-8 в аэродинамической трубе Т-105, где проходило исследование. А далее дано сравнение измерений угла взмаха лопасти (черные линии) с расчётом по МДВ-программе (цветные линии).
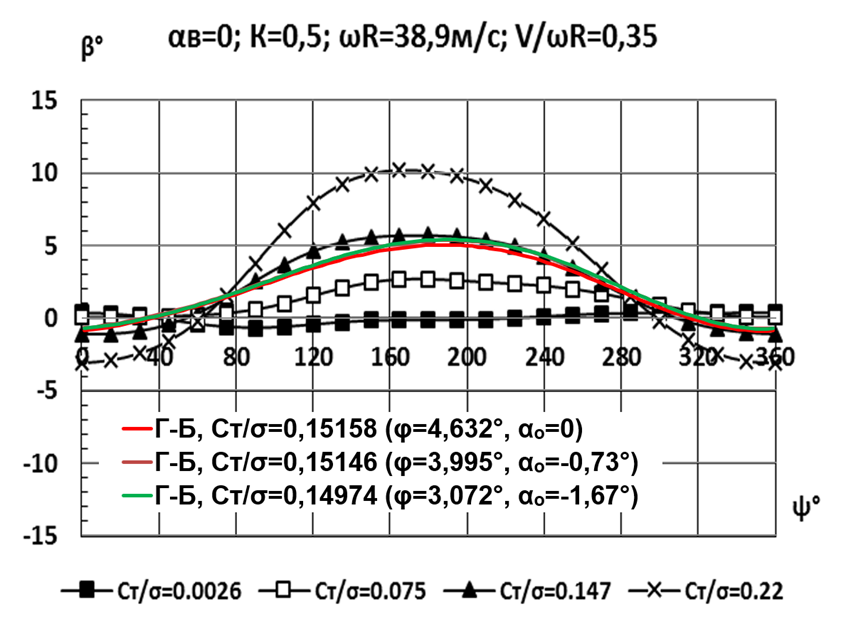
Совпадение, как видим, достаточно хорошее, а для разработчиков вертолётов данные весьма ценные.
Согласитесь, для моделирования в CFD несущий винт – объект достаточно сложный и трудоёмкий. Вспомнить хотя бы о количестве степеней свободы движущейся вертолётной лопасти. Автору же МДВ-программы понадобилось несколько часов, чтобы задать геометрические, кинематические и массо-инерционные характеристики лопасти и провести расчёты нескольких вариантов исходных данных и режимов.
Кстати, не совсем в курсе, но может быть подобные задачи на современных компьютерах уже решаются и CFD-пакетами за приемлемое время?
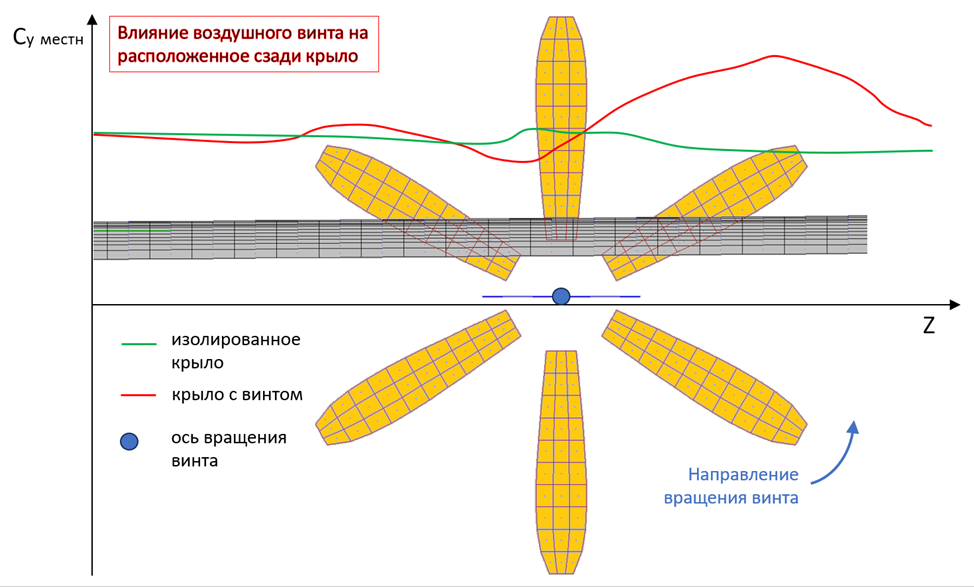
Другой пример – это случай, когда требовалось качественно и приближенно – количественно оценить влияние воздушного винта на расположенное позади него крыло. Опять-таки, не будем рассуждать, насколько эта задача трудоёмка в CFD, но результат по МДВ вполне согласуется с известными теоретическими выводами: в целом винт влияет на крыло положительно, увеличивая его подъёмную силу, но надо знать, где его располагать, потому что струя от винта имеет сложную пространственную конфигурацию, и может «работать» как позитивно, так и не очень.
В общем, несерьёзный очерк о серьёзной вещи как бы закончен. Если кто-то обнаружил слишком легкомысленное и неполное отношения к материалу – просьба не сильно ругаться, автор не ставит перед собой фундаментальных научных и научно-просветительских задач.
Автор: Rishat822