Что общего у этой картинки, Excel и прикладной работы с базами данных? Правильно — байесовский подход к анализу данных.
Если я не заинтриговал вас картинкой выше, то давайте я расскажу вам самую малость про байесовы сети и как использовать их на коленке (и почему их мало используют на практике). Этот предмет довольно технический (вот условно бесплатный курс от Стенфорда, он немного скучноват и очень технический, но зато в тему. Там еще есть странность — пройти курс и все понять можно за 10 часов, а чтобы решить задачи в матлабе, нужно часов 50 — такое ощущение, что задачи — это PhD автора курса...).
0. Немного теории
In a nutshell, простыми словами, байесовы модели — это набор вероятностных распределений (пардон за термины), которые соединены стрелочками (ужасно звучит, но самое простое объяснение такое). В классических байесовых моделях стрелочки имеют направленность (в цепях Маркова — направления нет).
Тут также репостил ссылку про визуализацию условной байесовой вероятности.

Определение от профессора.
Если разбить модель на пальцах на составляющие, то по сути она состоит из:
- Безусловных вероятностных распределений (сумма весов в таблице равна единице) определенных случайных величин (сложность, интеллект, оценки из примера ниже);
- Условных распределений случайных величин, которые зависят от других;
- Правил, по которым можно работать с такими моделями, причинно-следственных связей и аксиоматики (смотрите курс выше);
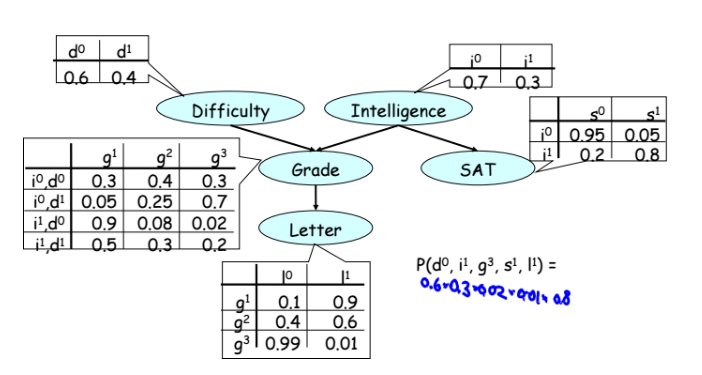
Меньше слов — больше дела. Вот пояснение in a nutshell.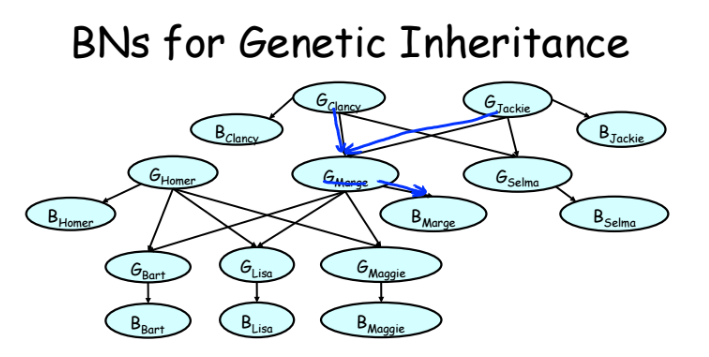
Более сложная модель на примере Симсонов.
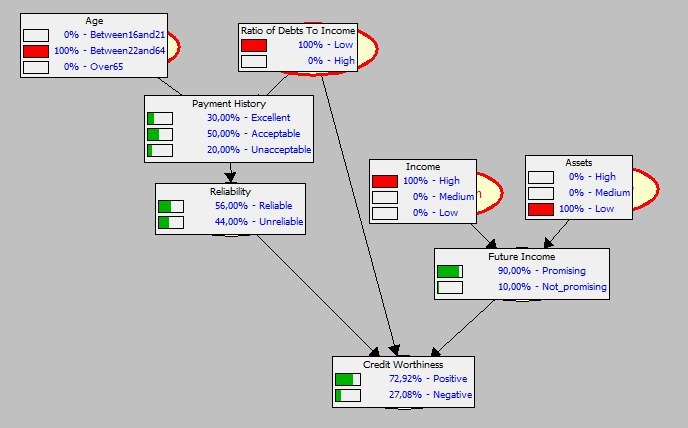
Более приближенная к реальности модель
Такие модели в строгом смысле математические и у них есть своя аксиоматика. Но с моей точки зрения интересными их делает возможность делать выводы про переменные, которые формально никак не связаны. Чтобы не лезть в дебри того, в чем я не очень разбираюсь, я просто приведу 3 примера того, как такие модели могут позволять делать простейшие выводы в реальной жизни и потом расскажу, как они помогли мне решить прикладную задачу и почему на практике они редко используются.
1. Немного логики
Пример 1 — причинно следственная связь (примеры их курса) или индукция (в математике стрелочка вправо =>). Вероятность, что у вас будет положительный отзыв (letter) при прочих равных равна примерно 50%. Если при этом вы не очень умны, то она падает до 39%. Если при этом курс простой — то вероятность опять повышается до 51%. Все это кажется простым и логичным.
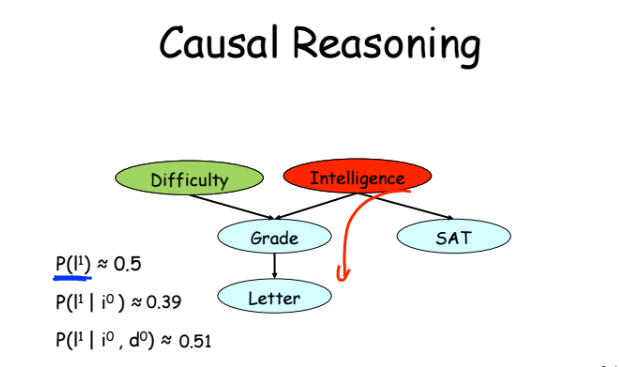
Пример 2 — дедукция (решение на основе неких данных, или стрелочка влево <=). Если студент получил тройку, то вероятность того, что он не очень умный растет, а вероятность того, что курс сложный — тоже растет.
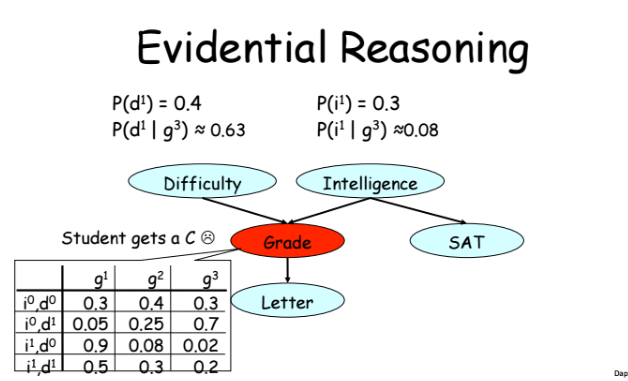
Пример 3 — самый интересный. Если мы зафиксировали, что студент получил тройку, то при росте наблюдаемой сложности предмета вероятность того, что студент умный, тоже начинает расти. Получается, что никак не связанные переменные — интеллект и сложность курса становятся связанными при условии, что у нас есть наблюдение оценки, которую получил студент. По сути это просто пример применения теоремы Байеса.
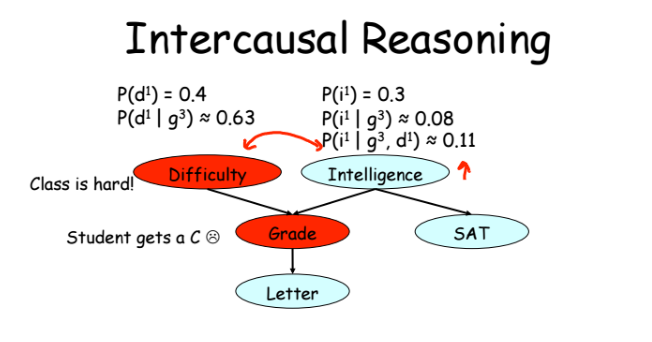
2. Немного практики
Еще пара слов, почему такие модели редко применяются в ЧИСТОМ виде в реальности:
- Количество параметров такой модели весьма высоко, и зачастую выше, чем число переменных;
- Требуется большое количество статистики по прошлым распределениям, что есть далеко не в каждой области знаний;
- Зачастую нельзя наблюдать непосредственные переменные, а можно только наблюдать логи действий людей. В описанной выше модели наблюдение оценки и сложности может заменить наблюдение интеллекта, но это все вилами на воде писано;
- Если при использовании линейной модели есть статистические тесты на значимость, а при использовании machine learning алгоритмов есть валидационная и тестовая выборка, то при использовании байесовых моделей по сути априори сразу требуется глубокое знание предметной области и много данных;
- С другой стороны — по сути любая регрессия или нейронная сеть, по логике своей является простой байесовой моделью, где закреплена некая структура данных;
А теперь соберем все это у себя в голове и применим такой подход на коленке к работе с корпоративными базами данных. Если вы довольно неплохо разбираетесь в предметной области и в том, как в реальности связаны некие переменные в ней, то ультра-простые байесовы модели на коленке могут вам позволить очень быстро делать нужные вам выводы.
Представьте, что есть некая база данных, где компания собирает 3 вещи — имя, адрес почты человека и его IP адрес. 99% веб-сервисов могут получить доступ к такой статистике. Представьте, что компания является глобальной и не имеет ограничений по географии своих клиентов и стоит задача определить язык, на котором говорит каждый человек с высокой степенью вероятности за очень краткий срок.
Конечно в идеальном мире можно было бы сделать так (в скобках пишу почему не подходит):
- Написать / позвонить части клиентов, спросив какой у них язык (а если у вас 2 часа на задачу а клиентов десятки или сотни тысяч?);
- Принять банальное предположение, что язык равен самому популярному языку в стране (а если в IP адресах много стран, где 3-4 официальных языка, и языки по-разному используются разными слоями населения и профессиями?);
- Взять язык интерфейса, который выбрали клиенты (а если они еще не успели зайти в интерфейс, и просто зарегистрировались?);
- Взять язык браузера (а что если такой лог еще тоже не сохранили или просто забыли сохранить?);
В таком случае помогает так называемое "просеивание" или подход состоящий в применении примитивных интуитивных байесовых вероятностей. Выглядит он примерно так:
- Выделяем почтовый домен из адреса почты (aveysov@gmail.com => gmail.com);
- Все ярко национальные сервисы (типа qqq или 123 в китае, mail.ru в России и тому подобное) — очень сильно говорят, что человек говорит на языке сервиса даже невзирая на имя человека или страну его последнего;
- Из оставшегося выбираем национальные субдоменты типа yahoo.de или просто национальные домены. Условная вероятность, того, что человек говорит по-немецки даже если у него последняя страна захода — США — гораздо выше, чем если у него просто страна захода — Германия;
- Из оставшегося проставляем языки для очевидных стран, где точно преобладает один государственный язык;
- Остаются страны с большим числом языком или просто очень многонациональные / многоязыковые страны;
- В таком случае в идеале дальше надо найти вектора, которые бы говорили как распределены имена по языкам, но такой статистики я быстро не смог найти и просто остановился на самом популярном языке для страны оставшихся пользователей;
3. Немного красоты
Это все прекрасно, но как сейчас проверить, что наша примитивная модель сработала? Очень просто — посмотреть на имена людей с заданным языком. Язык — как правило статистически свойство культуры (людей, которые имеют сразу 2-3 родных языка и национальности очень мало). Можно построить просто вектора вероятностей, а можно построить красивые картинки.
Арабский язык

Немецкий язык

Греческий язык

Португальский язык
Испанский язык

Китайский язык

Словенский язык

Венгерский язык

Французский

Хинди

Польский язык

Русский язык

Чешский

И внезапно английский язык (объяснение простое — если убрать страны юго-восточной Азии, то все встает на свои иместа)

Английский без стран юго-восточной Азии

Вот как-то так. За пару часов, без обучающей выборки, но с пониманием простейших байесовых моделей можно просеять любой подобный датасет и получить приемлемый результат в разрезе усилия / время / точность.
Автор: Александр