Трехмерный движок внутри запроса SQL

в 8:21, , рубрики: 3d, 3d-движок, phong, postgresql, ray marching, raymarching, sql, sqlite, аппроксимация, аппроксимация квадратного корня, вавилонский метод, затенение по фонгу, квадратный корень, любителей читать теги, магическая константа, метод герона, ненормальное программирование, погрешность, поздравляю с первой пятницей, рекурсивные запросы, трассировка лучей, трехмерный движок

Несколько лет назад на форуме SQL.ru решили провести сравнение реализаций трассировщиков лучей на разных языках программирования. К сожалению, моя заявка не может участвовать т.к. она не выводит надпись «PIXAR», поэтому публикую ее здесь.

Для чистоты эксперимента я использовал SQLite без расширений. Оказалось, что там нет даже функции SQRT.

WITH RECURSIVE numbers AS (SELECT 0 AS n UNION ALL SELECT n+1 FROM numbers WHERE n<89),
pixels AS (SELECT rows.n as row, cols.n as col FROM numbers as rows CROSS JOIN numbers as cols WHERE rows.n > 4 AND rows.n < 38 AND cols.n > 9 AND cols.n < 89),
rawRays AS (SELECT row, col, -0.9049 + col * 0.0065 + row * 0.0057 as x, -0.1487 + row * -0.0171 as y, 0.6713 + col * 0.0045 + row * -0.0081 as z FROM pixels),
norms AS (SELECT row, col, x, y, z, (1 + x * x + y * y + z * z) / 2 as n FROM rawRays),
rays AS (SELECT row, col, x / n AS x, y / n AS y, z / n AS z FROM norms),
iters AS (SELECT row, col, 0 as it, 0 as v FROM rays UNION ALL SELECT rays.row, rays.col, it + 1 AS it, v + MAX(ABS(0.7+v*x) - 0.3, ABS(0.7+v*y) - 0.3, ABS(-1.1+v*z) - 0.3, -((0.7+v*x) * (0.7+v*x) + (0.7+v*y) * (0.7+v*y) + (-1.1+v*z) * (-1.1+v*z)) * 1.78 + 0.28) AS v FROM iters JOIN rays ON rays.row = iters.row AND rays.col = iters.col WHERE it < 15),
lastIters AS (SELECT it0.row, it0.col, it0.v AS v0, it1.v AS v1, it2.v AS v2 FROM iters as it0 JOIN iters AS it1 ON it0.col = it1.col AND it0.row = it1.row JOIN iters AS it2 ON it0.col = it2.col AND it0.row = it2.row WHERE it0.it = 15 AND it1.it = 14 AND it2.it = 13),
res AS (SELECT col, (v0 - v1) / (v1 - v2) as v FROM lastIters)
SELECT group_concat(substr('$@B%8&WM#*oahkbdpqwmZO0QLCJUYXzcvunxrjft/|()1{}[]?-_+~<>i!lI;:,"^. ', round(1 + max(0, min(66, v * 67))), 1) || CASE WHEN col=88 THEN X'0A' ELSE '' END, '') FROM res;


                                :++++I
                          _________________________"
                   ------/jucYJLQ0OZmwwwwwwwmmZO0QCUXcnj----------
            ???????:<}/nzJQOwqdbkhao***####**o         LUcx|[<;????????????????
     ]]]]]]]]][[[  !{xu;    o#MW&8%BB@@@@@                -ct[l  ]]]]]]]]]]]??-
U[[[[[[[}}}}}}}}}   ;1X]      $$$$$$$$$$                  cx["   [[[[[[[[]]]??
UUJJJCCCLLL{{{{{{{{{{   :|QZzffB$$$$$$               |Qu?     {{{{{{}}}[[]]??-
YUUJJJCCCLLLQQ000OOO111111111         ,l!!;           111111111111{{}}[[]]??-
 YUUJJJCCCLLLQQQ00OOOZZZmmmwww(((((((((((((((((((()))))))))))))11{{     i]??-
 YYUUUJJCCCLLL  ?fuv|  ZZZmmmwwwqqqpppd||||||||||||||||||((())11{   i++i;??--
 YYYUUUJJJ i               Cmmwwwqqqppppdddbbbbk///////||(())11  }czfYuf{_--
  XYYUUU                       Wwwwqqqpppddddbbbbkkkk/||(()))  |j     :zr)--
  XXYYY;                         $$wqqqqpppddddbbbbk/|||(()) ^X        Jcf-
  XXXY                          $$$$xwqqqppppddddbbb/||(()) v          LX-_
   zXX!                        $$$$$$$nqqqqppppdddbb||(()) q          mQX-
   zzX>                      $$$$$$$$$$$$qqqqppppddd|(()) k          dmL-_
    zzl                     $$$$$$$$$$$$$$wqqqqppppd((() o        W*kqOJ__
    czz?                  $$$$$$$$$$$$$$$$$ wqqqqpp|(() O     $$BadmQ__
    ccc!1x             $$$$$$$$              wwqqqq(() {$$$$$$$Babw0___
     vcc<)xXQm   W%@$$$$$$                   mwwwwq()) %$$$$$@%W#adwQ___
     vvcc>1rzCZqkoM&B$$                      bmmwww)) )o$$$$B&MokpZL-__+
     uvvvcc]tuUQmpkoM                         Zmmmm)1 J-   &MohdmQU-__++
      uuvvvcc{jvUQmp                          ZZZm)11 J:    kpmQUc-__;
      nuuuvvvcc}fuYL                         nOOZZ11  /|   .0CXu}-_
        nuuvvvccc-)jv                       !00OOO11{ ;/zvzvxt1--
             vvvcccz+{                     }QQ000O1{{   !~+~>?-
                  ccczz:<]               : LQQQQ00{{}}[   ]??
                       zzzzXX  ";I;"   JCCCLLLLQQQ{}}[[]]]?
                           zzXXXYYYUUUUJJJCCCCLLL{}}[[]]]
                                XXYYYYUUUJJJJCCCC}}[[]]
                                     YYYUUUUJJJJC}[[]
                                          YUUUUJJ[[
                                               UU

Здесь можно покрутить кубик

Под катом построчный разбор запроса. Как обычно, достаточно знания основ SQL и школьной математики.

Disclaimer: я далек от мира БД, поэтому буду раз замечаниям в личку.

Версия для Postgres (почему-то выполняется на порядок дольше, чем на SQLite)

WITH RECURSIVE numbers AS (SELECT 0 AS n UNION ALL SELECT n+1 FROM numbers WHERE n<89),
pixels AS (SELECT rows.n as row, cols.n as col FROM numbers as rows CROSS JOIN numbers as cols WHERE rows.n > 4 AND rows.n < 38 AND cols.n > 9 AND cols.n < 89),
rawRays AS (SELECT row, col, -0.9049 + col * 0.0065 + row * 0.0057 as x, -0.1487 + row * -0.0171 as y, 0.6713 + col * 0.0045 + row * -0.0081 as z FROM pixels),
norms AS (SELECT row, col, x, y, z, (1 + x * x + y * y + z * z) / 2 as n FROM rawRays),
rays AS (SELECT row, col, x / n AS x, y / n AS y, z / n AS z FROM norms),
iters AS (SELECT row, col, 0 as it, 0.0 as v FROM rays UNION ALL SELECT rays.row, rays.col, it + 1 AS it, v + GREATEST(ABS(0.7+v*x) - 0.3, ABS(0.7+v*y) - 0.3, ABS(-1.1+v*z) - 0.3, -(0.28 + ((0.7+v*x) * (0.7+v*x) + (0.7+v*y) * (0.7+v*y) + (-1.1+v*z) * (-1.1+v*z)) / 0.28) / 2.0 + 0.42) AS v FROM iters JOIN rays ON rays.row = iters.row AND rays.col = iters.col WHERE it < 15),
lastIters AS (SELECT it0.row, it0.col, it0.v AS v0, it1.v AS v1, it2.v AS v2 FROM iters as it0 JOIN iters AS it1 ON it0.col = it1.col AND it0.row = it1.row JOIN iters AS it2 ON it0.col = it2.col AND it0.row = it2.row WHERE it0.it = 15 AND it1.it = 14 AND it2.it = 13),
res AS (SELECT col, (v0 - v1) / (v1 - v2) as v FROM lastIters)
SELECT string_agg(substring('$@B%8&WM#*oahkbdpqwmZO0QLCJUYXzcvunxrjft/|()1{}[]?-_+~<>i!lI;:,"^. '::text FROM round(1 + GREATEST(0, LEAST(66, v * 67)))::integer  FOR 1) || CASE WHEN col=88 THEN E'n' ELSE '' END, ''::text) FROM res;

Для понимания терминологии и принципа работы алгоритма рекомендуется ознакомиться со статьей про ray marching для Excel.

Общая структура

Список промежуточных таблиц:

  • numbers (n) – содержит числа от 0 до 89.
  • pixels (row, col) – содержит номер строки и столбца для каждого «пикселя».
  • rawRays (row, col, x, y, z) – содержит ненормализованные лучи из камеры к экрану.
  • norms (row, col, x, y, z, n) – содержит длины лучей.
  • rays (row, col, x, y, z) – содержит нормализованные лучи из камеры к экрану.
  • iters (row, col, it, v) – содержит итерации ray marching.
  • lastIters (row, col, v0, v1, v2) – содержит три последние итерации из предыдущей таблицы для каждого «пикселя».
  • res (col, v) – содержит «яркости» пикселей.

Относительно того, как они друг от друга зависят все просто: каждая следующая таблица использует только предыдущую, а финальный запрос использует только таблицу res.

Все таблицы (за исключением numbers и iters) содержат по 81 x 29 строк (по одной на каждый «пиксель»), колонки row и col индексируют их координаты. Таблица iters содержит 81 x 29 x 15 строк (по одной на каждую итерацию ray marching для каждого «пикселя»). Номер итерации содержится в колонке it.

Финальный запрос выдает таблицу из одной строки и колонки с текстом, все остальные таблицы содержат только вещественные числа (при этом колонки row, col и it – целые неотрицательные).

Получается, если опустить вспомогательные таблицы, очень простая структура запроса:

WITH RECURSIVE
  numbers AS (SELECT ...),
  pixels AS (SELECT ...),
  rawRays AS (SELECT ...),
  normsSq AS (SELECT ...),
  norms AS (SELECT ...),
  rays AS (SELECT ...),
  iters AS (SELECT ...),
  lastIters AS (SELECT ...),
  res AS (SELECT ...)

SELECT group_concat(substr('$@B%8&WM#*oahkbdpqwmZO0QLCJUYXzcvunxrjft/|()1{}[]?-_+~<>i!lI;:,"^. ', round(1 + max(0, min(66, v * 67))), 1) || CASE WHEN col=88 THEN X'0A' ELSE '' END, '') FROM res;

Рекурсивные запросы

Вот стандартный способ получить таблицу, содержащую числа от 0 до 89: 

WITH RECURSIVE numbers AS (
  SELECT 0 AS n
  UNION ALL
  SELECT n+1
    FROM numbers
    WHERE n<89
) ...

  • Рекурсивные запросы работают только в конструкции WITH. Обратите внимание, что имя, даваемое таблице, используется в ее определении.
  • SELECT 0 as n – это строка, с которой начинается рекурсивный запрос.
  • UNION ALL означает, что все строки, получаемые в результате, конкатенируются в одну таблицу без дополнительных проверок. Если написать просто UNION, будут удалены все дубликаты.
  • SELECT n+1 FROM numbers WHERE n<80. Важный нюанс здесь состоит в том, что таблица numbers всегда содержит одну строку с предыдущим числом. В какой-то момент условие в WHERE обрежет и ее и выполнение запроса прекратится. Только после этого, все предыдущие состояния таблицы будут соединены операцией UNION ALL.

Извлекаем квадратный корень

Мы будем использовать метод Герона (вавилонский метод) вычисления корня. Допустим, мы хотим вычислить $sqrt{S}$. Мы строим ряд $x_0, x_1, ldots$ по следующей формуле:

$x_{n+1}=frac{x_n + frac{S}{x_n}}{2}$

Логика метода очень простая: $sqrt{S}$ всегда лежит между $x$ и $frac{S}{x}$ для любого числа $x$. Поэтому естественно взять середину отрезка между этими числами как приближение.

Геометрически это можно изобразить так:

Трехмерный движок внутри запроса SQL - 8

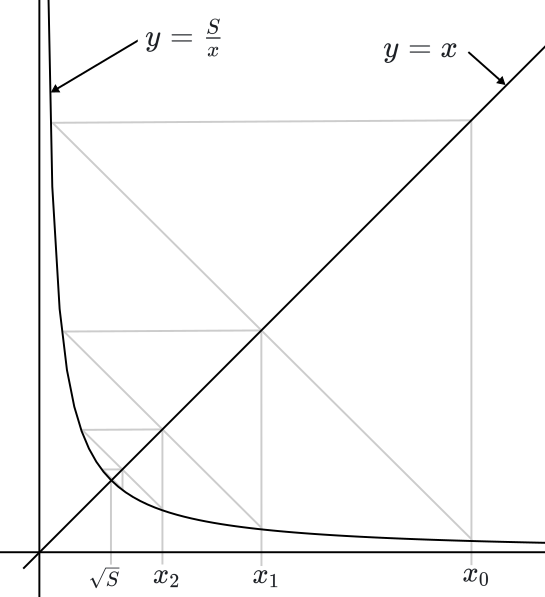
Каждое следующее значение все лучше приближает корень, за один шаг погрешность уменьшается как минимум в два раза.

Начальное значение $x_0$ может быть любым положительным числом, например 1. В игре Quake для этого использовалась магическая константа 0x5f3759df (точнее, она использовалась для инвертированного квадратного корня, тем не менее аналогичный метод может быть придуман и для обычного корня), но, к сожалению, в SQL нет доступа к двоичному представлению чисел с плавающей запятой.

В этой статье корень нужен в двух местах:

  • при нормировании векторов, выходящих из камеры: ray marching сильно зависит от расстояний, а для того, чтобы их откладывать, нужен вектор длины 1.
  • при вычислении расстояния до границы сферы, которая вырезается из квадрата.

В первом случае значения находятся в узком диапазоне $[0.7, 1.5]$ и начальное приближение 1 идеально подходит. Во втором случае, собрав статистику по вызовам, получил среднее значение $0.28$, которое было взято в качестве начального.

Оказалось, что при правильном начальном значении, достаточно одной итерации! То есть в нашем случае корень приближается линейной функцией:

$sqrt_1(x)=frac{1 + x}{2}$

$sqrt_2(x)=frac{0.28 + frac{x}{0.28}}{2}=0.14 + 1.78 x$

Вычисляем лучи из камеры

Задача первых четырех таблиц — каждому «пикселю» сопоставить трехмерный вектор длины 1, выходящий из камеры и проходящий через соответствующую точку экрана.

Сначала необходимо получить таблицу с нужной структурой, то есть с ячейками, для которых указаны номер строки и номер столбца. Для этого берется декартово произведение набора чисел от 0 до 89 и из него вырезаются пустые строки и столбцы:

...
pixels AS (
  SELECT rows.n as row, cols.n as col
  FROM numbers as rows
    CROSS JOIN numbers as cols
  WHERE rows.n >= 5 AND rows.n < 38 AND cols.n >= 10 AND cols.n < 89
),
...

Далее мы находим ненормированные вектора. В общем виде у них длинная формула из тригонометрических функций. Чтобы не усложнять запрос, я зафиксировал камеру и предрассчитал коэффициенты:

...
rawRays AS (
  SELECT
    row, col,
    -0.9049 + col * 0.0065 + row * 0.0057 as x,
    -0.1487 + row * -0.0171 as y,
    0.6713 + col * 0.0045 + row * -0.0081 as z
  FROM pixels
),
...

После этого мы должны посчитать (приблизительные) длины этих векторов по формуле $sqrt_1$:

...
norms AS (
  SELECT
    row, col, x, y, z,
    (1 + x * x + y * y + z * z) / 2.0 AS n
  FROM rawRays
),
...

Осталось разделить координаты векторов на их длину для получения векторов длины 1:

...
rays AS (SELECT row, col, x / n AS x, y / n AS y, z / n AS z FROM norms),
...

Итерации ray marching

Здесь используется чуть более сложная конструкция с рекурсивными запросами, содержащая JOIN. Мы хотим произвести 15 итераций алгоритма ray marching для каждого пикселя. Если при рекурсивном вычислении таблицы numbers каждый раз таблица содержала по одной строке, которые потом объединялись, здесь промежуточные таблицы содержат по 81 x 29 строк и вычисляются 15 раз.

Вся трехмерная геометрия содержится в формуле

$SDFbegin{pmatrix}x\ y \ zend{pmatrix}=maxleft(|x| - 0.3, |y| - 0.3, |z| - 0.3, -left(sqrt_2(x^2 + y^2 + z^2) - 0.42right)right)$

  • функция $max$ означает пересечение
  • $|x| - 0.3, |y| - 0.3, |z| - 0.3$ задают три пары полуплоскостей, образующих куб со стороной $0.3 cdot 2$
  • $-left(sqrt_2(x^2 + y^2 + z^2) - 0.42right)$ — наружная часть сферы радиуса $0.42$. Радиус взят больше видимого, чтобы компенсировать неточность приближения квадратного корня.

Далее нам надо просто вычислить последовательность $0=v_0, v_1, v_2 ldots, v_{15}$ для каждого пикселя по формуле:

$v_{n+1}=v_n + SDFleft( begin{pmatrix}camX\camY\camZend{pmatrix} + v_n begin{pmatrix}x\y\zend{pmatrix} right)$

где $x, y, z$ — координаты нормированного вектора. Так как координаты камеры повторяются несколько раз, я округлил их до одного десятичного знака.

...
iters AS (
  SELECT
    row, col,
    0 as it,
    0 as v
  FROM rays
  UNION ALL
  SELECT
    rays.row,
    rays.col,
    it + 1 AS it,
    v + MAX(
      ABS(0.7+v*x) - 0.3,
      ABS(0.7+v*y) - 0.3,
      ABS(-1.1+v*z) - 0.3,
      -(
        (0.7+v*x) * (0.7+v*x) + (0.7+v*y) * (0.7+v*y) + (-1.1+v*z) * (-1.1+v*z)
      ) * 1.78 + 0.28
    ) AS v
  FROM iters
    JOIN rays
      ON rays.row = iters.row AND rays.col = iters.col
  WHERE it < 15
),
...

Получаем интенсивности «пикселей»

Здесь используется та же формула, что и в Excel, которая аппроксимирует компоненту diffuse из затенения по Фонгу:

$intensity=maxleft(0, minleft(1, frac{v_{15} - v_{14}}{v_{14} - v_{13}}right)right) $

Чтобы ее вычислить, необходимо предварительно сделать таблицу с тремя последними итерациями ray marching:

...
lastIters AS (
  SELECT
    it0.row,
    it0.col,
    it0.v AS v0,
    it1.v AS v1,
    it2.v AS v2
  FROM iters as it0
    JOIN iters AS it1
      ON it0.col = it1.col AND it0.row = it1.row
    JOIN iters AS it2
     ON it0.col = it2.col AND it0.row = it2.row
  WHERE it0.it = 15 AND it1.it = 14 AND it2.it = 13
),
...

И, собственно, сама формула (операции $max$ и $min$ будут применены в финальном запросе):

...
res AS (SELECT row, col, (v0 - v1) / (v1 - v2) as v FROM lastIters)
...

Генерируем «ascii-арт»

...
SELECT group_concat(
  substr(
    '$@B%8&WM#*oahkbdpqwmZO0QLCJUYXzcvunxrjft/|()1{}[]?-_+~<>i!lI;:,"^. ',
    round(1 + max(0, min(66, v * 67))),
    1
  ) ||
  CASE
    WHEN col=88 THEN X'0A'
    ELSE ''
  END, 
'') FROM res;

Задача финального запроса состоит в том, чтобы конвертировать таблицу с интенсивностями пикселей в одну ascii-строку. На вход он получает только таблицу res, содержащую колонки col и v.

  • group_concat(s, delim) – агрегирующая функция, конкатенирующая выражение s для всех строк, используя строку delim в качестве разделителя.
  • CASE WHEN cond1 THEN val1 WHEN cond2 THEN val2 ... ELSE valN END – условная конструкция, аналог тернарного оператора.
  • X'0A' – символ переноса строки, который вставляется перед первым символом каждой строки.
  • || – оператор конкатенации строк.
  • substr(s, start, count) – функция, возвращающая count символов строки s, начиная с символа с номером start. Индексация символов идет с единицы.
  • '$@B%8&WM#*oahkbdpqwmZO0QLCJUYXzcvunxrjft/|()1{}[]?-_+~<>i!lI;:,"^. ' – строка, содержащая «градиент» от «черного» ($) к «белому» (пробел) в ascii-символах. Взято с сайта http://paulbourke.net/dataformats/asciiart/.
  • round(1 + max(0, min(66, v * 67))) – преобразуем вещественные числа из интервала $[0, 1]$ в целое число в интервале $[1, 67]$ чтобы взять символ с соответствующим номером.

Автор: pallada92

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js