- PVSM.RU - https://www.pvsm.ru -

Что нужно знать при написании алгоритмов на .NET

  1. Нотация О большое для оценки сложности алгоритмов

  2. Структуры данных и их применение в алгоритмах

  3. Некоторые рекомендации для разработки на .NET

При написании алгоритмов нужно учитывать их масштабируемость. Для этих целей используется понятие «О большое», представленное Паулем Бахманном в 1894 году для того, чтобы приблизительно оценивать, как время выполнения алгоритма будет расти при увеличении размеров входных данных.

Пусть f(n) — время выполнения алгоритма, а g(n)  - временная сложность, которая проверяется для алгоритма. Тогда f(n)=O(g(n)), если существует константа k (k > 0) и n0, такие, что f(n) <= kg(n) для всех n, начиная с некоторого n0 (n > n0).

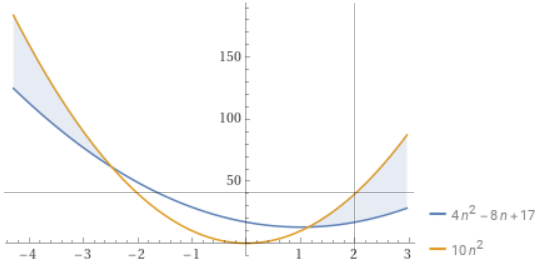
4n2-8n+17=O(n2)

4n2-8n+17=O(n2)

Пример.

Пусть f(n)=4n2-8n+17

тогда f(n)=O(n2), поскольку

4n2-8n+17 <= 10n2 при n>2

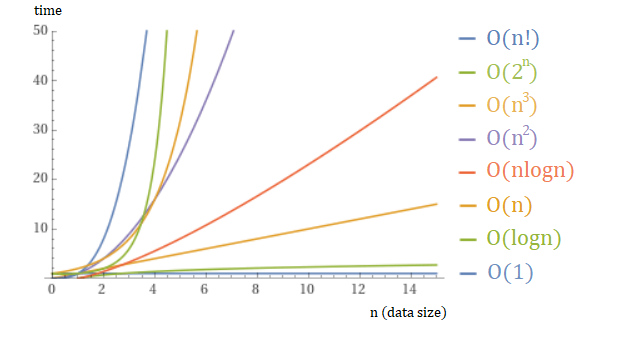
Говоря о сложности алгоритмов, часто рассматривается наихудшее время работы алгоритма, и для его описания используются следующие О нотации: 

O(1) - константная сложность - время выполнения такого алгоритма не зависит от длины исходных данных 

O(n) - линейная сложность - время выполнения такого алгоритма, прямо пропорционально длине обрабатываемых исходных данных, т.е. при увеличении размера n в 10 раз, время работы алгоритма возрастет также в 10 раз 

O(n2) - квадратичная сложность - время пропорциональное квадрату длины входных данных, т.е. при увеличении размера n в 10 раз, время работы алгоритма возрастет в 102=100 раз.

O(logn) - логарифмическая сложность - время будет расти меньше, в сравнении с линейной сложностью, но быстрее, чем у константной, например, при увеличении размера n в 10 раз, время работы алгоритма возрастет в log210 = 3.32 раза.  

O(nlogn) - линейно-логарифмическая сложность - время будет расти быстрее, чем у O(n), но медленнее, чем у O(n2). К примеру, при увеличении размера n в 10 раз, время работы алгоритма возрастет в 10log210 = 10*3.32 = 33.2 раза.

Характер роста времени в зависимости от n: самое лучшее время у O(1), O(logn), самое худшее y O(n!)

Характер роста времени в зависимости от n: самое лучшее время у O(1), O(logn), самое худшее y O(n!)

Критерии, по которым определяется сложность алгоритмов:

  • Если содержится цикл с n итерациями, то его сложность оценивается как O(n).

  • Если внутри одного цикла с n1 итерациями (внешний цикл) содержится цикл с n2 операциями (внутренний цикл), то сложность этих циклов оценивается как O(n1 * n2).

  • Если вызывается функция f(n), а затем g(n), то сложность составляет O(f(n) + g(n)).

  • Расчет сложности блока if: O(IF) = O(cond(n)) + max[O(b1(n)), O(b2(n))], где cond(n) - функция вычисления условия, O(b1(n)) - сложность вычисления блока при срабатывании условия, O(b2(n)) - сложность блока при не срабатывании условия.

Примеры алгоритмов с константной сложностью

  • Доступ к элементу массива по его индексу. 

  • Стек на базе массива: операции pop, push, size, peek. 

  • Доступ к элементу хэш-таблицы. 

Примеры алгоритмов с линейной сложностью

  • Подсчет суммы значений элементов массива, т.к. содержится один цикл с n итерациями, на каждой итерации выполняется доступ к элементу массива за O(1) и суммирование переменной за O(1), поэтому f(n) = O(n) * O(1) * O(1) = O(n) 

  • Поиск элемента в массиве (линейный поиск). 

  • Обход двоичного дерева.

Примеры алгоритмов с квадратичной сложностью

  • Суммирование значений элементов двумерного массива (вложенный цикл).

  • Сортировка методом пузырька.

Примеры алгоритмов с логарифмической сложностью

Часто в эту категорию попадают алгоритмы, созданные по стратегии “разделяй и властвуй”, например, двоичный поиск: на каждой итерации пространство поиска сокращается вдвое, что означает, что итераций будет кратно меньше, чем n.

Бинарный поиск запускается только на отсортированных данных.

Примеры алгоритмов с линейно-логарифмической сложностью

Часто в эту категорию попадают алгоритмы, где данные разделяются на несколько более мелких частей, каждая из частей обрабатывается функцией с логарифмической сложностью, а затем все обработанные части данных собираются воедино с помощью линейной операции (в цикле).

  • Сортировка слиянием: выполняется n итераций, на каждой из которых выполняется операция mergeSort, сложность которой - O(logn), т.е. mergeSort выполнится n раз. Стоит отметить, что для этого алгоритма требуется дополнительная память на n элементов (сложность по памяти O(n)).

  • Быстрая сортировка.

Примеры алгоритмов с экспоненциальной сложностью

Расчет чисел Фибоначчи при помощи рекурсии - каждый вызов функции Фибоначчи приводит к двум новым рекурсивным вызовам.

Примеры алгоритмов с факториальной сложностью

Задача коммивояжёра (TSP). Полный перебор (brute force).

Структуры данных и их применение в алгоритмах

Массивы - упорядоченный набор n элементов одного типа, хранящихся в непрерывном блоке памяти.  

+Быстрый доступ к элементам по индексу.

-Добавление/удаление элементов сопряжено с перевыделением памяти и копированием элементов в новый массив, что составляет сложность O(n), т.к. элементы копируются в цикле.

Списки - упорядоченный набор элементов одного типа, каждый элемент хранит ссылку на следующий элемент (элементы могут храниться в разных участках памяти). 

+Быстрое добавление/удаление элементов.

-Доступ к элементам сопровождается обходом по списку, следовательно сложность операции составляет O(n) в худшем случае.

При добавлении элемента в середину списка, нужно в цикле пройти по элементам до опорного, а затем обновить ссылки элементов списка: опорный ссылается на добавляемый, добавляемый ссылается на следующий за опорным.

Хеш-таблицы хранят неупорядоченные пары ключ-значение. Для доступа к значению вычисляется хеш-функция от ключа. Получающееся хеш-значение играет роль индекса в массиве, по которому извлекается значение.

+Добавление, удаление, поиск элемента в среднем выполняются за O(1).

-При достижении определенного коэффициента заполнения необходимо осуществлять перестройку индекса хеш-таблицы: создать новый массив увеличенного размера и заново добавлять в него все пары, что составляет сложность O(N).

Словари или dictionaries хранят неупорядоченные пары ключ-значение, где тип ключей должен быть хешируемым, а значения ключей - уникальными. 

+Быстрый доступ и удаление за O(1).

-Добавление элементов и поиск по значению может составлять O(n).

Стек - организован по принципу LIFO на основе массива или списка. 

+Операции добавления элемента в стек (push), удаления элемента (pop), чтения (peek) выполняются за O(1).

Очередь - организована по принципу FIFO на основе массива или списка. 

+Операции добавления элемента в очередь (enqueue), удаления элемента (dequeue), чтения из начала (front) и конца (rear) очереди выполняются за O(1).

-Если стек или очередь реализованы на базе массива, то добавление элементов может в худшем случае составлять O(n), что связано с перераспределением памяти. 

Деревья - наиболее распространены двоичные деревья, используемые для хранения иерархических данных или же упорядоченных.  

+Вставка, добавление и поиск в среднем за O(logn), в худшем - O(n).

Некоторые рекомендации для разработки на .NET

Список в .NET реализован как динамический массив, что обеспечивает быстрый доступ к его элементам по индексам: List<T> [1] содержит свойства Count [2], характеризующее число элементов списка и размер массива Capacity. [3] При количестве элементов, превышающем Capacity, массив пересоздается с увеличенным Capacity и с копированием элементов (O(n)). Capacity всегда берется с запасом, начиная с 4 и увеличивается в 2 раза (при достижении размера 2Гб будет ошибка переполнения). По такому же принципу реализован и StringBuilder [4], HashSet<T> [5] и Dictionary<TKey,TValue> [6]. Класс LinkedList<T> [7] представляет собой двухсвязный список.

Свойство Count имеет вычислительную сложность O(1).

Типы Array и List предоставляют метод Sort [8], реализованный на основе гибридного алгоритма сортировки Introsort - интроспективная сортировка (предложен Дэвидом Мюссером в 1997г), в котором сочетаются Быстрая сортировка, сортировка кучей и вставками, что гарантирует сложность O(nlogn) для худшего случая.

Типы SortedSet<T> [9] и SortedDictionary<TKey,TValue> [10] построены на основе красно-черных деревьев, а тип SortedList<TKey,TValue> [11] построен на основе двух массивов, в одном из которых хранятся ключи, а в другом - значения, отсортированные по ключу. Для хранения упорядоченных пар ключ-значение можно выбрать SortedList или SortedDictionary:

Операция 

SortedList 

SortedDictionary

Доступ по ключу

Чтение - O(logn), Запись по существующему ключу - O(logn) 

Доступ по целочисленному индексу

Свойства Keys и Values с возвращаемым типом IList<T> [12]

Не поддерживается 

Добавление элемента

O(logn) если порядок не нарушается, O(n) - если нужна переcортировка или перераспределение памяти 

O(logn)

Удаление элемента

O(n)

O(logn)

Расход памяти 

Меньше 

Больше 

При работе с non-generic коллекциями с элементами типа Object, требуется выполнять приведение типов (упаковка/boxing типов-значений в object), что чревато ошибками и снижением производительности. Предпочитайте им generic типы:

Non-generic тип 

Предпочтительный generic тип 

ArrayList [13] 

List<T> [14] 

CaseInsensitiveComparer [15] 

StringComparer.OrdinalIgnoreCase [16] 

CaseInsensitiveHashCodeProvider [17] 

StringComparer.OrdinalIgnoreCase [16] 

CollectionBase [18] 

Collection<T> [19] 

NameObjectCollectionBase [20] 

OrderedDictionary<TKey,TValue> [21]

Comparer [22] 

Comparer<T> [23] 

DictionaryBase [24]

Dictionary<TKey, TValue> [25], KeyedCollection<TKey, TItem> [26] 

DictionaryEntry [27] 

KeyValuePair<TKey, TValue> [28] 

Hashtable [29] 

Dictionary<TKey, TValue> [25] 

Queue [30] 

Queue<T> [31] 

ReadOnlyCollectionBase [32] 

ReadOnlyCollection<T> [33] 

SortedList [34] 

SortedList<TKey, TValue> [35] 

Stack [36] 

Stack<T> [37] 

Если коллекция нужна только для перебора ее элементов в foreach (только для чтения), то используйте типы из System.Collections.IEnumerable. Т.к. эти типы также queryable types, то к ним можно применять фильтрацию, группировку, сортировку с LINQ.

Для хранения пар ключ-значение используйте: 

Хранение неоднородных элементов: List<Object>, OrderedDictionary.

Хранение набора уникальных элементов: HashSet<T> [43], SortedSet<T> [9].

Быстрый поиск и извлечение данных:

Для хранения коллекции строк: StringCollection [46], StringDictionary [47].

При доступе к данным из нескольких потоков берите типы из System.Collections.Concurrent.

Везде, где только возможно, предпочитайте использовать иммутабельные типы данных, например из System.Collections.Immutable - эти типы также потокобезопасны.

Разница в производительности операций mutable/immutable типов:

Mutable 

Amortized

Worst Case 

Complexity immutable 

Stack<T>.Push 

O(1) 

O(n) 

O(1) 

Queue<T>.Enqueue 

O(1) 

O(n) 

O(1) 

List<T>.Add 

O(1) 

O(n) 

O(log n) 

List<T>.Item[Int32] 

O(1) 

O(1) 

O(log n) 

List<T>.Enumerator 

O(n) 

O(n) 

O(n) 

HashSet<T>.Add, lookup 

O(1) 

O(n) 

O(log n) 

SortedSet<T>.Add 

O(log n) 

O(n) 

O(log n) 

Dictionary<T>.Add 

O(1) 

O(n) 

O(log n) 

Dictionary<T> lookup 

O(1) 

O(n) 

O(log n) 

SortedDictionary<T>.Add 

O(log n) 

O(n log n) 

O(log n) 

Тип ImmutableList<T> [48] использует двоичное дерево для хранения элементов, что замедляет доступ по индексу.

А какие методы и структуры данных Вы предпочитаете использовать в решении задач? Какие трудности возникали при неправильном выборе структуры данных или алгоритма?

Автор: Alex9889

Источник [49]

Сайт-источник PVSM.RU: https://www.pvsm.ru

Путь до страницы источника: https://www.pvsm.ru/struktury-danny-h/404186

Ссылки в тексте:

[1] List<T>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.list-1?view=net-9.0

[2] Count: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.list-1.count?view=net-9.0

[3] Capacity.: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.list-1.capacity?view=net-9.0

[4] StringBuilder: https://learn.microsoft.com/en-us/dotnet/api/system.text.stringbuilder?view=net-8.0

[5] HashSet<T>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.hashset-1?view=net-9.

[6] Dictionary<TKey,TValue>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.dictionary-2?view=net-9.0

[7] LinkedList<T>: https://learn.microsoft.com/ru-ru/dotnet/api/system.collections.generic.linkedlist-1?view=net-8.0

[8] Sort: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.list-1.sort?view=net-9.0

[9] SortedSet<T>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.sortedset-1?view=net-9.0

[10] SortedDictionary<TKey,TValue>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.sorteddictionary-2?view=net-9.0

[11] SortedList<TKey,TValue>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.sortedlist-2?view=net-9.0

[12] IList<T>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.ilist?view=net-9.0

[13] ArrayList: https://docs.microsoft.com/dotnet/api/system.collections.arraylist

[14] List<T>: https://docs.microsoft.com/dotnet/api/system.collections.generic.list-1

[15] CaseInsensitiveComparer: https://docs.microsoft.com/dotnet/api/system.collections.caseinsensitivecomparer

[16] StringComparer.OrdinalIgnoreCase: https://docs.microsoft.com/dotnet/api/system.stringcomparer.ordinalignorecase

[17] CaseInsensitiveHashCodeProvider: https://docs.microsoft.com/dotnet/api/system.collections.caseinsensitivehashcodeprovider

[18] CollectionBase: https://docs.microsoft.com/dotnet/api/system.collections.collectionbase

[19] Collection<T>: https://docs.microsoft.com/dotnet/api/system.collections.objectmodel.collection-1

[20] NameObjectCollectionBase: https://learn.microsoft.com/en-us/dotnet/api/system.collections.specialized.nameobjectcollectionbase

[21] OrderedDictionary<TKey,TValue>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.ordereddictionary-2?view=net-9.0

[22] Comparer: https://docs.microsoft.com/dotnet/api/system.collections.comparer

[23] Comparer<T>: https://docs.microsoft.com/dotnet/api/system.collections.generic.comparer-1

[24] DictionaryBase: https://docs.microsoft.com/dotnet/api/system.collections.dictionarybase

[25] Dictionary<TKey, TValue>: https://docs.microsoft.com/dotnet/api/system.collections.generic.dictionary-2

[26] KeyedCollection<TKey, TItem>: https://docs.microsoft.com/dotnet/api/system.collections.objectmodel.keyedcollection-2

[27] DictionaryEntry: https://docs.microsoft.com/dotnet/api/system.collections.dictionaryentry

[28] KeyValuePair<TKey, TValue>: https://docs.microsoft.com/dotnet/api/system.collections.generic.keyvaluepair-2

[29] Hashtable: https://docs.microsoft.com/dotnet/api/system.collections.hashtable

[30] Queue: https://docs.microsoft.com/dotnet/api/system.collections.queue

[31] Queue<T>: https://docs.microsoft.com/dotnet/api/system.collections.generic.queue-1

[32] ReadOnlyCollectionBase: https://docs.microsoft.com/dotnet/api/system.collections.readonlycollectionbase

[33] ReadOnlyCollection<T>: https://docs.microsoft.com/dotnet/api/system.collections.objectmodel.readonlycollection-1

[34] SortedList: https://docs.microsoft.com/dotnet/api/system.collections.sortedlist

[35] SortedList<TKey, TValue>: https://docs.microsoft.com/dotnet/api/system.collections.generic.sortedlist-2

[36] Stack: https://docs.microsoft.com/dotnet/api/system.collections.stack

[37] Stack<T>: https://docs.microsoft.com/dotnet/api/system.collections.generic.stack-1

[38] Dictionary<TKey,TValue>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.idictionary-2

[39] KeyedCollection<TKey,TItem>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.objectmodel.keyedcollection-2

[40] NameValueCollection: https://learn.microsoft.com/en-us/dotnet/api/system.collections.specialized.namevaluecollection

[41] SortedList<TKey,TValue>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.sortedlist-2?view=net-8.0

[42] IComparer<T>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.icomparer-1?view=net-8.0

[43] HashSet<T>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.hashset-1?view=net-9.0

[44] ListDictionary: https://learn.microsoft.com/en-us/dotnet/api/system.collections.specialized.listdictionary

[45] SortedDictionary<TKey,TValue>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.sorteddictionary-2

[46] StringCollection: https://learn.microsoft.com/en-us/dotnet/api/system.collections.specialized.stringcollection

[47] StringDictionary: https://learn.microsoft.com/en-us/dotnet/api/system.collections.specialized.stringdictionary

[48] ImmutableList<T>: https://learn.microsoft.com/en-us/dotnet/api/system.collections.immutable.immutablelist-1?view=net-8.0

[49] Источник: https://habr.com/ru/articles/863950/?utm_source=habrahabr&utm_medium=rss&utm_campaign=863950