Алгоритм Краскала — это жадный алгоритм, который используется для нахождения минимального остовного дерева (MST) в связном, взвешенном и неориентированном графе. В контексте генерации лабиринтов он применяется для создания структуры, где каждая ячейка соединена с другими без циклов и недостижимых областей. В результате получается так называемый "идеальный лабиринт", в котором из любой точки можно попасть в любую другую по единственному пути.
Постановка задачи:
Необходимо разработать алгоритм генерации лабиринта, который удовлетворяет следующим условиям:
-
Лабиринт не содержит циклов;
-
Каждая область лабиринта достижима из любой другой;
-
Между каждой парой точек существует ровно один путь.
Как работает алгоритм:
Любой алгоритм построения MST сводится к проверке, создаёт ли добавление ребра цикл. Для этого применяется структура данных Union-Find. Этот алгоритм позволяет эффективно отслеживать, какие вершины принадлежат одному множеству, и объединять их без образования циклов.
Алгоритм Краскала выполняется следующим образом:
-
Все возможные соединения между ячейками лабиринта заносятся в список и получают случайные веса.
-
Все рёбра упорядочиваются по весу в порядке неубывания.
-
Построение остовного дерева:
-
Выбирается ребро с наименьшим весом;
-
Проверяется, соединяет ли оно две разные компоненты связности (с помощью Union-Find);
-
Если ребро не создаёт цикл, оно добавляется в MST.
-
-
Повторение. Шаги продолжаются, пока не будет добавлено (V - 1) рёбер, где V — количество вершин графа.
Разбор примера по шагам:
Как же работает этот алгоритм наглядно? Пусть у нас есть взвешенный, связный, неориентированный граф, состоящий из 6 вершин. Запишем его ребра в отсортированном порядке:
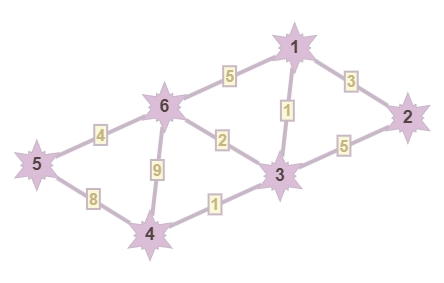
1 <—> 3 вес 1
3 <—> 4 вес 1
3 <—> 6 вес 2
1 <—> 2 вес 3
5 <—> 6 вес 4
1 <—> 6 вес 5
2 <—> 3 вес 5
4 <—> 5 вес 8
4 <—> 6 вес 9
Теперь по списку добавляем ребра в наше дерево, разумеется, избегая образования циклов.
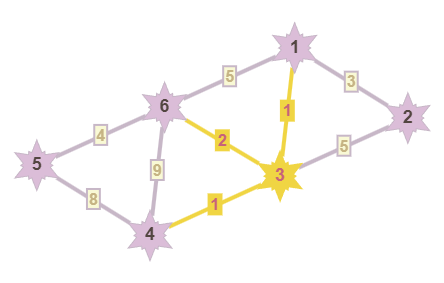
Добавляем вершины дальше, можем заметить, что, например, ребро между вершинами 1 и 6 добавить мы не можем, так как тогда образуется цикл. Тогда, после второго обхода получим следующий результат:
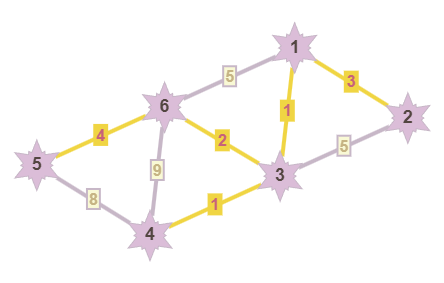
По итогу у нас образовывается следующий подграф. Мы соединили все вершины ребрами с минимально-возможными весами, а значит, наше минимальное остовное дерево готово! :)
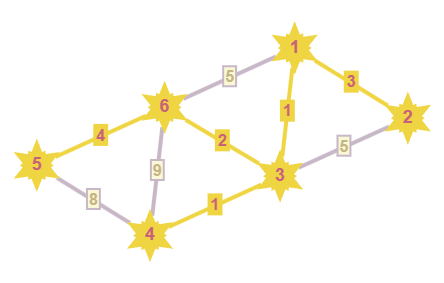
Тогда суммарный вес искомого MST будет сумма весов всех выделенных ребер, а именно 11
Реализация:
1. Базовое представление лабиринта.
Для реализации Краскала на такой задаче, нужно учитывать особенности представления матрицы. При использовании алгоритма Краскала для генерации лабиринта обычно работают с базовой сеткой ячеек, где каждая ячейка — это потенциальное «помещение», а между ними располагаются стены. Исходная матрица формируется таким образом, что каждая ячейка базовой сетки располагается по координатам 2 × rows_cells + 1, 2 × cols_cells+ 1. Между ними располагаются потенциальные проходы, а оставшиеся позиции заполняются стенами.
2. Построение остовного дерева.
Остовное дерево — это подграф, соединяющий все вершины графа без циклов и с минимальным числом ребер. Алгоритм Краскала начинается с формирования списка всех ребер, соединяющих соседние ячейки базовой сетки. Каждому ребру присваивается случайный вес, после чего список сортируется. Union-Find — это структура данных для эффективного отслеживания объединений и принадлежности элементов к различным множествам. С помощью этой структуры происходит последовательное объединение ячеек, принадлежащих разным компонентам связности, при этом добавление ребра допускается только если оно не создает цикл.
3. Преобразование базовой сетки в итоговый лабиринт.
После построения остовного дерева создаётся матрица конечного лабиринта размером:
result_rows = 2⋅rows_cells − 1, result_cols = 2⋅cols_cells − 1.
При этом:
-
На позициях 2 × rows_cells, 2 × cols_cells копируются ячейки базовой сетки.
-
Между ячейками (на позициях с нечетными и четными индексами) устанавливаются значения, отражающие наличие проходов.
-
Особый случай — лабиринт из одной ячейки — корректируется путем удаления лишней стены.
4. Корректировка размеров.
При вводе, например, 4 × 4, базовая логика приводит к лабиринту 3 × 3. Чтобы итоговый лабиринт соответствовал требованиям, используются вспомогательные функции:
-
add_extra_row: добавляет в конец матрицы строку, заполненную стенами, и открывает проходы в каждом втором столбце.
-
add_extra_col: аналогично добавляет столбец, корректируя позиции так, чтобы сохранить правило расположения ячеек и стен.
Преимущества и недостатки
Преимущества
-
Генерация «идеального» лабиринта (perfect maze):
Факт: Алгоритм Краскала строит остовное дерево (spanning tree) заданного графа. В контексте лабиринта вершинами являются ячейки, а рёбра – потенциальные проходы.
Доказательство: Остовное дерево по определению не содержит циклов и соединяет все вершины графа. Это означает, что между любыми двумя ячейками существует ровно один уникальный путь. Таким образом, генерируемый лабиринт не имеет избыточных проходов, а его структура однозначна (нет альтернативных маршрутов), что часто называют «идеальным» лабиринтом.
-
Случайность и равномерность распределения проходов:
Факт: При генерации лабиринта Краскала присваивает случайные веса ребрам, что делает сгенерированные алгоритмы визуально красивыми и равномерными.
Доказательство: Поскольку все возможные ребра сортируются по случайным весам, вероятность выбрать любое конкретное ребро одинакова. Таким образом, результирующее остовное дерево (а значит и лабиринт) получается равновероятным выбором из всех возможных остовных деревьев данного графа. Это математически гарантирует, что лабиринт будет случайным и непредсказуемым, что является желаемым свойством для игр и головоломок.
Недостатки алгоритма Краскала
-
Ограниченность в контроле над структурными характеристиками лабиринта:
Факт: Алгоритм Краскала генерирует равновероятное остовное дерево, иногда это может стать минусом.
Доказательство: Математически, если рассматривать все возможные остовные деревья на заданном графе, каждое генерируется с одинаковой вероятностью. Это означает, что нет простого способа сместить распределение в сторону лабиринтов с длинными коридорами, большим количеством тупиков или иных желаемых особенностей без изменения базового алгоритма. В некоторых приложениях требуется именно такой контроль над «характером» лабиринта, а равновероятное распределение остовных деревьев может оказаться неудачным.
теперь будем приводить сравнение с еще двумя алгоритмами, подходящими для этой задачи Recursive Backtracker и Hunt and Kill
2. Временная сложность
Алгоритм Краскала хуже Recursive Backtracker и Hunt and Kill в плане скорости работы, так как сортировка рёбер даёт дополнительный логарифмический множитель.
-
Краскал: O(E LogE), где E — количество ребер (примерно O(RC log(RC)) для лабиринта R×C). Сортировка рёбер доминирует во времени работы.
-
Recursive Backtracker: O(RC) — за один проход посещает все ячейки.
-
Hunt and Kill: O(RC) — тоже за один проход.
3. Использование памяти
Краскал не так эффективен по памяти, как Hunt and Kill, но примерно равен Recursive Backtracker в худшем случае.
-
Краскал: хранит список рёбер и массив для Union-Find, что требует O(RC) памяти.
-
Recursive Backtracker: использует стек вызовов рекурсии, в худшем случае O(RC), но в среднем меньше.
-
Hunt and Kill: O(1), так как работает без стека и дополнительных структур.
4. Сложность реализации
Recursive Backtracker проще всего для понимания и реализации, Hunt and Kill немного сложнее, а Краскал — самый сложный.
-
Краскал: требует работы с рёбрами, сортировки, структуры Union-Find. Реализовать сложнее.
-
Recursive Backtracker: проще, так как это DFS с рекурсией.
-
Hunt and Kill: тоже довольно простой, но менее интуитивный.
Доп. Материал
Здесь вы можете посмотреть примеры сгенерированных лабиринтов (с их путями) размерами от 1 × 1 до 25 × 25. Там же описано построение пути в лабиринте - на случай экспериментов.
Источники:
-
“Алгоритм Краскала - Алгоритмика.” 2017. Algorithmica.org. 2017. https://ru.algorithmica.org/cs/spanning-trees/kruskal/.
-
Batu Senturk. 2024. “Kruskal’s Algorithm: The Most Visually Satisfying Maze Generation.” Medium. July 18, 2024. https://medium.com/@batbat.senturk/kruskals-algorithm-the-most-visually-satisfying-maze-generation-c5c565844a4e.
-
Buck, Jamis. 2011. “Buckblog: Maze Generation: Kruskal’s Algorithm.” Weblog.jamisbuck.org. January 3, 2011. https://weblog.jamisbuck.org/2011/1/3/maze-generation-kruskal-s-algorithm.
-
GeeksforGeeks. 2012. “Kruskal’s Minimum Spanning Tree Algorithm.” GeeksforGeeks. October 30, 2012. https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/.
-
Rasul Yunusov. 2021. “Алгоритм Краскала, Прима для нахождения минимального остовного дерева.” Хабр. Habr. July 24, 2021. https://habr.com/ru/articles/569444/.
-
2020. Washington.edu. 2020. https://courses.cs.washington.edu/courses/cse326/07su/prj2/kruskal.html.
Автор: leenakwa





