Всем привет! Меня зовут Константин Некрасов, я работаю дата-сайентистом в Газпромбанке. Хочу рассказать про инструмент, который серьезно упростил мою повседневную работу с данными, и поделиться им.
Если вы когда-нибудь занимались машинным обучением, то знаете — перед тем как строить модель, нужно как следует изучить свои данные. Этот этап называется EDA (Exploratory Data Analysis), или разведочный анализ данных (РАД). Он критически важен — именно здесь мы находим скрытые закономерности, выдвигаем первые гипотезы и понимаем, как лучше обработать данные для будущей модели.
Но EDA отнимает у дата-сайентистов кучу времени, которое можно потратить на что-то другое и не менее важное: придумать новые признаки, поэкспериментировать с разными алгоритмами или настроить гиперпараметры для более высокой точности модели.
Чтобы облегчить задачу, я разработал класс EDAProcessor, который автоматизирует ключевые этапы EDA: от базовой статистики и визуализации распределений до углубленного анализа корреляций, выбросов и временных зависимостей. Результаты анализа сохраняются в виде наглядных графиков и подробной excel-таблицы, где на разных листах представлены все важные статистические показатели и закономерности в данных.
Сразу оговорюсь — я не изобретаю здесь новых статистических методов, не претендую на научную новизну в области математической статистики, а мое решение не универсально. Каждый набор данных уникален, и полностью автоматизировать его анализ невозможно — всегда нужен опытный взгляд аналитика. Но базовые, наиболее часто используемые методы EDA этот инструмент берет на себя, ускоряя начальный этап работы с данными. Я попытался собрать в скрипт наиболее общие концепции EDA, которые используются в подавляющем большинстве случаев на первоначальной стадии разработки ML-модели.
Сам скрипт вот тут, а под капотом я расскажу, что он делает.
Что к чему
Не буду здесь дублировать код, чтобы не увеличивать объем статьи, а опишу только функционал конкретных функций класса EDAProcessor, а также покажу выводы на примере одного набора данных.
1. Функция generate_eda_summary
Предоставляет первоначальную статистику по набору данных, а именно выводит информацию по каждому столбцу: количество пропущенных строк, в том числе в процентом соотношении; тип данных; количество уникальных значений; показывает все уникальные значения в категориальных типах данных (object, category, string). Помимо прочего, дается первоначальная рекомендация по удалению столбцов:
-
"Удалить (константный столбец)": если в столбце всего одно уникальное значение (константа).
-
"Удалить (ID или уникальные значения)": если количество уникальных значений равно количеству строк (например, столбец с уникальными идентификаторами).
-
"Оставить": во всех остальных случаях.
Также под сводной таблицей выводится информация о количестве дубликатов в наборе данных по строкам и столбцам.

2. Функция plot_target_distribution
Выводит график распределения целевой переменной и сводную таблицу формата pandas DataFrame под графиком.
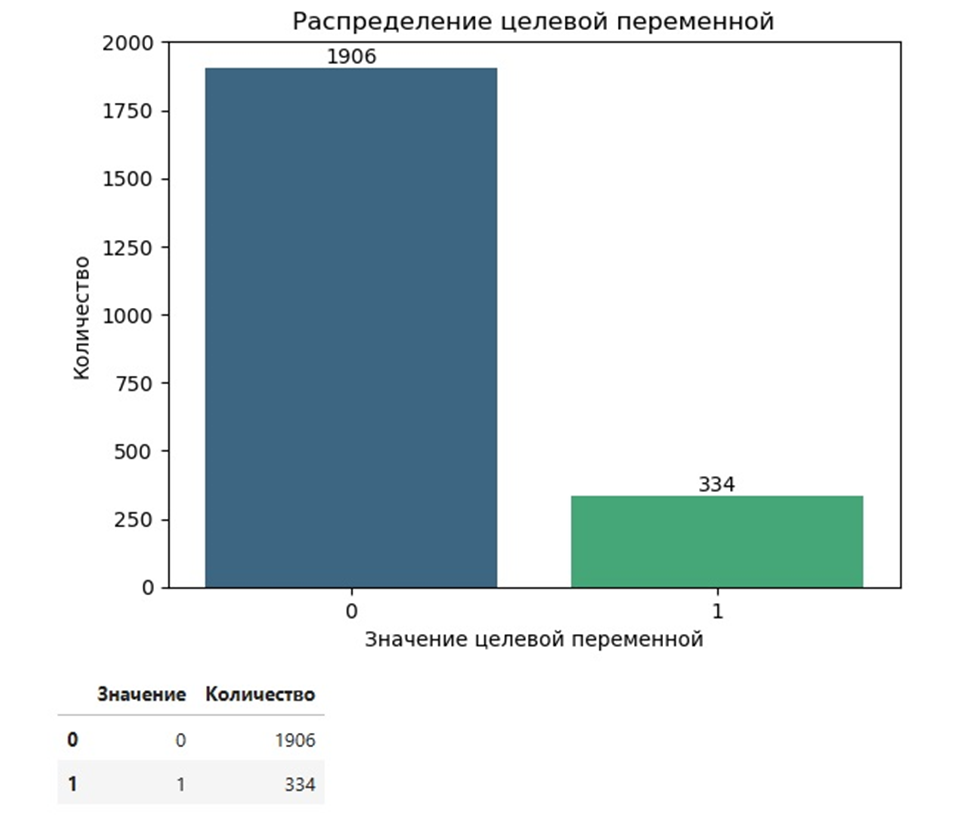
3. Функция plot_categorical_distributions
Выводит гистограммы распределения элементов для всех категориальных признаков, имеющихся в наборе данных. Также выводится и сводная таблица, отражающая информацию с графиков.
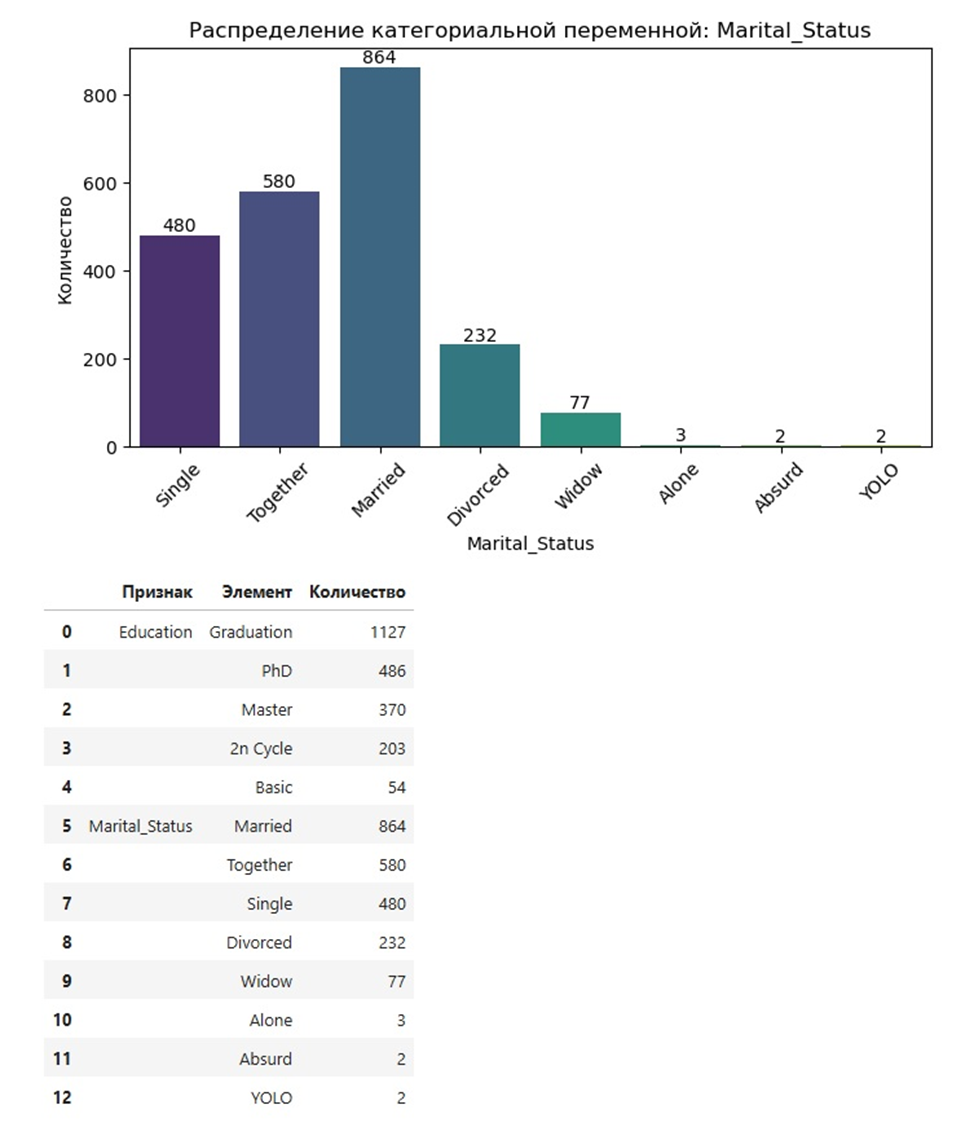
4. Функция plot_categorical_vs_target
Часто при проведении разведочного анализа данных необходимо посмотреть, как ведет себя какой-то категориальный признак по отношению к целевой переменной. Данная функция позволяет провести такое сравнение. Выводится график зависимости конкретной категориальной переменной, задаваемой разработчиком (аналитиком данных), от целевой переменной.

5. Функция plot_kde_distributions
Выполняет построение гистограмм и графиков KDE (Kernel Density Estimation) для числовых признаков в наборе данных. Она помогает визуализировать распределение данных, выявлять аномалии, выбросы и анализировать отклонения от нормального распределения.
Вкратце напомню, что KDE — это метод сглаживания данных для оценки их плотности. График KDE визуализирует, как распределены значения в выборке, и позволяет понять общую форму распределения, даже если данные не распределены нормально.
На графике KDE можно определить:
-
пики распределения, указывающие на моды (значения, которые встречаются чаще всего);
-
хвосты распределения, помогающие анализировать наличие выбросов;
-
симметричность распределения, что важно для гипотез, предполагающих нормальность данных.
Итак, на графике добавлены следующие показатели:
-
Сама гистограмма распределения числовых признаков. Она показывает частоту появления значений в интервалах. Используется для первоначального анализа распределения данных.
-
KDE-линия. Непрерывная кривая, отражающая плотность данных. Позволяет лучше оценить форму распределения, чем дискретная гистограмма.
-
Среднее значение. Показывает центр тяжести данных, но может быть смещено выбросами.
-
Медианное значение. Значение, делящее данные пополам. Устойчиво к выбросам.
-
Перцентили. 25-й и 75-й перцентили показывают границы интервала, содержащего 50% данных. 99-й перцентиль помогает определить верхний хвост распределения, где могут находиться редкие значения (выбросы).
-
Линия идеального нормального распределения. Строится поверх фактического распределения для сравнения. Идеальное нормальное распределение, добавляемое на график для сравнения с фактическими данными, позволяет визуально оценить степень отклонения реального распределения от нормального. Анализ отклонений, таких как асимметрия или длинные хвосты, помогает выдвигать гипотезы о трансформациях данных.
Например, для правосторонне асимметричных распределений может быть предложена логарифмическая трансформация, которая уменьшает разброс и приближает данные к нормальному распределению. Подобные преобразования облегчают использование методов анализа, предполагающих нормальность данных. Исходя из сказанного выше, можно сделать вывод о том, что идеальное нормальное распределение помогает подготовить данные для алгоритмов машинного обучения, которые чувствительны к отклоняющимся от нормы распределениям.
-
Пик KDE. Указывает значение с максимальной плотностью, что помогает понять, где сосредоточена большая часть данных.

Помимо графиков, функция plot_kde_distributions также возвращает сводную таблицу со всеми параметрами, отраженными на графике, а также дополнительными статистиками:
-
Эксцесс. Показывает, насколько распределение «пиковое» или «плоское».
-
Асимметрия. Указывает на перекос распределения.
-
Распределение значений. Отображается межквартильный диапазон (от 25-го до 75-го перцентиля).
-
Вывод о типе распределения (нормальное, смещенное вправо или влево).

6. Функции detect_outliers_iqr и detect_outliers_zscore
Обе направлены на то, чтобы при помощи графиков вида «ящик с усами» определить выбросы в числовых переменных набора данных.
6.1 detect_outliers_iqr
Реализует метод IQR (Interquartile Range) для поиска выбросов. По данному методу значения считаются выбросами, если выходят за границы:
где
-
Q₁ и Q₃ — это первый и третий квартиль;
-
IQR = Q₃ − Q₁.
Вывод функции представлен в виде графика «ящик с усами»:

Также под всеми графиками выводится сводная таблица с информацией о выбросах:

6.2 detect_outliers_zscore
Эта функция также служит для поиска выбросов, но реализуется через метод Z-score. Согласно данному методу, значения считаются выбросами, если их Z-score превышает заданный порог (обычно 3) и вычисляется по формуле:
где
-
X — значение;
-
μ — среднее;
-
σ — стандартное отклонение.
Для данного анализа из создается копия набора данных и удаляются пропуски. Вывод функции также представлен в виде графика «ящик с усами»:

Аналогично выводится и сводная таблица с выбросами под графиками:

Тут может возникнуть вопрос: для чего нужна реализация двух методов, если выводы одинаковые? Ответ кроется в различиях самих методов: IQR устойчив к выбросам, так как использует квартильные значения, а не среднее, в свою очередь Z-score чувствителен к выбросам, так как выбросы могут значительно сместить среднее и увеличить стандартное отклонение, уменьшая значение Z-score для самого выброса.
Z-score наиболее эффективен, если данные приближаются к нормальному распределению. Выбросы в таком случае легко определяются как значения, выходящие за пределы []. Также, если данные симметричны, Z-score может лучше обнаруживать выбросы, поскольку среднее значение μ и стандартное отклонение σ не искажаются асимметрией. Помимо прочего, метод Z-score полезен для анализа выбросов во временных рядах, особенно если ряды являются стационарными.
7. Функция analyze_categorical_cross_tabulations
Предназначена для анализа взаимосвязей между категориальными переменными в наборе данных.
Предварительно, для проведения такого анализа, функция убирает пропущенные значения в каждой паре столбцов, которые сравниваются, а также игнорирует столбцы, в которых есть форматы дат, чтобы избежать некорректной интерпретации категорий.
В итоге для каждой пары категориальных переменных создается таблица сопряженности (кросс-таблица), которая показывает частоту совместного появления значений двух переменных.
Помимо прочего, проводится анализ взаимосвязей между парами категориальных переменных. Функция проверяет, является ли связь однозначной. По результатам проверки взаимосвязи между переменными дается вывод:
-
Четкая взаимосвязь 1:1: каждой категории одной переменной соответствует только одна категория другой переменной.
-
Неоднозначные связи: одна категория может соответствовать нескольким категориям другой переменной.
Такой анализ на этапе EDA помогает выявить взаимосвязи не только между числовыми переменными, но и между категориальными. По итогу можно, например, сократить размерность данных за счет объединения переменных с четкой взаимосвязью, а также выявить избыточные или малоинформативные признаки.
Таблица сопряженности является своего рода аналогом матрицы корреляции, но для категориальных переменных. Схожесть проявляется в том, что обе таблицы помогают оценить взаимосвязь между переменными. Как матрица корреляции показывает силу и направление связи между числовыми признаками, так таблица сопряженности демонстрирует частоты совместного появления категорий для категориальных переменных. Но также следует понимать, что хоть кросс-таблица и похожа на матрицу корреляции, однако это не одно и тоже. Ключевое различие состоит в том, что матрица корреляции количественно оценивает связь с помощью коэффициентов (например, Пирсона или Спирмена), в то время как таблица сопряженности показывает только частоты, без числовой меры силы связи.
Вывод функции выглядит следующим образом:

Как правильно читать подобную таблицу и прослеживать взаимосвязи? Из вывода видно, что у нас есть два категориальных признака: Education и Marital_Status. Каждый из этих признаков содержит соответствующие категории. Мы видим, что образованные люди (Graduation) чаще всего находятся в браке (Married, частота — 433 случая) и реже одиноки (Single, 252) или просто встречаются с кем-то (Together, 286).
Подобную связь мы можем проследить и с другими категориями обоих признаков. На основании того, что одна категория может соответствовать нескольким категориям другой переменной, мы получаем вывод, что связь между категориями Education и Marital_Status носит неоднозначный характер.
8. Функция find_rare_categories
Предназначена для выявления редких категорий в категориальных переменных. Работает она следующим образом: вычисляются доли каждой категории (частоты появления относительно общего числа записей), а затем происходит сравнение полученного результата с заданным порогом (по умолчанию threshold равен 5%). Категории, доля которых меньше порога, считаются редкими.
Проведение такого анализа может быть полезно. Во-первых, для поиска аномалий в категориальных данных: редкие категории могут быть индикаторами ошибок в данных или содержать полезную информацию, требующую отдельного анализа. Во-вторых, для принятия решения о том, что делать с такими категориями. Так, например, исключение редких категорий или их объединение помогает моделям сосредоточиться на значимых признаках, улучшая обобщающую способность модели.
Функция напоминает анализ распределения частот категорий, но фокусируется на выявлении малых значений. Это особенно важно для категориальных переменных с высокой кардинальностью, где многие категории могут встречаться лишь единично.

9. Функция analyze_correlations
Предназначена для анализа корреляций между признаками в наборе данных и целевой переменной. Она позволяет оценить силу и направление связи между числовыми переменными или определить зависимость между числовыми и категориальными переменными с использованием различных статистических подходов.
Изначально функция разделяет все признаки на числовые и категориальные. Для числовых признаков корреляция с целевой переменной вычисляется тремя методами — Пирсона, Спирмена и Кендалла. Для категориальных же рассчитываются коэффициенты Крамера и phi. Все результаты вносятся в сводную таблицу, куда также добавляется классификация по шкале Чеддока.
Может возникнуть резонный вопрос, зачем выводить корреляцию с тремя коэффициентами? Ответ заключается в том, что выбор, каким именно методом анализа руководствоваться в том или ином случае, зависит от природы данных. Для лучшего понимания этого вопроса вспомним, как высчитываются и когда применяются те или иные коэффициенты.
9.1. Корреляция Пирсона
где
-
xᵢ, yᵢ — значения переменных.
-
x̄, ȳ — выборочные средние значения параметров x и y.
Корреляция Пирсона оценивает линейную зависимость между двумя переменными, принимая значения от -1 (полная отрицательная корреляция) до 1 (полная положительная корреляция). 0 в данном случае означает отсутствие линейной связи. Данный метод подходит для анализа нормально распределенных данных.
9.2. Корреляция Спирмена
где
-
— разность рангов для пары значений;
-
— количество наблюдений.
Это ранговая корреляция, оценивающая монотонность связи между переменными. Она устойчива к выбросам и не требует нормальности данных. Используется, если зависимость между переменными нелинейная, но монотонная.
9.3. Корреляция Кендалла
где
-
— количество согласованных пар (оба значения пары возрастают или убывают);
-
— количество несогласованных пар (одно значение возрастает, другое убывает);
-
— количества одинаковых значений (тайс в рангах) для каждой переменной.
9.4. Phi-коэффициент
где
-
— значение критерия chi-квадрат;
-
— общее количество наблюдений.
Phi-коэффициент измеряет силу связи между двумя переменными на основе таблицы сопряженности. Диапазон значений от 0 до 1. Чем ближе значение к 1, тем связь между переменными сильнее. Обязательными условиями для проведения такого анализа являются следующие: во-первых, анализируемые переменные должны быть измерены в дихотомической шкале, во-вторых, число сравниваемых переменных должно быть одинаковым.
9.5 Коэффициент V Cramer's
В научной литературе переводится как коэффициент Крамера-В / Крамера-У. Также можно увидеть название коэффициент фи Крамера.
где
-
— коэффициент phi;
-
— количество столбцов;
-
— количество строк.
Диапазон значений коэффициента Крамера от 0 до 1. Подходит для анализа более сложных зависимостей между переменными. Также имеет ряд обязательных условий для проведения анализа: а) переменные должны быть измерены в номинальной шкале, где количество кодировок больше двух (не дихотомические шкалы); б) число сравниваемых переменных должно быть одинаковым.
Высокие значения коэффициента Крамера или V Cramer’s могут свидетельствовать о сильной взаимосвязи между признаками, даже если линейная корреляция отсутствует.
Эти коэффициенты полезны, если распределения данных не линейны или содержат много повторяющихся значений.
Общие выводы. Корреляции Пирсона, Спирмена и Кендалла хорошо работают с непрерывными числовыми переменными. Phi и V Cramer's позволяют анализировать числовые данные в контексте их частотного распределения. Важно отметить, что в подавляющем большинстве случаев, если исходный набор данных будет размерностью более 2 х 2, коэффициент phi будет неинформативным и в соответствующей колонке сводной таблицы будут проставлены значения None. Также следует отметить, что в представленной таблице коэффициент Cramer's V будет актуален для числовых данных только в тех случаях, когда числовые данные действительно представляют собой дискретные категории (например, возраст в годах, уровни дохода, оценки от 1 до 10). В остальных случаях этот коэффициент хорошо работает лишь с категориальными данными.
Для лучшего понимания, на какие корреляционные значения обращать внимание в том или ином случае, подойдет табличное сравнение:
|
Метод |
Тип зависимости |
Требование к данным |
Когда использовать |
|
Корреляция Пирсона |
Линейная |
Нормальное распределение, без выбросов |
Для оценки прямой линейной связи между переменными. |
|
Корреляция Спирмена |
Монотонная |
Любые распределения |
Если данные содержат выбросы или связь нелинейна. |
|
Корреляция Кендалла |
Монотонная |
Маленькие выборки, одинаковые значения |
Для небольших выборок или когда важна точность ранговой зависимости. |
|
Phi-коэффициент |
Частотная (категориальная) |
Таблицы сопряженности 2 × 2 |
Для числовых данных, преобразованных в категории, или для бинарных признаков. |
|
Коэффициент V Cramer's |
Частотная (категориальная) |
Таблицы сопряженности произвольного размера |
Для оценки связи в таблицах сопряженности с несколькими категориями. |
Помимо прочего, для методов Пирсона, Спирмена и Кендалла выводится шкала Чеддока. Эта шкала используется для интерпретации силы корреляции. Она разделяет абсолютное значение коэффициента корреляции на категории:
|
Значение |
Сила связи |
|
< 0.1 |
Очень слабая |
|
0.1–0.3 |
Слабая |
|
0.3–0.5 |
Умеренная |
|
0.5–0.7 |
Заметная |
|
0.7–0.9 |
Высокая |
|
> 0.9 |
Весьма высокая |
Вывод таблицы выглядит следующим образом:

Представленный анализ подойдет, если целевая переменная — числовая. А как быть, если она категориальная? Функция analyze_correlations работает и в таком случае. Проводится два анализа:
1. Описанный в п. 9.5 метод Cramer's V, с оговоркой, что теперь он применяется только для категориальных значений и не учитывает числовые переменные. Следует отметить, что для интерпретации связей используется шкала размера эффекта (effect size).
|
Значение |
Сила связи |
|
≤ 0.2 |
Слабая |
|
0.2–0.6 |
Умеренная |
|
> 0.6 |
Сильная |
Тут приведу дополнительно только пример вывода такого анализа:
2. ANOVA. На этом методе остановимся немного подробней.
ANOVA (Analysis of Variance) — метод статистического анализа, который проверяет, есть ли значимые различия между средними значениями групп, определенных по категориальной переменной.
где
-
— межгрупповая дисперсия (Mean Square Between);
-
— внутригрупповая дисперсия (Mean Square Within).
ANOVA используется для оценки зависимости между числовыми признаками и категориальной целевой переменной.
Статистические показатели, которые используются в ANOVA, — это F-статистика и p-value.
F-статистика (F-значение) измеряет различия между группами, то есть отношение между средними значениями в группах и дисперсией внутри групп. Если F-значение большое, то это указывает на статистически значимые различия между группами.
p-value (вероятность) — это вероятность того, что различия между группами были случайными и не связаны с фактором, который изучается. Если p-value меньше выбранного уровня значимости (в нашем случае <0.05), то можно отбросить нулевую гипотезу и утверждать, что между группами есть статистически значимые различия.
Пример вывода теста ANOVA:

10. Функция analyze_phik_correlations
Функция analyze_phik_correlations предназначена для анализа взаимосвязей между признаками с использованием Phik-коэффициента. Этот метод является универсальным и подходит для любых типов данных: числовых, категориальных или их сочетания. Phik-коэффициент позволяет определить силу зависимости между переменными вне зависимости от их природы.
Phik-коэффициент — это мера зависимости, основанная на таблицах сопряженности и позволяющая оценить силу связи между признаками. Этот коэффициент считается расширением хи-квадрат-статистики и масштабируется в диапазоне от 0 до 1:
-
0 — отсутствие зависимости;
-
1 — полная зависимость.
В функции явно задается порог значимости threshold, который по умолчанию равен 0.5. Пары признаков с Phik-значением выше порога threshold включаются в итоговую таблицу.
Также в итоговой таблице выводится категория связи согласно следующей градации:
|
Значение Phik |
Сила связи |
|
0 <= Phik <= 0.2 |
Слабая |
|
0.2 < Phik <= 0.4 |
Умеренная |
|
0.4 < Phik <= 0.6 |
Заметная |
|
0.8 < Phik <= 0.8 |
Высокая |
|
Phik > 0.8 |
Очень высокая |
Так как по умолчанию у меня стоит threshold = 0.5, то в примере не будет значений ниже чем заметная.

11. Функция analyze_datetime_attributes
Предназначена для анализа временных атрибутов из столбца с временными метками. Она позволяет выделить ключевые характеристики временных данных (год, месяц, день, час) и визуализировать их распределения, включая наложение кривой плотности KDE и кривой идеального нормального распределения. Функция возвращает сводные таблицы частот для каждого временного атрибута.
Сначала столбец с датой, если он имеет тип, отличный от datetime, преобразовывается в этот формат для извлечения атрибутов времени. Затем для каждого временного атрибута (час, день, месяц, год) строится гистограмма с наложением кривой плотности KDE, а также отображается кривая нормального распределения для оценки отклонений.

Данные графики служат для проверки следующих гипотез:
-
Равномерность распределения: если распределение временных атрибутов близко к нормальному, это указывает на равномерность событий. При этом отклонения могут свидетельствовать о сезонности или трендах.
-
Сезонность данных: например, можно проверить, в какие дни или месяцы есть больше всего наблюдений. Это может помочь с выдвижением дальнейших гипотез, которые пригодятся при разработке ML-модели.
-
Наличие аномалий в данных: если распределение далеко от нормального или имеет пики в неожиданных местах, это может указывать на аномалии.
Помимо прочего, для удобства, как и в предыдущих случаях, для каждого атрибута времени создается таблица частот, показывающая количество записей для каждого значения. Также на графике присутствуют линии среднего и медианного значения для более подробного анализа.

12. Функция decompose_time_series
Выполняет декомпозицию временного ряда. Это помогает глубже понять структуру временного ряда и выявить скрытые закономерности, такие как долгосрочные тренды, циклические паттерны и случайные шумы.
Данные столбца типа datetime сортируются по дате для последовательного анализа. Временные метки устанавливаются в качестве индекса. После этого происходит декомпозиция временного ряда. Для этого используется метод STL (Seasonal-Trend decomposition using Loess) для разделения временного ряда на три компоненты:
-
тренд (Trend): долгосрочные изменения во временном ряду;
-
сезонность (Seasonal): повторяющиеся циклы (например, месяцы или недели);
-
остатки (Residual): случайные шумы и отклонения.
STL (Seasonal-Trend decomposition using Loess) — это метод декомпозиции временных рядов, который позволяет выделить тренд, сезонность и остатки. Этот метод: не требует равномерного распределения данных, подходит для данных с произвольным временным периодом (например, 12 месяцев, 7 дней), устойчив к выбросам.
В данном случае интересной представляется формула нахождения остатков, которая рассчитывается следующим образом:
где
-
Yₜ — исходное значение временного ряда;
-
Tₜ — тренд;
-
Sₜ — сезонность.
Подобный анализ нужен для проверки следующих гипотез:
-
Долгосрочная ли динамика: устойчив ли рост или спад? Например, растут ли продажи за последние 5 лет?
-
Сезонность: есть ли месяцы или дни, в которые значения резко увеличиваются или уменьшаются?
-
Наличие аномалий: выявление периодов, которые не вписываются в общий тренд или сезонность.

Помимо представленных графиков, также выводится и сводная таблица со статистиками декомпозиции.

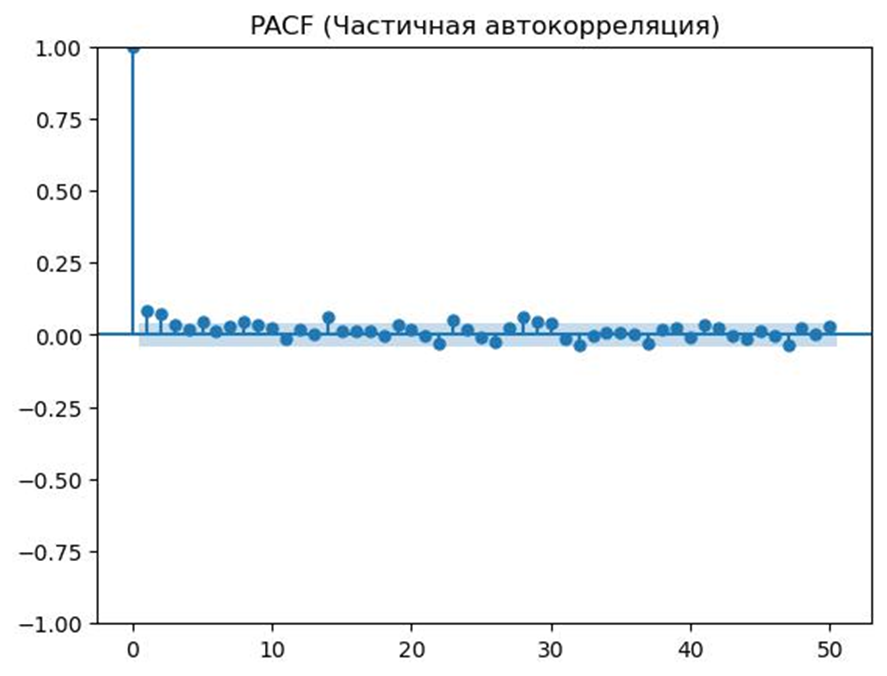
13. Функция plot_autocorrelations
Выполняет анализ временного ряда с использованием автокорреляции (ACF) и частичной автокорреляции (PACF). Она визуализирует эти зависимости на графиках и возвращает таблицу со значениями автокорреляции и частичной автокорреляции для заданного числа лагов.
13.1 ACF (Autocorrelation Function)
Измеряет степень зависимости текущего значения временного ряда от его прошлых значений на разных лагах. Она вычисляется как коэффициент корреляции между значениями временного ряда, смещенными на определенное число лагов.
где
-
k — лаг (смещение);
-
N — общее число наблюдений;
-
Yₜ — значение временного ряда в момент времени t;
-
Ȳ — среднее значение временного ряда.
Высокие значения ACF на малых лагах (lag = 1,2) указывают на сильную зависимость. В свою очередь быстрое снижение ACF с увеличением лага может свидетельствовать об отсутствии долгосрочной автокорреляции.
13.2 PACF (Partial Autocorrelation Function)
Измеряет прямую зависимость текущего значения временного ряда от его значений на определенном лаге k, исключая влияние промежуточных лагов.
Формула PACF для лагов базируется на методе регрессионного анализа. Чтобы рассчитать частичную автокорреляцию для лага k, используется следующая процедура:
1. Построить линейную регрессию в зависимости от всех предыдущих лагов
2. Рассчитать коэффициент корреляции между Yₜ и Y₍ₜ₋ₖ₎, исключив влияние промежуточных лагов.
PACF помогает определить порядок модели временного ряда, например для ARIMA. Резкое снижение значений PACF после определенного лага (lag = p) может указывать на количество лагов для модели AR (autoregressive).
Различия между двумя подходами заключается в том, что ACF оценивает полное влияние значений на всех лагах, включая косвенные зависимости, в то время как PACF оценивает прямое влияние значений на конкретном лаге, устраняя влияние промежуточных значений.
В итоге функция возвращает графики автокорреляции ACF / частичной автокорреляции PACF:


Также выводится и сводная таблица с расчетом ACF и PACF:

14. Функция check_stationarity
Используется для проверки стационарности временного ряда с помощью теста Дики-Фуллера (Augmented Dickey-Fuller Test, ADF). Стационарность — это ключевая характеристика временного ряда, которая указывает на то, что статистические свойства (например, среднее, дисперсия) ряда не изменяются со временем.
Тест Дики-Фуллера (ADF) — это статистический тест, который проверяет наличие единичного корня в процессе временного ряда. Наличие единичного корня означает, что ряд не является стационарным.
Гипотезы теста:
-
Нулевая гипотеза (H₀): временной ряд не стационарен (имеет единичный корень).
-
Альтернативная гипотеза (H₁): временной ряд стационарен.
Тест основывается на следующей модели регрессии:
где
-
ΔYₜ — разность временного ряда в момент времени t (ΔYₜ = Yₜ - Y₍ₜ₋₁₎);
-
β₀ — свободный член (константа);
-
β₁t — линейный тренд (время t);
-
αY₍ₜ₋₁₎ — лаговое значение временного ряда Y₍ₜ₋₁₎;
-
γ∑₍ᵢ₌₁ᵖ₎ ΔY₍ₜ₋ᵢ₎ — сумма лаговых разностей ΔY₍ₜ₋ᵢ₎ = Y₍ₜ₋ᵢ₎ - Y₍ₜ₋ᵢ₋₁₎ с коэффициентом γ;
-
εₜ — ошибка (остаток) в момент времени t;
-
p — количество лагов.
ADF-тест проверяет, равен ли коэффициент α нулю. Если α < 0, то ряд стационарен.
Интерпретация результатов может быть представлена следующим образом:
ADF Statistic. Если значение статистики меньше критического значения (например, ADF Statistic < Critical Value (5%)), то ряд считается стационарным.
p-value:
-
Если p < 0.05, то отклоняется нулевая гипотеза, и ряд считается стационарным.
-
Если p ≥ 0.05, то нулевая гипотеза не отклоняется, и ряд считается нестационарным.
Критические значения используются для сравнения со статистикой теста ADF. Уровни 1%, 5% и 10% задают различные уровни значимости.
Результат стационарности выводится в виде логического значения (True/False).

15. Функция plot_seasonality_heatmap
Визуализирует сезонные изменения временного ряда в виде тепловой карты. Она помогает обнаружить паттерны и зависимости, которые повторяются с определенной периодичностью, например по месяцам, дням недели или часам суток. Результаты представлены в виде тепловой карты и таблицы для средних значений.


Такой анализ позволяет:
-
выявлять сезонные паттерны и аномалии в данных;
-
визуализировать временные зависимости в удобной форме;
-
проверять гипотезы, связанные с повторяющимися событиями.
16. Функция plot_time_series_with_table
Предназначена для визуализации временного ряда и возврата данных, использованных для построения графика, в табличном формате. Эта функция также сочетает удобство графического анализа с возможностью работы с табличными данными.

График позволяет выявить:
-
Тренды. Если график демонстрирует монотонное увеличение или уменьшение значений, это может свидетельствовать о наличии тренда.
-
Сезонные колебания. Регулярные всплески или падения значений могут указывать на сезонные зависимости.
-
Аномалии. Резкие отклонения значений (вверх или вниз) могут свидетельствовать об аномальных событиях.
Результаты для более детального анализа также выводятся в табличном значении:
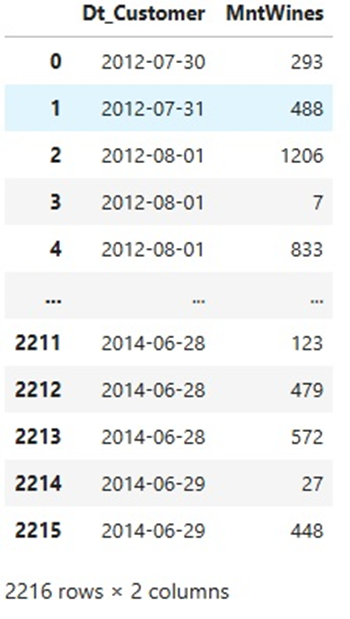
17. Функция save_all_summaries_to_excel
Используется для сохранения множества сводных таблиц в один excel-файл, где каждая таблица размещается на отдельном листе. Это удобно для хранения результатов анализа данных в структурированном и доступном формате.

Именно благодаря этой функции становится возможным создавать автоматические отчеты в табличном формате с использованием различных статистических тестов.
Итог
Еще раз стоит обратить внимание на то, что подобная автоматизация не дает полной информации о данных, и, разумеется, в каждом отдельном случае могут понадобиться дополнительные исследования в зависимости от задачи и природы данных. Однако такой скрипт упрощает работу в части общего анализа. Бесспорен и тот факт, что частично подобный инструментарий уже реализован в виде отдельных модулей, используемых аналитиками данных в работе библиотек. При этом итоговый отчет, формируемый разработанным скриптом, с подробной аналитикой данных в процессе EDA-анализа, у таких библиотек отсутствует.
Уважаемые коллеги, буду рад вашим комментариям и фидбэку по данному скрипту. Также, если у кого-то возникнут мысли о том, как можно его обогатить, пожалуйста, пишите свои предложения.
Еще раз напомню, что с полной версией скрипта, в том числе и с его использованием, можно ознакомиться в репозитории: https://github.com/NeKonnnn/Exploratory_Data_Analysis.
Автор: NeKonn











