Привет! Это заметка о небольшом хобби-проекте, которым я занимался в свободное время. Я расскажу, как с помощью несложных алгоритмов превращать карты глубины от depth-сенсоров в забавный вид контента — динамические 3D сцены (их ещё называют 4D video, volumetric capture или free-viewpoint video). Моя любимая часть в этой работе — алгоритм триангуляции Делоне, который позволяет превращать разреженные облака точек в плотную полигональную сетку. Приглашаю всех, кому интересно почитать про алгоритмы, самописные велосипеды на C++11, и, конечно же, посмотреть на трёхмерных котиков.
Для затравки: вот что получается при использовании RealSense R200: skfb.ly/6snzt (подождите несколько секунд для загрузки текстур, а затем используйте мышку, чтобы поворачивать сцену). Под катом есть ещё!
Обладатели лимитированных тарифов, будьте осторожны. В статье много разных изображений и иллюстраций.
Дисклеймер: в этой статье не будет ни слова про искусственный интеллект, блокчейн или гравитационные волны. Это просто небольшая игрушка, которую я написал в основном для того, чтобы освежить C++ и OpenGL. Всё, ожидания сформированы, поехали!
Какое-то время назад мне в руки попал девайс с 3D сенсором, а именно планшет Google Tango Development Kit с технологией structured light. Естественно, у меня чесались руки запрограммировать что-нибудь для этого интересного устройства.
Как раз примерно в то же время я впервые познакомился с новым видом контента — 4D видео. Под “4D видео” я понимаю трёхмерные сцены, которые эволюционируют во времени нетривиальным образом, т.е. их поведение нельзя описать простой моделью, вроде скелетной анимации или блендшейпов. Короче, что-то похожее на вот это:
Такой контент показался мне очень интересным; я решил поэкспериментировать с ним немного и написать своё приложение для генерации 4D роликов. Конечно, у меня нет студии и ресурсов как у Microsoft Research, да и сенсор всего один, поэтому результаты будут намного скромнее. Но это не остановит любителя программировать, правильно? О том, что у меня получилось, я и расскажу в этой статье.
Большая часть аудитории, несомненно, знакома с 3D сенсорами. Самый массовый девайс в этой категории — всем известный Kinect, очень успешный продукт компании Microsoft. Однако несмотря на относительную распространённость, для многих людей depth-сенсоры остаются чем-то диковинным. Нам же будет полезно разобраться с принципом их работы прежде чем начинать писать приложения.
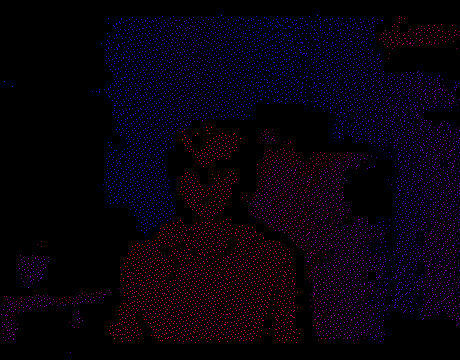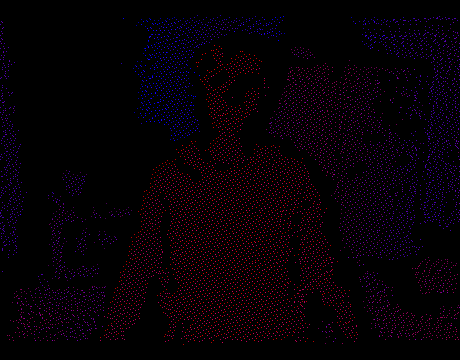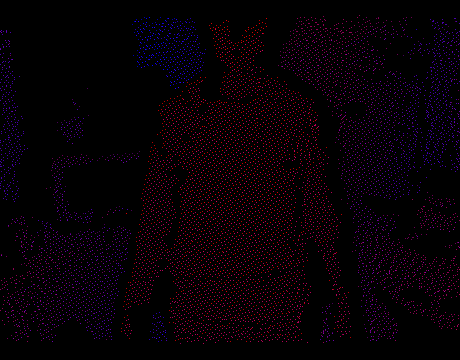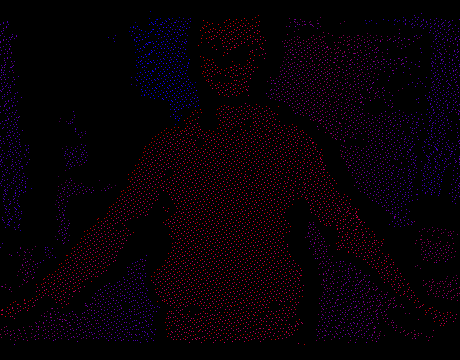
С Google Tango и другими structured light устройствами всё относительно понятно. Встроенный в девайс инфракрасный прожектор проецирует на сцену нерегулярный паттерн из световых точек, примерно как на этой картинке:
Затем специальный софт превращает искажения этого паттерна на изображении с ИК-камеры (вызванные разнообразной формой объектов) в серию 3D измерений. Для каждого светового пятнышка на снимке алгоритм восстанавливает пространственные координаты, и на выходе мы получаем 3D облако точек. Внутри, конечно же, всё устроено намного интереснее, но это тема для целой отдельной статьи.
Что ж, нужно проверить как это работает на практике! За пару вечеров на коленке было написано простое приложение-граббер для Tango-планшета на Android, и вот у меня есть мой самый первый dataset.
Хотя первая версия граббера была очень сырой, главное было достигнуто: координаты точек записались в бинарный файл. На скриншоте показано как выглядит облако точек с одного кадра в программе Meshlab.
Ок, облака точек это уже интересно. Однако point cloud — весьма “разреженное” представление сцены, ведь разрешение современных structured light сенсоров довольно низкое (обычно в районе 100x100 точек, плюс-минус). Да и в целом, в мире компьютерной графики гораздо привычнее другое представление 3D объектов и сцен, а именно полигональные сетки, или меши.
Если подумать, задача получения меша по облаку точек с одной 3D камеры довольно проста, значительно проще, чем произвольный meshing в 3D. Для этого нам не нужны никакие марширующие кубы или реконструкция Пуассона. Вспомним, что точки были получены с помощью одной единственной IR-камеры и естественным образом проецируются обратно на фокальную плоскость:
Теперь мы можем решать задачу в 2D, забыв на время про Z-координату. Чтобы получить полигоны нужно всего лишь триангулировать множество точек на плоскости. Как только это сделано, мы проецируем вершины обратно в 3D используя внутренние параметры IR-камеры и известную в каждой точке глубину. Триангуляция будет диктовать связность между вершинами, т.е. каждый треугольник мы интерпретируем как грань меша. Таким образом на каждом кадре получится настоящая 3D модель сцены, которую можно отрендерить в OpenGL, открыть в Blender и т.п.
Итак, всё что осталось сделать — найти триангуляцию для точек на каждом кадре. Есть масса способов триангулировать множество точек в 2D, и по сути любая триангуляция даст нам какой-то меш. Но ровно один способ является оптимальным для построения полигональной сетки — триангуляция Делоне.
Эту интересную конструкцию уже не раз упоминали на Хабре, но я всё таки напишу пару слов. Все из нас видели диаграммы Вороного. Диаграмма Вороного для множества точек S это такое разбиение плоскости на ячейки, где каждая ячейка содержит все точки наиболее близкие к одному из элементов S.
А триангуляция Делоне это такая триангуляция, которая в смысле теории графов двойственна диаграмме Вороного:
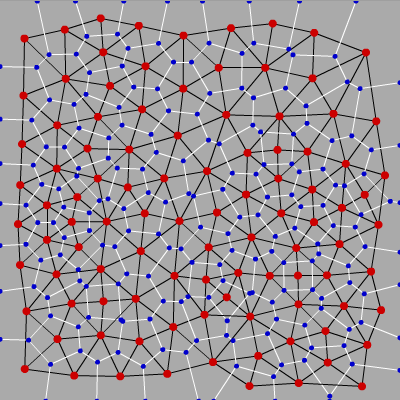
Триангуляции Делоне обладают множеством замечательных свойств, но нам особенно интересны вот эти два:
- Описанная около любого из треугольников окружность не содержит в себе точек множества, кроме вершин самого треугольника.
- Триангуляция Делоне максимизирует минимальный угол среди всех углов всех треугольников, тем самым избегаются вырожденные и «тонкие» треугольники.
Свойство #2 достаточно интуитивно следует из #1. Действительно, чтобы описанные окружности не содержали посторонних точек, они должны быть по возможности небольшими, а радиус окружности для “тонких” треугольников (близких к вырожденным) наоборот очень велик. Таким образом триангуляция Делоне максимизирует количество “хороших” треугольников, далёких от вырожденных. А значит и наш меш должен выглядеть хорошо.
Сказано — сделано, пишем триангуляцию Делоне. Есть множество известных алгоритмов, самые простые начинаются где-то с 
. Но раз люди научились считать эти триангуляции за 
, мы просто не можем быть медленнее!
Как и во многих других подобных задачах, алгоритм строится по принципу “разделяй и властвуй”. Будем сортировать точки по координатам x и y, а затем рекурсивно генерировать и объединять триангуляции пока не получится один большой граф. Достаточно показать вот этот кусочек кода, чтобы стало понятно, что здесь происходит:
const uint16_t numRight = numPoints / 2, numLeft = numPoints - numRight;
EdgeIdx lle; // CCW convex hull edge starting at the leftmost vertex of left triangulation
EdgeIdx lre; // CW convex hull edge starting at the rightmost vertex of left triangulation
EdgeIdx rle; // CCW convex hull edge starting at the leftmost vertex of right triangulation
EdgeIdx rre; // CW convex hull edge starting at the rightmost vertex of right triangulation
triangulateSubset(lIdx + numLeft, numRight, rle, rre);
triangulateSubset(lIdx, numLeft, lle, lre);
mergeTriangulations(lle, lre, rle, rre, le, re);
В принципе всё, можно расходиться.
На самом деле нет, потому что самое интересное начинается в функции mergeTriangulations. Действительно, если мы разделили наше множество пополам достаточное число раз, мы остались с кусочками по две или три точки, с которыми мы как-нибудь разберёмся:
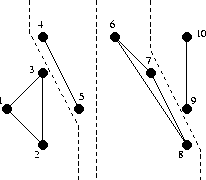
А что потом?
На самом деле тоже ничего сложного. В каждом листе рекурсии мы уже получили валидное решение подзадачи. Осталось подняться вверх по стеку, по пути сливая левое и правое разбиение в единое целое. Но делать это нужно аккуратно, т.к. далеко не каждый способ слияния даст нам на выходе триангуляцию Делоне.
Алгоритм Гибаса и Столфи предлагает весьма элегантное решение этой проблемы. Идея в том, чтобы воспользоваться свойством #1, которое я упомянул выше, но обо всём по порядку.
Сперва немного обозначений; давайте назовём левую триангуляцию L, а правую R. Тогда рёбра, принадлежащие левой триангуляции будем называть LL, т.к. они начинаются и заканчиваются в точках левого подмножества. Ребра правой триангуляции назовём RR, а рёбра, которые мы будем добавлять между левой и правой половиной — LR, точно как на иллюстрации:
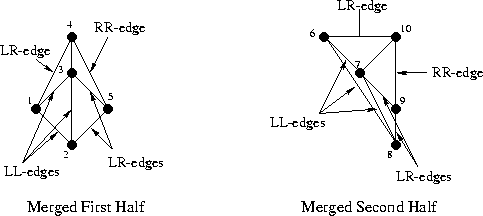
Как видно, здесь мы уже “помёржили” стартовые треугольнички и рёбра в триангуляции аж из целых четырёх треугольников. Все рёбра, которые присутствовали на предыдущем шаге отмечены как LL или RR, а все новые рёбра — LR. Процесс слияния на этом шаге не показан, так как он весьма тривиален, и не позволит показать особенности алгоритма. А вот на следующем шаге будет интереснее, давайте его и рассмотрим. Вот так выглядит наша задача перед началом слияния:
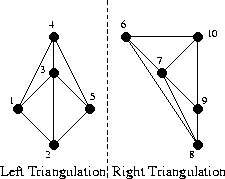
Заметим, что “внешние” рёбра и в левой и в правой половине (такие как 1-2, 2-5, 5-4, 6-8) образуют выпуклые оболочки своего подмножества точек. Понятно, что такие рёбра всегда принадлежат триангуляции Делоне, да и вообще любой триангуляции. Заметим также, что при слиянии двух непересекающихся разбиений нам всегда нужно будет добавить ровно два новых ребра, чтобы достроить выпуклую оболочку объединённого множества (грубо говоря, “накрыть” точки новыми рёбрами сверху и снизу). Отлично, у нас уже есть два новых LR-ребра! Выберем одно из них, нижнее, и назовём его “базой” (в коде — base).
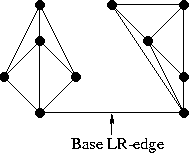
Теперь мы должны добавить следующее ребро, смежное с base, при этом один из его концов совпадает с концом base, а другим концом является точка либо из L, либо из R. Собственно, нам и нужно решить какой из двух вариантов является правильным. Начнём с правой стороны. Первым кандидатом будет точка, связанная с правым концом base RR-ребром с наименьшим углом по часовой стрелке относительно base. Следующими по очереди кандидатами будут точки R, соединённые с правой вершиной base RR-рёбрами с увеличивающимся значением угла относительно base, как показано на иллюстрации:
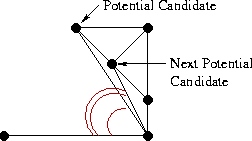
Теперь для каждого кандидата нужно проверить два условия:
- Угол между base и кандидатом не должен превышать 180 градусов (нас интересуют только те точки, что “выше” base).
- Окружность, описанная вокруг base и точки-кандидата не должна содержать в себе следующую точку-кандидат.
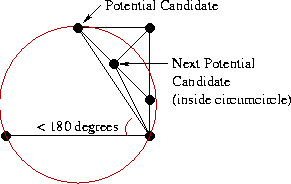
В зависимости от конфигурации вершин здесь может быть несколько вариантов:
- Нашлась точка-кандидат, которая удовлетворяет обоим критериям. Отлично, это и будет наш выбор для правой стороны.
- Если не выполняется требование #1 (угол < 180 градусов), значит мы уже достигли “верха”, и более нет необходимости выбирать точки с правой стороны. Рассматриваем только левую триангуляцию.
- Самый интересный случай — выполняется условие #1, но не #2 (см. иллюстрацию). В этом случае нам нужно удалить RR-ребро, которое соединяет base с точкой-кандидатом и повторить поиск заново.
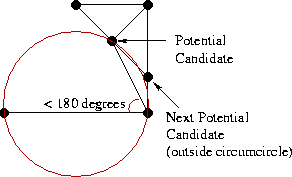
Естественно, процесс для левой половины абсолютно симметричен.
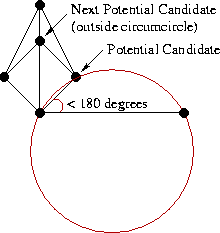
Таким образом при каждом добавлении нового LR-ребра мы выбираем точку-кандидат из левой и правой половины. Если ни там, ни там не нашлось подходящей точки, значит мы завершили слияние и нужно подниматься дальше по стеку. Если нашлась одна точка (только слева или только справа), мы добавляем LR-ребро с концом в ней. Если точки нашлись с обеих сторон, мы повторяем тест с окружностью: строим описанную окружность вокруг base и точки-кандидата из L и R. Выбираем ту точку, чья окружность не содержит кандидата из противоположной половины. Факт: такая точка всегда будет единственной, если только четыре вершины не образуют прямоугольник. В этом случае можно выбрать любой из вариантов.
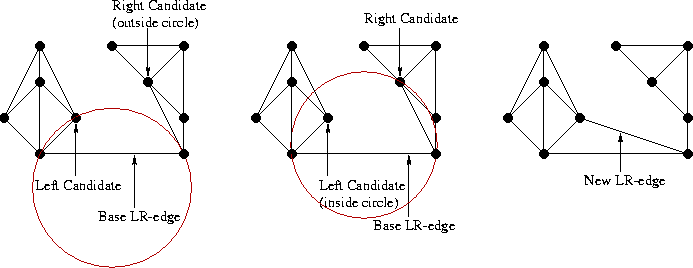
В данном примере мы выбираем кандидата из L, потому что соответствующая окружность не содержит точку-кандидата из R.
После того как новое LR-ребро добавлено, оно становится новой “базой” (base). Повторяем обновление base пока не достигнем верхнего ребра выпуклой оболочки:
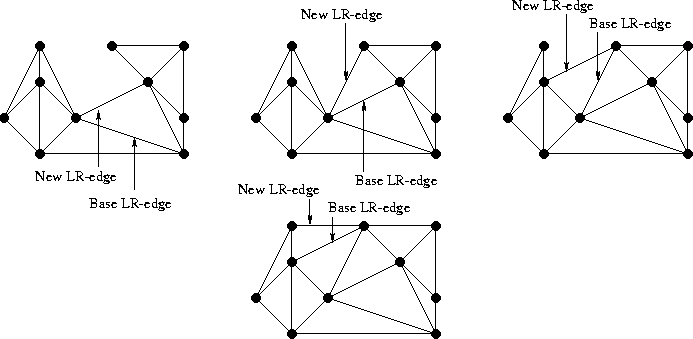
Оказывается, если наш алгоритм будет аккуратно следовать описанным правилам, то после слияния левой и правой половины мы получим валидную триангуляцию Делоне для L∪R.
”Я нашёл этому поистине чудесное доказательство, но поля данной книги слишком узки для него”. На самом деле, если вам интересно, откуда взялись все утверждения, например про необходимость удаления рёбер, рекомендую исследовать работу Гибаса и Столфи, ключевые леммы под номерами 9.2, 9.3, 9.4, 8.3.
Что ж, теперь соберём всё вместе и посмотрим что получится:
Это визуализация работы алгоритма, который у меня получился. Здесь оранжевым отмечено ребро base, зелёным — LL-кандидат, синим — RR-кандидат. Красным помечены рёбра, которые не удовлетворяют критерию #2 и будут удалены.
Пока описание алгоритма ещё свежо в памяти, очень легко понять, что он действительно выполняется за 
. Действительно, мы имеем порядка 
операций слияния; даже если на каждой из них мы вынуждены будем удалить и перестроить вообще все рёбра, количество действий всё равно останется порядка 
(т.к. это триангуляция, а не произвольный граф, количество ребер линейно относительно количества точек). На самом деле, на большинстве реальных задач скорость работы лучше чем 
и близка к линейной; нужен какой-нибудь особенно больной датасет, чтобы заставить алгоритм перестраивать триангуляцию с нуля на каждой стадии слияния.
Ещё одно замечание — из полученной триангуляции легко получить и выпуклую оболочку, и диаграмму Вороного для соответствующего множества точек. Приятный бонус.
Интересно сказать пару слов про структуру данных, которую я использовал для работы с графом. Обычно графы представляют как списки или матрицы смежности, но в данной задаче нас интересует не только связность, но и некоторые геометрические свойства графа. Вот что у меня получилось:
struct TriEdge
{
uint16_t origPnt; // index of edge's origin point
EdgeIdx symEdge; // index of pair edge, with same endpoints and opposite direction
EdgeIdx nextCcwEdge; // next counterclockwise (CCW) edge around the origin
EdgeIdx prevCcwEdge; // previous CCW edge around the origin (or next CW edge)
};Это в некотором роде урезанная версия структуры, которую предлагают Гибас и Столфи. Как говорится, всё гениальное просто. Для каждого ребра мы храним точку, из которой оно “выходит” (origin), индекс его парного ребра, направленного в противоположную сторону, а также индексы следующего и предыдущего ребра “вокруг” origin-точки. По сути получается двусвязный список, но так как мы поддерживаем относительное расположение рёбер вокруг их концов, многие шаги алгоритма кодируются просто элементарно.
В некоторых других работах предлагается хранить не рёбра, а сразу треугольники. Я пробовал экспериментировать с таким вариантом, и могу сказать, что объем кода вырастает в разы, т.к. приходится вводить многочисленные костыли для особых случаев (вырожденные треугольники, точки на бесконечности и т.п.). И хотя у такого варианта есть потенциальное преимущество в плане использования памяти, я всячески рекомендую использовать двусвязные списки рёбер. Работать с ними в разы приятнее.
Я думаю с этого момента можно перестать притворяться, что кому-то интересны детали реализации алгоритма. Можно просто расслабиться и позалипать на эти замечательные анимации.
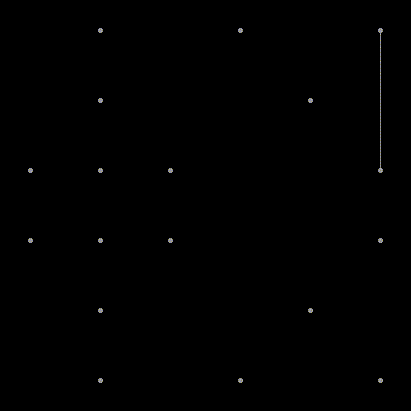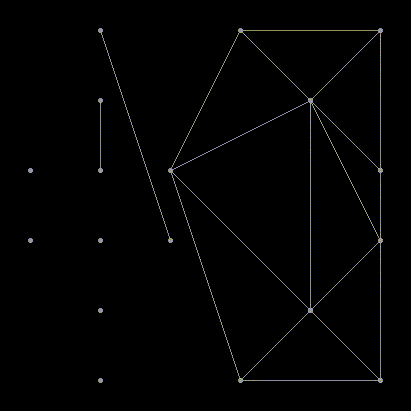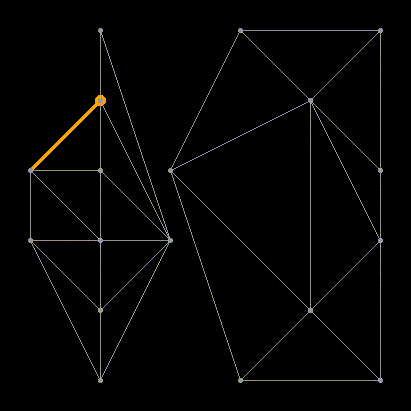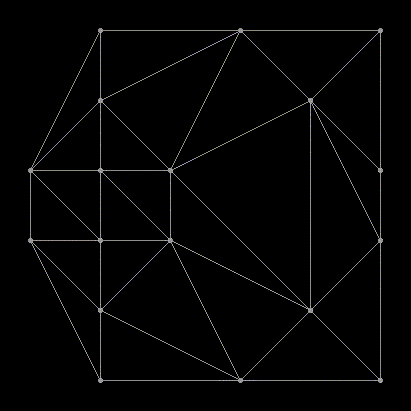
Как насчёт регулярной сетки?
Здесь точки удачно поделились на подмножества и вообще не пришлось удалять никакие рёбра. Но так бывает не всегда.
Уже интереснее. Количество точек на стороне решётки стало нечётным и из-за этого алгоритм вынужден делать довольно много исправлений. Как насчёт окружности из точек?
Интересно! Но мне больше нравится с точкой в центре:
Я думаю, к этому моменту статья содержит достаточное количество GIF-анимаций. Чтобы у читателей с ограничениями по трафику осталось хоть немного интернета после загрузки этой статьи, я залил остальные анимации на видео-хостинг.
Рекомендуется залипать в 1080p и 60fps, это оригинальное разрешение видео. Причём лучше развернуть на весь экран, иначе рёбра графа получаются алиасными.
Я осознаю, что эти видео интересны далеко не всем, но на меня они производят такой же эффект, как заставка “трубопровод” в старых версиях Windows. Оторваться сложно.
Эти анимации стали главной причиной, почему статья писалась так долго. Note to self: в следующий раз обойтись дебаггером и трейсами, делать дебажные визуализации опасно :) Если кто-то хочет посмотреть на работу алгоритма на других конфигурациях точек, пишите в комментариях, я с удовольствием сгенерирую ещё анимаций.
Развлекаться с визуализацией было весело, но пришло время вспомнить для чего изначально создавался алгоритм. Мы собирались генерировать полигональный меш из данных с depth-сенсора. Что ж, давайте возьмём облако точек с сенсора, спроецируем на плоскость камеры и запустим алгоритм триангуляции.
(Не спрашивайте меня сколько рендерился этот ролик. Бедный ffmpeg.)
Итак, отлично! Хотя на данном этапе у нас есть только граф из точек и рёбер, из него элементарным образом можно сгенерировать массив треугольников. Осталось только отфильтровать некрасивые полигоны вытянутые по Z-координате, которые возникают на границах объектов и сделать простой проигрыватель на OpenGL:
Здесь хорошо видно, что первая версия граббера была очень сырой: половина кадров не успели записаться, из-за этого картинка замирает. Короче, едва ли режиссёрский шедевр. Но это не важно — алгоритмы наконец-то ожили! Для меня это было настоящее “Прибытие поезда”!
После этого я снял ещё пару роликов, я залил их на ресурс Sketchfab в формате timeframe animation, мне кажется так будет интереснее.
Датасет #2 в WebGL
Датасет #3 в WebGL
Что ж, пайплайн заработал и стало ясно, что дальнейшее развитие ограничивают возможности железа. Действительно, планшет Tango позволяет снимать только с очень низкой частотой кадров (5 fps), а ведь основная идея была в том, чтобы запечатлеть динамический характер сцен. Есть ещё одно существенное ограничение: в Tango не синхронизированы RGB и IR камеры, то есть получение кадров происходит в разные моменты времени. Это не критично для, скажем, сканирования статических объектов, т.к. Tango SDK позволяет найти преобразование между позами RGB и IR для соседних кадров с помощью встроенного трекинга на основе высокочастотного акселерометра и fisheye камеры. Но с движущимися объектами это совершенно не помогает, и для меня отсутствие синхронизации означало, что на меш не получится натянуть текстуру.
К счастью у меня был ещё один девайс — Intel RealSense R200. Чудесным образом R200 не имеет обоих недостатков, т.к. он развивает до 60(!) fps и имеет отличную синхронизацию всех своих камер. Так что я решил написать приложение-граббер для R200 (на этот раз на C++, а не на Java) и продолжить эксперименты.
Сразу же выяснилось, что с моим пайплайном есть небольшая проблема. С увеличенным разрешением и высокой частотой съемки, которую позволяет R200, производительности уже не хватало, чтобы генерировать меш на каждом кадре в реалтайме. Профилировка показала, что узкое место — это конечно же триангуляция. Первоначальная версия была написана достаточно “расслабленно”, с динамическим выделением памяти, использованием STL и т.п. Кроме того, первая версия работала с координатами типа float, хотя в моей задаче точки всегда имеют целочисленные координаты (позиции в пикселях на картинке). Так что неудивительно, что хороший с точки зрения асимптотики алгоритм работал на моём ноутбуке до 30 миллисекунд на тестовом кадре с Tango (около 12000 точек). Потенциал для ускорения был очевиден и я увлечённо засел оптимизировать. Развивались события как-то так:
- Первым делом на алтарь скорости отправились числа с плавающей точкой. Все алгоритмы (где это возможно) перешли на целочисленные вычисления.
- Вторым на очереди было динамическое выделение памяти. Теперь вся память для алгоритма выделялась один раз, “на худший случай”, и затем переиспользовалась. Не самое эффективное решение с точки зрения потребления памяти (в духе ACM ICPC), но это дало значительное ускорение.
- На сайте проекта посвящённого численной симуляции землетрясений был найден замечательный тест на нахождение точки внутри описанной окружности треугольника:
Вот его реализация:
FORCE_INLINE bool inCircle(int x1, int y1, int x2, int y2, int x3, int y3, int px, int py) { // reduce the computational complexity by substracting the last row of the matrix // ref: https://www.cs.cmu.edu/~quake/robust.html const int p1p_x = x1 - px; const int p1p_y = y1 - py; const int p2p_x = x2 - px; const int p2p_y = y2 - py; const int p3p_x = x3 - px; const int p3p_y = y3 - py; const int64_t p1p = p1p_x * p1p_x + p1p_y * p1p_y; const int64_t p2p = p2p_x * p2p_x + p2p_y * p2p_y; const int64_t p3p = p3p_x * p3p_x + p3p_y * p3p_y; // determinant of matrix, see paper for the reference const int64_t res = p1p_x * (p2p_y * p3p - p2p * p3p_y) - p1p_y * (p2p_x * p3p - p2p * p3p_x) + p1p * (p2p_x * p3p_y - p2p_y * p3p_x); assert(std::abs(res) < std::numeric_limits<int64>::max() / 100); return res < 0; }
Эти три мероприятия дали очень значительное ускорение, с 30000+ до 6100 микросекунд на кадр. Но можно было ускорить ещё:
- Сделал некоторым небольшим функциям __forceinline, 6100 -> 5700 микросекунд, редкий случай когда компилятор сам не догадался.
- Удалил #pragma pack(push, 1) для стуктуры TriEdge. И почему я решил, что с запаковкой будет быстрее? 5700 -> 4800 микросекунд.
- Заменил std::sort для точек на самописную сортировку, похожую на radix. 4800->3700 микросекунд.
Итого получилось ускорить код почти в 10 раз, и я думаю это не предел. Кстати, я не поленился собрать код для Android, и на схожей задаче ARM процессор Tango работал около 10 миллисекунд на кадр, т.е. 100 fps! Короче, получился даже немного overkill, но если кому-то нужна очень быстрая “целочисленная” триангуляция Делоне, то добро пожаловать в репозиторий.
Теперь мои алгоритмы были готовы к R200, и вот первый датасет, который я снял:
За ним, естественно, последовали другие. Не буду прикладывать видео моего OpenGL viewer’а, по-моему интереснее смотреть сразу на Sketchfab: skfb.ly/6s6Ar
Рекомендуется открывать не больше одного ролика за раз, т.к. Sketchfab грузит в память сразу все кадры датасета, и вообще viewer у них не очень быстрый. Кстати, вот обещанный 4D котик (Вася):
Пёс Тотошка был не очень счастлив, что на него светят лазером. Но выбора у него не было:
Ещё несколько роликов есть в моём аккаунте на Sketchfab. Конечно, качество моделей можно улучшить если тщательно отфильтровать шумы от сенсора, можно уменьшить количество точек, чтобы проигрыватель на сайте не так тормозил, и т.п. Но как говорится, нет предела совершенству; я и так потратил на этот pet project много времени.
Да и вообще, учитывая агрессивное наступление AR и VR, я уверен что разработчики не обделят вниманием эти задачи. В сети встречается всё больше volumetric контента, как CG:
так и снятого в реальной жизни:
Согласитесь, выглядит весьма впечатляюще! В общем, за будущее free-viewpoint video переживать не приходится.
Напоследок нужно сказать, что весь код написанный для этого проекта доступен на Github под свободной лицензией. Хотя сгенерированные 4D ролики получились едва ли впечатляющими, у алгоритмов всё равно есть потенциал для дальнейшего использования и развития.
Главное преимущество описанного в статье подхода состоит в том, что 3D сцена генерируется на лету в realtime, в самом проигрывателе. Из-за этого в сжатом виде ролики могут занимать очень мало места, по сути почти столько же, сколько аналогичное традиционное видео.
Действительно, обычное RGB видео нужно нам только для текстур, а 3D координаты точек можно сохранять как разреженные карты глубины и тоже кодировать в видео-файл, уже в grayscale. Таким образом, для рендеринга одного кадра в 3D нам нужны только кадры из двух видео и немного метаданных (параметры камеры, и т.п.). На основе этого можно сделать прикольное приложение, скажем, Skype в augmented reality. Собеседника снимает depth-камера, а ваш iPhone в реальном времени рендерит говорящую 3D голову с помощью ARKit. Почти как голограммы из Star Wars.
Есть ещё вариант, который может пригодиться пользователям Tango. Дело в том, что Tango SDK предоставляет данные в виде облаков точек в 3D (как я и описывал выше), при этом для многих алгоритмов хочется иметь плотную карту глубины (depth map). Самый распространённый способ её получения — спроецировать точки на фокальную плоскость и проинтерполировать значения глубины между соседними точками, в которых оно известно. Так вот комбинация триангуляции Делоне + OpenGL позволяет делать эту интерполяцию точно и эффективно. За счёт того, что растеризация происходит на GPU, можно генерировать карты глубины в высоком разрешении даже на смартфоне.
Но это всё лирика. Пока что я просто очень рад что дописал статью. Если есть какие-то мысли или фидбек, предлагаю обсудить в комментариях.
Image credits
Автор: Petrenuk
