Статья написана об использовании алгоритма вычисления расстояния Левенштейна для нечеткого поиска в тексте, без использования вспомогательного словаря.
Расстояние Левенштейна используется для сравнения двух слов или двух строк, чтобы определить их схожесть. Некоторое время назад передо мной встала схожая задача — в заданной строке искать вхождение слов, словосочетаний и формул, похожих на образец.
Об алгоритме Вагнера-Фишера я читал, но сохранить его куда-либо не догадался (в отпуск же собрался). И вот, под стук колес я рисую матрицы. Как уснешь, когда редакционное расстояние между словами не считается. После получения удовлетворительного результата, я записываю алгоритм на бумажку и, с чувством выполненного долга, засыпаю.
На следующий день, после сравнения записей и реального алгоритма я обнаружил в них небольшое различие, меняющее область применения задачи. Если оригинальный алгоритм подходит для сравнения двух слов и определения «сколько символов одного слова нужно удалить/добавить/заменить, чтобы получилось второе слово», то мутировавший решает другую задачу — «сколько символов первой строки нужно удалить/добавить/заменить, чтобы она целиком вошла во вторую строку». Подобных реализаций алгоритма я не встречал, если применяется где-то — пишите.
Для начала — сам алгоритм Вагнера-Фишера для вычисления расстояния Дамерау-Левенштейна. Почитать можно тут и тут.
Пример исходного кода взят из wiki.
В нем переименованы row в column, чтобы иллюстрации совпадали с кодом.
def distance(a, b):
"Calculates the Levenshtein distance between a and b."
n, m = len(a), len(b)
if n > m:
# Make sure n <= m, to use O(min(n,m)) space
a, b = b, a
n, m = m, n
current_column = range(n+1) # Keep current and previous column, not entire matrix
for i in range(1, m+1):
previous_column, current_column = current_column, [i]+[0]*n
for j in range(1,n+1):
add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1]
if a[j-1] != b[i-1]:
change += 1
current_column[j] = min(add, delete, change)
return current_column[n]
print distance(u'аргумент', u'рудимент') # 4
print distance(u'весомый аргумент в мою пользу', u'рудимент') # 25
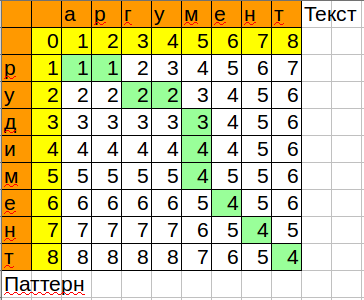
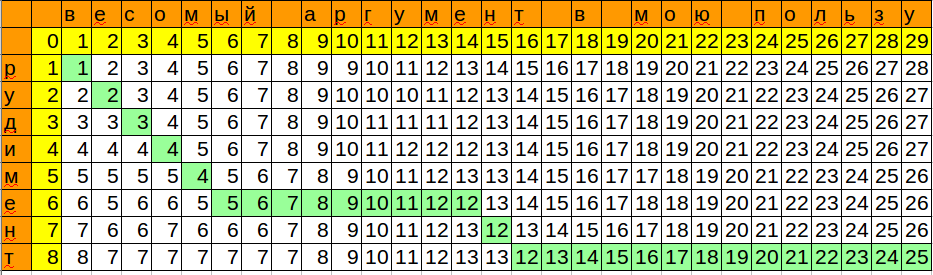
Формула для воспроизведения в calc/excel:
=MIN(B3+1;C2+1;B2+IF($A3=C$1;0;1))
Обратите внимание, как алгоритм оптимизирован по памяти, хранятся только текущая и предыдущая колонка.
Задача поиска отличается от задачи сравнения тем, что нам не важно, что было до совпадения и что будет после. Потому:
— начальная цена сопоставления с текущим символом текста равна нулю, а не позиции этого символа
— результатом является не правый нижний угол таблицы, а минимальное значение в последней строке
— оптимизация, при которой может произойти замена текста и искомого шаблона (если искомый шаблон длиннее текста), здесь лишняя
def distance_2(text, pattern):
"Calculates the Levenshtein distance between text and pattern."
text_len, pattern_len = len(text), len(pattern)
current_column = range(pattern_len+1)
min_value = pattern_len
end_pos = 0
for i in range(1, text_len+1):
previous_column, current_column = current_column, [0]*(pattern_len+1) # !!!
for j in range(1,pattern_len+1):
add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1]
if pattern[j-1] != text[i-1]:
change += 1
current_column[j] = min(add, delete, change)
if min_value > current_column[pattern_len]: # !!!
min_value = current_column[pattern_len]
end_pos = i
return min_value, end_pos
print distance_2(u'аргумент', u'рудимент') #3, 8
print distance_2(u'весомый аргумент в мою пользу', u'рудимент') #3, 16
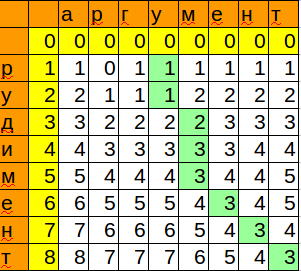
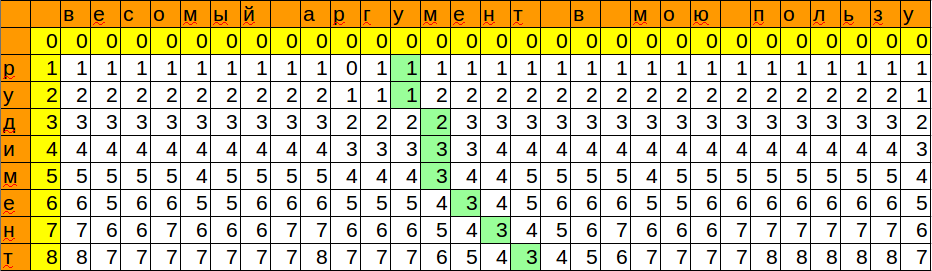
Мы запомнили позицию и минимальное значение, которое получили при сопоставлении шаблона с очередным символом. Таким образом, мы получили место, куда можно с минимальными изменениями вставить наше слово.
Последний штрих — получить всю информацию по совпадению.
def distance_3(text, pattern):
min_value, end_pos = distance_2(text, pattern)
min_value, start_pos = distance_2(text[end_pos-1::-1], pattern[::-1])
start_pos = end_pos - start_pos
return min_value, start_pos, end_pos, text[start_pos:end_pos], pattern
print distance_3(u'аргумент', u'рудимент') # 3 3 8 умент рудимент
print distance_3(u'весомый аргумент в мою пользу', u'рудимент') # 3 11 16 умент рудимент
P.S.: В «Тёмная комната» проще найти «Чёрная кошка», чем «Белый питбуль».
print distance_3(u'Тёмная комната', u'Чёрная кошка') # 4 1 12 ёмная комна Чёрная кошка
print distance_3(u'Тёмная комната', u'Белый питбуль') # 12 6 7 Белый питбуль
Автор: kotbajan






