Лежит на струнах пыль
Ржавеет под окном
Разбитый телевизор
Ты сгладил все углы
И жизнь твоя сплошной
Проклятый компромисс
Ни вверх ни вниз
Так поёт группа Би-2 в песне "Компромисс" и с ними трудно не согласиться. Наша жизнь действительно состоит из сплошных проклятых компромиссов между несколькими решениями. Мы пытаемся найти максимально дешёвую, но качественную электронику, ищем экономичный, но быстрый автомобиль и красивого, но надёжного партнёра для отношений.
Каждая из этих повседневных задач заключается в поиске оптимума нескольких конфликтующих между собой функций. Это называется многокритериальная оптимизация (Multi-objective optimization). В этой статье мы ближе познакомимся с этой задачей, посмотрим на 2 популярных метода её решения и узнаем, как с её помощью (не)заработать на криптовалюте с минимальным риском.
Привет! Меня зовут Артём, я Data Scientist и последние несколько месяцев я изучал применение методов многокритериальной оптимизации в машинном обучении. Сейчас хочу познакомить вас с этой интереснейшей задачей и показать довольно забавный пример её применения.
Я очень старался сделать статью максимально понятной для широкого круга читателей, но я довольно часто использую определение "Генетический алгоритм". Это интересная и полезная штука о которой можно почитать тут и посмотреть хороший курс Сергея Балакирева тут. Это облегчит восприятие статьи. Но в целом, генетические алгоритмы можно воспринимать, как просто чёрный ящик, который находит наименьшую точку любой функции.
Постановка задачи
Сама по себе оптимизация - это процесс поиска экстремума (максимальной или минимальной точки) некоторой функции.
По данным википедии, многокритериальная оптимизация - это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения. Проще говоря, это процесс поиска таких решений, которые максимально удовлетворяют два и более критерия.
К слову, в некоторых источниках есть довольно специфическое разделение на мультикритериальную и многокритериальную оптимизацию (мulti-objective и many-objective соответственно). Обычно имеют ввиду, что при мультикритериальной оптимизации мы оптимизируем 2 функции, а при многокритериальной больше 2. Мы опустим это разделение.
Чтобы лучше понять, чем мы тут будем заниматься, нужно ввести несколько терминов: Парето-доминирование, Парето-фронт и Парето-оптимум, но сначала...
30 секунд или 1 минута исторической справки
Наверняка у вас возник вопрос, кто такой Парето, в честь которого названы эти термины.

Речь о Вильфредо Федерико Дамасо Парето, итальянском экономисте и социологе, который предложил термин эффективности по Парето. Это состояние системы, при котором ни один показатель системы не может быть улучшен без ухудшения другого показателя.
Важные термины
Почти все алгоритмы многокритериальной оптимизации оперируют таким термином, как Парето-доминирование. Так называют отношение между двумя решениями. Одно решение (назовём его X) доминирует другое решение (допустим Y), если X не хуже решения Y ни по одному условию и обязательно лучше Y, хотя-бы по одному.
Допустим, у нас есть машины A, B, C. Машина A разгоняется до 100 км/ч за 10 секунд и сжигает 6 литров бензина за 100 км.
Машина B тоже разгоняется до сотни за 10 секунд, но потребляет уже 6.5 литров бензина на 100 км.
Мы хотим минимизировать время разгона до сотни и потребление бензина. Это наши 2 критерия.
Следовательно, машина А доминирует машину B т.к. она (A) имеет разгон не хуже чем у машины B, но при этом она кушает меньше бензина.
А вот машина C разгоняется до 100 всего за 5 секунд, но и жрёт 10 литров/100 км. Получается, что она не доминирует машину A, т.к. она хуже машины А по потреблению бензина, но быстрее разгоняется до сотни.
Ещё один важный момент заключается в том, что решением задачи многокритериальной оптимизации является множество решений, которые не доминируют друг друга. Это множество называется Парето-фронтом.
Очень редко получается так, что у задачи есть одно решение, максимально удовлетворяющее каждому критерию. По этому, каждый элемент Парето-фронта представляет собой компромисс между значениями нескольких целевых функций.
Вернёмся к нашему примеру с автомобилями:
В данной ситуации в парето-фронт войдут машины A и C, т.к. они не доминируют друг друга. Машина B, в свою очередь, в парето-фронт не попадёт т.к. она прожорливее, чем A, хотя имеет ту же скорость разгона.Машина А представляет собой решение с минимальным расходом бензина из всех доступных, а машина C с максимальной скоростью разгона. Выбирать между ними уже предстоит человеку. Задача алгоритма - найти лучшие компромиссы.
Парето-оптимум - ещё одно понятие, которое просто обозначает любое решение на парето-фронте. Это такой вариант, который нельзя улучшить ни по одному из критериев, не ухудшив другие.
Самопроверка
Если у вас есть желание проверить, правильно ли вы поняли принцип формирования парето-фронта, то предлагаю вам выполнить следующее задание:

Дано 6 вымышленных моделей телефонов, их цена и их производительность в каких-то пунктах. Мы хотим минимизировать цену, но при этом максимизировать производительность, чтобы телефон тянул Genshin Impact. Определите, какие телефоны парето-оптимальны.
Ответ
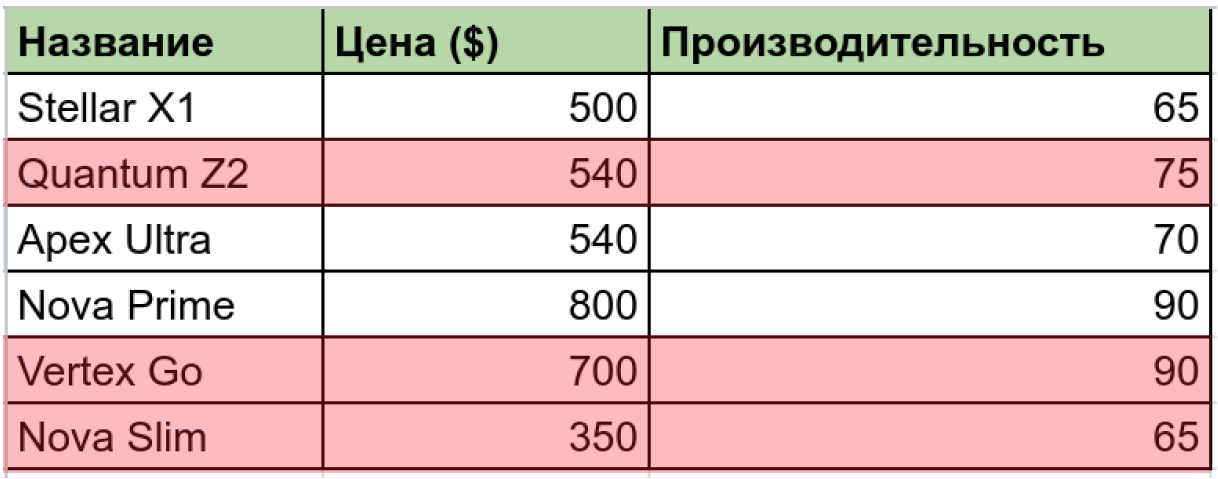
Vertex Go оптимален т.к. предлагает самую высокую производительность, но дешевле конкурентов в своём сегменте. Quantum Z2 оптимален по той же логике. А Nova Slim самый дешёвый.
Подходы к решению задачи
Теперь, когда мы поняли, какую задачу решаем, перейдём к методам её решения. Их много, они разные и нужно попытаться их классифицировать. Я выделил такие способы многокритериальной оптимизации:
-
Методы скаляризации
-
Эволюционные алгоритмы
-
Алгоритмы локального поиска
-
Точные (детерминированные) методы
-
Интерактивные методы
Идея скаляризации сводится к тому, чтобы превратить многокритериальную оптимизацию в однокритериальную. Самый простой и понятный вариант - взвешенная сумма, когда каждая цель умножается на свой коэффициент (вес), и результаты суммируются в одну целевую функцию.
В нашей задаче с машинами мы могли бы сказать, что для нас расход бензина (consumption) важнее разгона до сотни (acceleration) и преобразовали бы две функции в одну вот такую:
А функции такого вида мы умеем оптимизировать, например, градиентным спуском (если можем взять производную), методами байесовской оптимизации или генетическим алгоритмом.
Алгоритмы многокритериальной оптимизации, основанные на популяционных методах, вдохновлены процессом эволюции. Они используют генетические операторы скрещивания, мутации и естественного отбора для поиска глобального оптимума функции. По сути, они являются хитрыми модификациями генетического алгоритма (жутко интересная штука. Рекомендую почитать о ней отдельно, чтобы лучше понять о чём дальше будет идти речь).
Примеры таких алгоритмов: NSGA-II, SPEA2, MOEA/D
Алгоритмы локального поиска «шаг за шагом» перемещаются по пространству решений, пытаясь найти набор Парето-оптимальных вариантов. Они также используют разные метаэвристические алгоритмы.
Примеры: PSA (Многокритериальная имитация отжига), Pareto Tabu Search
Точные (детерминированные) методы – это такие алгоритмы, которые опираются на строгие математические свойства задачи и дают гарантированно оптимальное решение при условии, что все входные данные заданы точно (то есть без случайных отклонений). Эти алгоритмы обычно очень требовательны по вычислительным ресурсам и нужно, чтобы функции были дифференцируемыми.
В интерактивных алгоритмах, например NIMBUS, пользователь (или эксперт) активно участвует в процессе оптимизации, указывая предпочтения или корректируя цели по ходу работы алгоритма. Это позволяет постепенно сузить пространство решений до наиболее приемлемых для конкретного случая.
Так, с классификацией разобрались... Теперь поближе познакомимся с 2 популярными эволюционными алгоритмами многокритериальной оптимизации: MOEA/D и NSGA-II
Знакомство с MOEA/D
MOEA/D или Multiobjective Evolutionary Algorithm Based on Decomposition это эволюционный алгоритм многокритериальной оптимизации, идея которого заключается в том, что многокритериальную задачу можно разбить на множество скалярных подзадач. Для этого каждой подзадаче сопоставляется весовой вектор , который определяет приоритеты для каждого критерия.
Так в примере про машины весовой вектор выглядел бы так:
[0.7, 0.3]т.к. экономичность важнее разгона.

В начале работы алгоритма мы задаём набор весовых векторов, которые будут указывать направление для оптимизации. На схеме эти вектора показаны буквой . Чем их больше - тем детальнее алгоритм изучит пространство вариантов.
После этого, скаляризуем задачу и запускаем столько генетических алгоритмов, сколько у нас получилось подзадач. Каждый из этих алгоритмов оптимизирует свою функцию и находит её оптимум. Из оптимумов каждой подзадачи и складывается итоговый парето-фронт.
Ещё одна важная особенность MOEA/D в том, что соседние подзадачи взаимодействуют между собой. Когда генерируется новое решение, оно оценивается для каждой подзадачи в пределах заданного соседства. Если кандидат улучшает скаляризованную функцию для данной подзадачи, он заменяет текущее решение. За счёт этого мы ускоряем сходимость алгоритма и позволяем более широко исследовать пространство вариантов.
Преимущества этого алгоритма заключаются в высокой вычислительной эффективности и равномерном покрытии парето-фронта. Также, он отлично работает на задачах с большим количеством целевых функций. Из недостатков могу отметить непредсказуемое поведение на сложных парето-фронтах и чувствительность к настройке соседства. Если поставить слишком большое число соседей, то есть риск, что какое-то одно решение поглотит другие, что снизит разнообразие.
Знакомство с NSGA-II
Другой подход к решению задачи многокритериальной оптимизации предлагает алгоритм NSGA-II (Non-dominated Sorting Genetic Algorithm II). Это обычный генетический алгоритм, с хитро изменённым подходом к отбору особей для размножения.

В классической реализации генетического алгоритма используется турнирный отбор или отбор рулеткой в зависимости от значения целевой функции (в генетических алгоритмах она называется функцией приспособленности). Так мы приходим к тому, что потомство оставляют только 50% самых приспособленных решений и за счёт этого происходит оптимизация.
В NSGA-II мы действуем интереснее. Первоначально мы используем алгоритм Non-dominated Sorting. Он разделит всю популяцию на несколько парето-рангов (они показаны буквой F на картинке). Логика там такая, что особи из 1 ранга не доминируют друг друга и их не доминирует вообще никто в популяции. Особи из 2 ранга также не доминируют друг друга, но их доминируют только особи из 1 ранга. Особей из 3 ранга доминируют только особи из 1 и 2 рангов и так далее... Чем выше ранг, тем приоритетнее особи из него попадают в команду для размножения.
Но, как мы видим на картинке, может получиться, что не всем особям одного ранга хватит мест в новом поколении. Тогда мы включаем алгоритм Crowding distance sorting. Его суть в том, чтобы выбрать для размножения самые отдалённые от основного скопления решения. Это позволяет разнообразить популяцию и ускорить сходимость.
Много-много раз мы повторяем эти операции и, в итоге, получаем разнообразный парето-фронт с хорошим покрытием. Красота!
Проблема в том, что NSGA-II предназначен исключительно для решения задач с 2 целевыми функциями. Также этот алгоритм довольно вычислительно сложный (сложность Non-dominated Sorting - ). Но у NSGA-II есть модификации (например NSGA-III), которые позволяют работать с большим числом функций.
Как на этом заработать?
Окей, вот мы разобрались с тем, как можно оптимизировать несколько функций, но как извлечь выгоду из этого знания?
Представим, что вы выиграли в лотерею 10000$ и вы, как финансово грамотный человек, решили не прогулять их, а вложить... в криптовалюту! Подойти к этому нужно с умом и вы решили воспользоваться алгоритмами многокритериальной оптимизации для формирования идеального криптовалютного портфеля.
Осмыслив ситуацию, вы выдвинули следующую гипотезу: "Если портфель показал высокую доходность за последние месяцев, то и в следующем месяце он даст нам заработать". Но вы помните, что криптовалюты очень волатильны и их курс может быстро меняться.
Так мы и приходим к задаче многокритериальной оптимизации криптовалютного портфеля: мы хотим получить такое распределение активов, которое давало максимальный рост цены и, при этом, минимальную корреляцию между курсами активов, чтобы при обвале одной монеты не потерять все остальные деньги.
Я предлагаю представить криптовалютный портфель в виде вектора следующего вида: [0.089, 0.23 , 0.109, 0.118, 0.116, 0.108, 0.116, 0.114], где каждое число обозначает долю какой-то монеты в портфеле. В сумме все доли должны давать 1. Задачей нашего алгоритма будет найти набор таких компромиссных векторов.
Цены токенов будем вытягивать с Yahoo Finance с помощью библиотеки yfinance для Python.
Полный код эксперимента лежит у меня на github
import yfinance as yf
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
# Функция для получения цены актива на указанную дату
def get_price_on_date(ticker_symbol: str, date_str: str) -> float | None:
try:
date = datetime.strptime(date_str, '%Y-%m-%d')
# Запрашиваем данные за сутки (чтобы получить цену закрытия нужного дня)
end_date = (date + timedelta(days=1)).strftime('%Y-%m-%d')
data = yf.Ticker(ticker_symbol).history(start=date_str, end=end_date)
if data.empty:
print(f"Нет данных по {ticker_symbol} на дату {date_str}")
return None
return round(float(data['Close'].iloc[0]), 2)
except Exception as e:
print(f"Ошибка при получении цены для {ticker_symbol}: {e}")
return None
# Загрузим историю изменения цены криптовалюты
# Список интересующих криптовалют можно изменять. Все доступные тикеры можно посмотреть на https://finance.yahoo.com/crypto/
TICKERS = ["TON11419-USD", "SUI20947-USD", 'ETH-USD', "LINK-USD", "APT21794-USD", "FET-USD", "TAO22974-USD", 'BTC-USD', 'USDT-USD']
# Даты обучающей выборки (оптимизационный период)
training_start_date = "2024-08-01"
training_end_date = "2025-01-29"
# Получаем цены на начало и конец периода оптимизации
start_token_prices = {ticker: get_price_on_date(ticker, training_start_date) for ticker in TICKERS}
end_token_prices = {ticker: get_price_on_date(ticker, training_end_date) for ticker in TICKERS}
# Загрузка исторических данных (цен закрытия) для расчёта ожидаемой доходности и ковариационной матрицы
data: pd.DataFrame = yf.download(TICKERS, start=training_start_date, end=training_end_date, progress=True)['Close']
Теперь нужно определиться с тем, как будем считать доходность и уровень риска портфеля. Это задача творческая, поделюсь своим видением.
Казалось бы, доходность портфеля можно посчитать просто как разницу конечной цены и начальной, но в такой ситуации мы будем жёстко привязаны к промежутку времени и у алгоритма будет плохая обобщающая способность. Я решил, что правильнее будет разбивать период оптимизации на несколько сегментов и считать среднее их доходности. Это позволит дать алгоритму представление о том, как вёл себя портфель в разных ситуациях.

Риск портфеля () определяется как корень квадратный из произведения транспонированного вектора весов, ковариационной матрицы и самого вектора весов. Это помогает оценить, насколько волатильны изменения цен активов при данном распределении:
Где - наш вектор долей актива в портфеле (
- его транспонированный брат), а
- ковариационная матрица, которая показывает, как между собой связаны изменения цены активов. Она помогает увидеть то, какие активы растут вместе, какие компенсируют друг друга, а какие существуют совсем без логики.
Ещё, в книжке по финансовой грамотности я читал про то, что нельзя класть все яйца в одну корзину и решил добавить алгоритму штраф, за высокую концентрацию инвестиций. Для этого я использовал индекс Херфиндаля — Хиршмана:
Где - доля той или иной монеты в портфеле. Чем больше данный коэффициент - тем хуже он диверсифицирован.
Итого, функция риска выглядит вот так:
Реализовывать алгоритмы я буду с помощью библиотеки PyMoo. Код, описывающий задачу, которую будем оптимизировать тут:
Код (длинный)
# Класс для решения задачи многокритериальной оптимизации криптовалютного портфеля
class CryptoPortfolioProblem(ElementwiseProblem):
"""Задача многокритериальной оптимизации криптовалютного портфеля."""
START_PRICE = 1000.0 # начальный капитал
def __init__(self, elementwise=True, **kwargs):
"""
Инициализация задачи оптимизации.
Args:
elementwise (bool): Флаг поэлементной оценки
**kwargs: Дополнительные параметры
"""
n_assets = len(TICKERS)
# Предварительный расчет статических данных (в том числе цен для подпериодов)
self._precompute_data()
super().__init__(
elementwise=elementwise,
n_var=n_assets,
n_obj=2,
xl=0,
xu=1
)
def _precompute_data(self):
"""
Предварительный расчет данных для повышения производительности.
Здесь сохраняются:
- цены на начало и конец периода,
- ковариационная матрица,
- цены для промежуточных дат (подпериодов), по которым будет рассчитываться средняя доходность.
"""
# Сохраняем цены на начало и конец периода по каждому активу
self.start_token_prices = np.array([start_token_prices[ticker] for ticker in TICKERS])
self.end_token_prices = np.array([end_token_prices[ticker] for ticker in TICKERS])
self.cov_matrix = cov_matrix.values
# Задаём число подпериодов для расчёта (например, 4 подпериода -> 5 точек: начало, 3 промежуточные и конец)
self.n_subperiods = 7
# Преобразуем даты оптимизационного периода в объекты datetime
start_dt = datetime.strptime(training_start_date, '%Y-%m-%d')
end_dt = datetime.strptime(training_end_date, '%Y-%m-%d')
total_days = (end_dt - start_dt).days
# Определяем равномерно распределённые даты (точки) внутри периода (включая начальную и конечную)
subperiod_dates = []
for i in range(self.n_subperiods + 1):
# Вычисляем количество дней для текущей точки (округляем до целого)
delta_days = round(i * total_days / self.n_subperiods)
sub_dt = start_dt + timedelta(days=delta_days)
subperiod_dates.append(sub_dt.strftime('%Y-%m-%d'))
# Вспомогательная функция для получения цен по всем активам на указанную дату
def get_prices_for_date(date_str: str) -> np.ndarray:
prices = []
for ticker in TICKERS:
p = get_price_on_date(ticker, date_str)
if p is None:
raise ValueError(f"Нет данных по {ticker} на дату {date_str}")
prices.append(p)
return np.array(prices)
# Получаем и сохраняем цены для каждого выбранного подпериода в виде numpy-массива
# Размерность массива: (число точек, число активов)
self.subperiod_prices = np.array([get_prices_for_date(d) for d in subperiod_dates])
@staticmethod
def _normalize_weights(x: np.ndarray) -> np.ndarray:
"""Нормализация весов портфеля так, чтобы их сумма была равна 1."""
return x / np.sum(x)
def _evaluate(self, x: np.ndarray, out: dict, *args, **kwargs) -> None:
"""
Оценка целевых функций:
- первая цель: максимизация доходности (минимизируем отрицательное значение доходности),
- вторая цель: минимизация риска (волатильности + индекс концентрации).
Args:
x: Вектор весов портфеля
out: Словарь с результатами оптимизации
"""
weights = self._normalize_weights(x)
profit = self._calc_portfolio_return(weights)
risk = self._calc_volatility(weights)
out["F"] = [-profit, risk]
def _calc_portfolio_return(self, weights: np.ndarray) -> float:
"""
Расчёт доходности портфеля как средней процентной доходности по заданным подпериодам.
Логика:
1. Рассчитываем количество единиц каждого актива, которые покупаются на начальную сумму.
2. Вычисляем стоимость портфеля в каждую из равномерно распределённых точек периода (с использованием заранее
загруженных цен по подпериодам).
3. Для каждого подпериода (между соседними точками) рассчитываем процентное изменение стоимости.
4. Возвращаем среднее арифметическое процентных изменений как меру доходности.
Args:
weights: Нормализованные веса активов в портфеле.
Returns:
float: Средняя процентная доходность портфеля за подпериоды.
"""
# Рассчитываем число единиц каждого актива, приобретённых на начальный капитал по цене в начале периода
portfolio_units = weights * self.START_PRICE / self.start_token_prices
# Вычисляем стоимость портфеля для каждой из точек (подпериодов)
# Для каждой даты суммируем: количество единиц * цена актива в эту дату
portfolio_values = np.dot(self.subperiod_prices, portfolio_units)
# Вычисляем процентные изменения (доходность) между соседними подпериодами:
# (стоимость в конце подпериода - стоимость в начале подпериода) / стоимость в начале подпериода
subperiod_returns = (portfolio_values[1:] - portfolio_values[:-1]) / portfolio_values[:-1]
# Возвращаем среднее арифметическое процентных изменений как итоговую доходность портфеля
avg_return = np.mean(subperiod_returns)
return avg_return
def _calc_diversification(self, weights: np.ndarray) -> float:
"""
Расчёт индекса Херфиндаля-Хиршмана для оценки концентрации портфеля.
Args:
weights: Нормализованные веса активов.
Returns:
float: Значение индекса концентрации.
"""
return np.sum(weights ** 2)
def _calc_volatility(self, weights: np.ndarray) -> float:
"""
Расчёт риска портфеля как суммы стандартного отклонения (на основе ковариационной матрицы)
и меры концентрации (индекса Херфиндаля-Хиршмана).
Args:
weights: Нормализованные веса активов.
Returns:
float: Мера риска портфеля.
"""
return np.sqrt(weights.T @ self.cov_matrix @ weights) + self._calc_diversification(weights)
# Создаем экземпляр задачи оптимизации
problem = CryptoPortfolioProblem()Далее, приступим к самой оптмизации и натравим на наш криптовалютный портфель NSGA-II:
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.operators.mutation.pm import PolynomialMutation
from pymoo.optimize import minimize
AMOUNT_OF_SOLUTIONS = 100 # К-во особей в популяции
MUTATION_PROB = 0.1 # Вероятность случайной мутации
AMOUNT_OF_GENERATIONS = 2000 # К-во поколений
nsga2 = NSGA2(pop_size=AMOUNT_OF_SOLUTIONS)
mutation = PolynomialMutation(eta=20,
prob_var=MUTATION_PROB)
nsga2_result = minimize(
problem, # Выбираем задачу
nsga2, # Выбираем алгоритм
('n_gen', AMOUNT_OF_GENERATIONS),
mutation=mutation # Выбираем метод мутации
)
Забавная штука с тем, что в PyMoo можно только минимизировать функции. Из-за этого мы умножаем прибыль на -1, чтобы алгоритм работал корректно.
Когда мы выполним эту ячейку кода, то запустится оптимизация. Мы можем визуализировать её результаты и получить примерно такой парето-фронт:
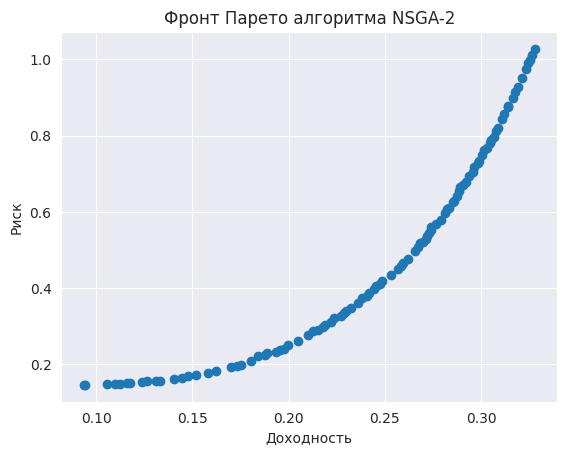
К анализу результатов придём чуть позже, а сначала запустим MOEA/D на тех же данных:
# get_reference_directions генерирует векторы направления для MOEA/D
AMOUNT_OF_DIRECTIONS = 50 # К-во подзадач
N_NEIGHBORS = 5 # К-во соседних подзадач, которые могут обмениваться решениями
AMOUNT_OF_GENERATIONS = 2000 # К-во поколений
ref_dirs = get_reference_directions('uniform', 2, n_partitions=AMOUNT_OF_DIRECTIONS)
moea_d = MOEAD(
ref_dirs,
n_neighbors=N_NEIGHBORS,
)
moea_d_result = minimize(problem,
moea_d,
('n_gen', AMOUNT_OF_GENERATIONS),
verbose=SHOW_LOGS
)
И получаем вот такой, более смещённый к центру парето-фронт:
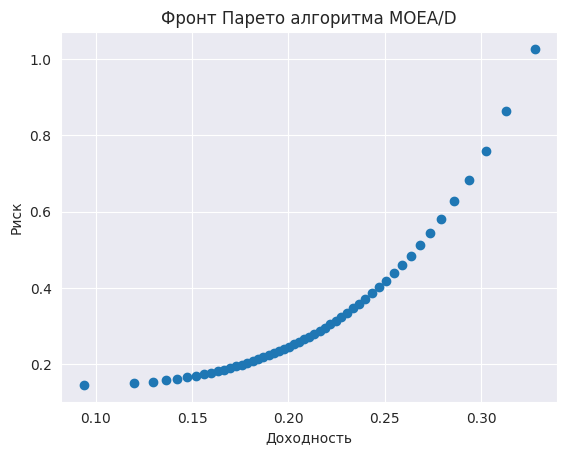
А теперь рассмотрим те портфели, которые составили для нас алгоритмы и сравним их между собой:
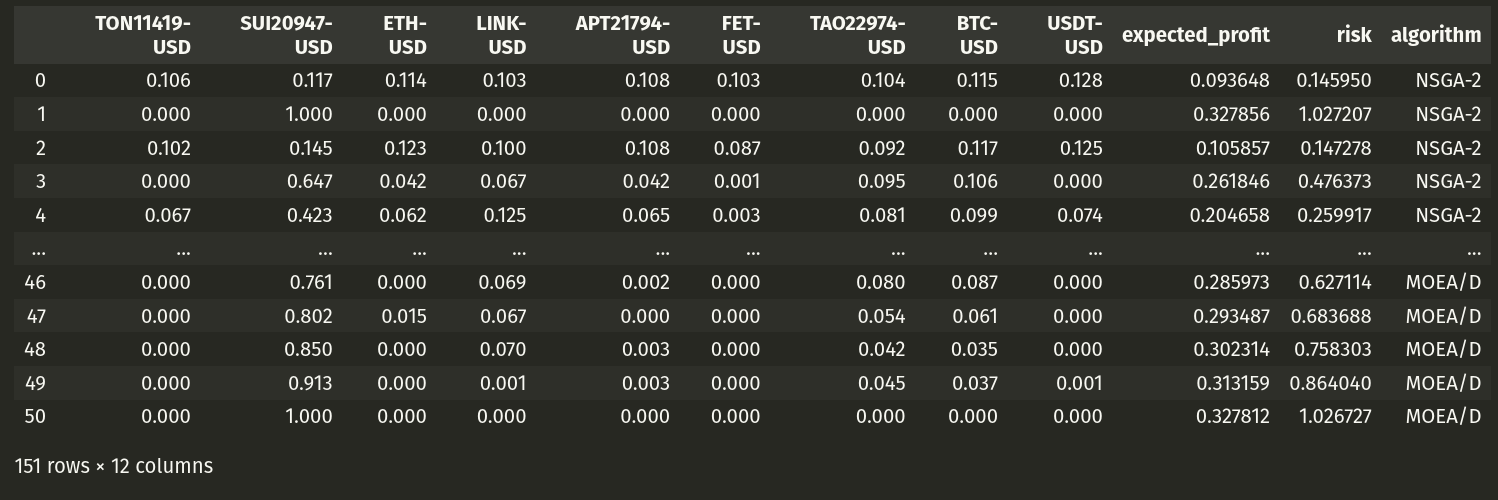
Если сгруппировать портфели по алгоритмам и посмотреть на средние значения, то окажется, что NSGA-II предлагает, в среднем, чуть более прибыльные решения: 0.211% у MOEA/D против 0.24% у NSGA-II, но и более рискованные: 0.331 очков риска у MOEA/D против 0.49 очков у NSGA-II.
В остальном, всё примерно одинаково. Единственное, NSGA-II решил, что SUI более привлекательный актив и вкладывал в него почти 60% средств. MOEA/D сильнее диверсифицировал свой портфель.

Если посмотреть на максимальную доходность портфеля, то окажется, что оба алгоритма получили примерно 33%.

Такую оценку получили решения, в которых 100% средств вложено в SUI...

Скорее всего, это связано с тем, что SUI показывал сильный рост в период оптимизации и алгоритм "запомнил", что вкладываться нужно в него. График курса SUI это подтверждает:
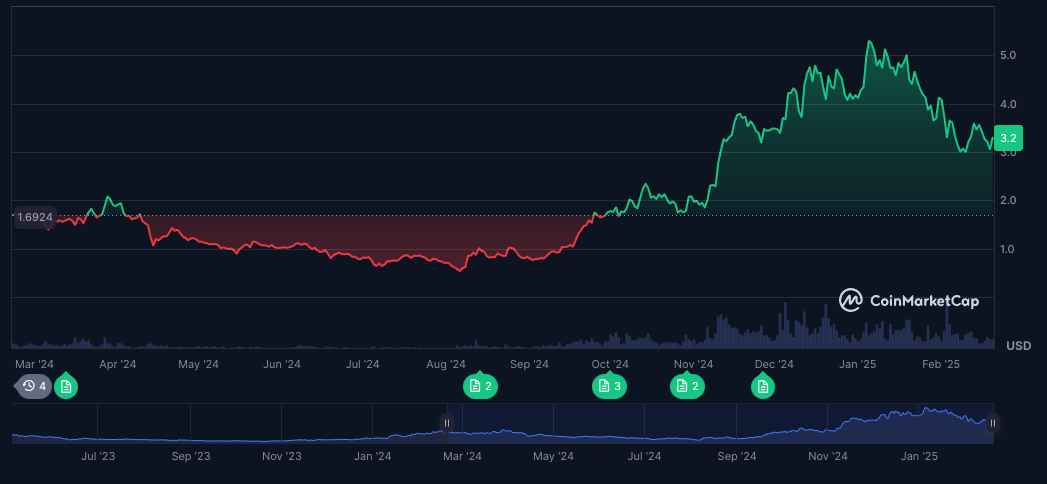
Минимальную оценку риска, в свою очередь, получили те портфели, где сумма поровну распределена среди всех активов.
А теперь - самое интересное. Вот мы оптимизировали криптопортфель на данных о курсе монет с 1 августа 2024 по 30 января 2025. 1 февраля 2025 года мы решились и вложили лотерейные 10000$ в соответствии с рекомендацией алгоритма. Сколько бы мы заработали на момент написания статьи (19 февраля)?
-1043,2$ в лучшем случае
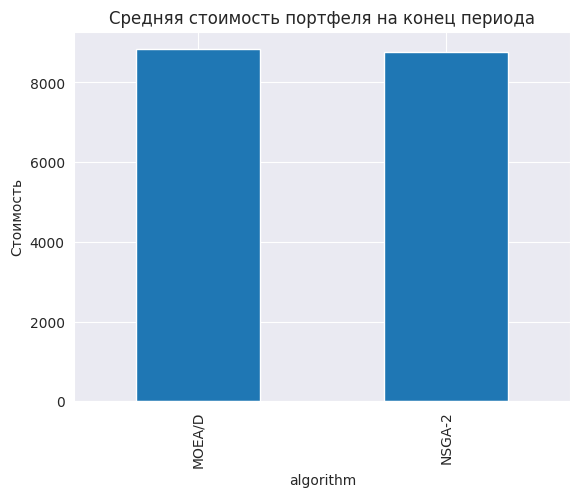
В среднем, стоимость криптопортфеля на конец нашего тестового периода упала на 1500$ или на 15%. Думаю, что это обусловлено падением всего крипторынка в феврале 2025.

Интересно получилось, что чем выше прибыль на тестовом периоде предполагал алгоритм, тем ниже оказалась реальная прибыль. Думаю, это связано с тем, что сверхдоход связан скорее с аномальными и единоразовыми событиями, которые врядли повторятся ещё. А вот диверсифицированные портфели ведут себя максимально предсказуемо.
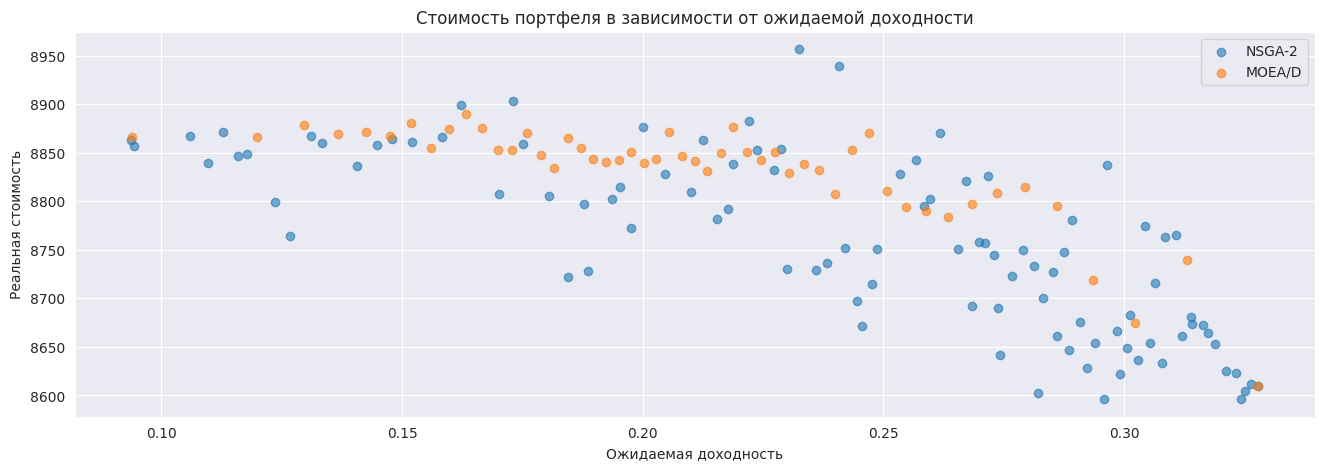
Об этом же свидетельствует и график зависимости итоговой стоимости от уровня риска. Диверсификация - это важно.

Заключение
Вот примерно так мы познакомились с задачей многокритериальной оптимизации. Как по мне, эта тема незаслуженно обделена вниманием инженеров и исследователей. Хотя в этом направлении тоже есть подвижки! Так, например, в библиотеке Optuna для подбора гиперпараметров моделей машинного обучения появились алгоритмы NSGA-II и NSGA-III. Простор для исследования остаётся также в области использования алгоритмов многокритериальной оптимизации для Feature Selection и подборе архитектуры нейронных сетей.
Я надеюсь, что моя статья была вам интересна и полезна. Приглашаю вас поделиться мнением в комментариях, задать вопросы, а также подписаться на мой телеграм-канал, где я пишу о машинном обучении, искусственном интеллекте и нашем будущем.
Также, напоминаю, что код этого эксперимента целиком доступен на GitHub в формате Jupyter ноутбука. Если у вас есть идеи и предложения по улучшению этого эксперимента - я готов принимать Pull Requests.
Автор: artyom08112006






