В нашей реальности мы никогда не имеем полных исходных данных для задач, которые на бумаге кажутся чисто математическими. Вот пример из практики одного из регионов с магазином. В июне вам звонят с радио и говорят, что готовы повторить размещение рекламы со скидкой 40%. Это 192 ролика за две недели. Прошлый раз вы заказывали эту рекламу «на попробовать», поскольку матожидание прибыли превышало затраты на рекламу.
Проблема в том, что за период размещенния случилось две большие вещи:
- Из-за праздников был сезонный спад, и продажи по городам падали.
- Реклама должна была дать дополнительные продажи.
Сейчас нужно отделить одно от другого и понять, что и как сработало. Нельзя оценивать рекламу без учёта спада, и спад без учёта рекламы. Вот ваш график продаж за период до праздников, во время и после:
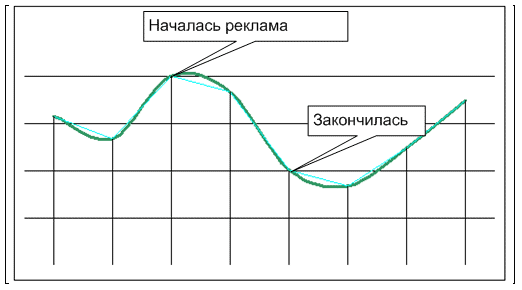
Исходный город, продажи в штуках по вертикали к неделям по горизонтали
По нему видно, что продажи падают после рекламы на праздниках. Падение на праздники — норма для всех городов. Правда, мы, грубо говоря, не знаем, какой бы график был без рекламы. Такой же? Немного ниже? Сильно ниже?
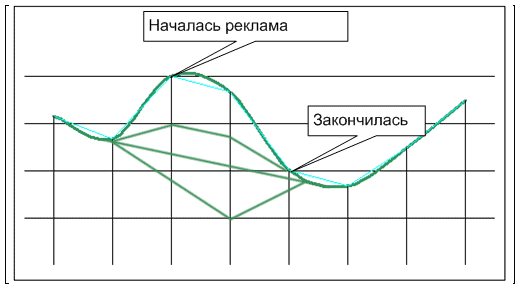
Без рекламы события шли бы по одному из этих сценариев. По какому — я не знаю.Читать полностью »