И снова здравствуйте! Сегодня я продолжаю серию статей в блоге Surfingbird, посвящённую разным методам рекомендаций, а также иногда и просто разного рода вероятностным моделям. Давным-давно, кажется, в прошлую пятницу летом прошлого года, я написал небольшой цикл о графических вероятностных моделях: первая часть вводила основы графических вероятностных моделей, во второй части было несколько примеров, часть 3 рассказывала об алгоритме передачи сообщений, а в четвёртой части мы кратко поговорили о вариационных приближениях. Цикл заканчивался обещанием поговорить о сэмплировании — ну что ж, не прошло и года. Вообще говоря, в этом мини-цикле я поведу речь более предметно о модели LDA и о том, как она помогает нам делать рекомендации текстового контента. Но сегодня начну с того, что выполню давнее обещание и расскажу о сэмплировании в вероятностных моделях — одном из основных методов приближённого вывода.

Читать полностью »
Метка «теория вероятностей»
Вероятностные модели: сэмплирование
2014-06-20 в 11:52, admin, рубрики: data mining, Алгоритмы, байесовские сети, Блог компании Surfingbird, искусственный интеллект, математика, математическое моделирование, сэмплирование, теория вероятностей, метки: data mining, байесовские сети, математика, математическое моделирование, сэмплирование, теория вероятностейТеория вероятностей против интуиции
2014-05-31 в 8:07, admin, рубрики: математика, теория вероятностей, метки: теория вероятностейНачну я этот пост с того, что устрою небольшой холивар. Рассмотрим такую задачу (которая может показаться очень знакомой):
Вы участвуете в телевизионном шоу. В последнем раунде перед вами три двери, за одной находится овца, за другой — козел, а за третьей — Феррари. Вы хотите Феррари, и не хотите ни кого из крупного рогатого скота. Ведущий предлагает вам выбрать дверь, и вы указываете на одну из дверей. Далее ведущий решает открыть одну из двух оставшихся дверей. Он выбирает одну из них (допустим, подбросив монетку), открывает ее, и за ней оказывается овца. Тогда ведущий предлагает вам поменять ваш выбор. Вопрос: основываясь на доступной вам информации, имеет ли смысл менять выбор.
Ответ: совершенно не важно, поменяете ли вы выбор, Феррари равновероятно спрятана за одной из двух закрытых дверей.
Если вы согласны с этим ответом, то статья вам покажется не очень интересной. А если не согласны, то может понравиться.
Читать полностью »
Лекции от Яндекса для тех, кто хочет провести каникулы с пользой. Дискретный анализ и теория вероятностей
2014-01-04 в 10:49, admin, рубрики: Блог компании Яндекс, математика, теория вероятностей, Учебный процесс в IT, школа анализа данных, Яндекс.Почта, метки: теория вероятностей, школа анализа данных, Яндекс.ПочтаДля тех, кому одного курса на праздники мало и кто хочет больше, продолжаем нашу серию курсов от Школы анализа данных Яндекса. Сегодня подошла очередь курса «Дискретный анализ и теория вероятностей» – даже более фундаментального, чем предыдущий. Но без него нельзя представить ещё большую часть современной обработки данных.
В рамках курса рассматриваются основные понятия и методы комбинаторного, дискретного и асимптотического анализа, теории вероятностей, статистики и на примере решения классических задач демонстрируется их применение.
Читает курс Андрей Райгородский. Доктор физико-математических наук. Профессор кафедры математической статистики и случайных процессов механико-математического факультета МГУ им. М. В. Ломоносова. Заведующий кафедрой Дискретной математики ФИВТ МФТИ. Профессор и научный руководитель бакалавриата кафедры «Анализ данных» факультета инноваций и высоких технологий МФТИ. Руководитель отдела теоретических и прикладных исследований компании «Яндекс». (Ещё больше можно узнать в статье о нём на Википедии).
Парадокс Монти Холла и Excel
2013-11-12 в 4:23, admin, рубрики: математика, парадокс монти холла, теория вероятностей, метки: парадокс монти холла, теория вероятностейНесчастны те люди, кто не умеет программировать хотя бы на уровне формул Excel! Например, им всегда будет казаться, что парадоксы теории вероятностей – это причуды математиков, неспособных понимать реальную жизнь. Между тем, теория вероятностей как раз-таки моделирует реальные процессы, в то время как человеческая мысль часто не может в полном объеме осознать происходящее.
Возьмем парадокс Монти Холла, приведу здесь его формулировку из русской Википедии:
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Читать полностью »
Вероятностные модели: борьба с циклами и вариационные приближения
2013-08-02 в 16:03, admin, рубрики: data mining, байесовские сети, Блог компании Surfingbird, искусственный интеллект, математика, математическое моделирование, теория вероятностей, метки: data mining, байесовские сети, математика, математическое моделирование, теория вероятностейВ четвёртой серии цикла о графических вероятностных моделях (часть 1, часть 2, часть 3) мы продолжим разговор о том, как справляться со сложными фактор-графами. В прошлый раз мы изучили алгоритм передачи сообщений, который, правда, работает только в тех случаях, когда фактор-граф представляет собой дерево, и в каждом узле можно без проблем пересчитать распределения грубой силой. Что делать в по-настоящему интересных случаях, когда в графе есть большие содержательные циклы, мы начнём обсуждать сегодня – поговорим о паре относительно простых методов и обсудим очень мощный, но непростой в использовании инструмент – вариационные приближения.
Вероятностные модели: искусство расставлять скобки
2013-07-04 в 17:20, admin, рубрики: data mining, байесовские сети, Блог компании Surfingbird, искусственный интеллект, математика, математическое моделирование, теория вероятностей, метки: data mining, байесовские сети, математика, математическое моделирование, теория вероятностейПосле большого перерыва продолжаем цикл о графических вероятностных моделях (часть 1, часть 2). Сегодня мы наконец-то от постановок задач перейдём к алгоритмам; поговорим мы о самом простом, но часто полезном алгоритме вывода на фактор-графах – алгоритме передачи сообщений. Или, как его ещё можно назвать, алгоритме правильной расстановки скобок.
Тщетные попытки победить лотерею
2013-05-14 в 9:35, admin, рубрики: алгоритм, Алгоритмы, игра, искусственный интеллект, лотерея, математика, теория вероятностей, метки: алгоритм, игра, лотерея, теория вероятностей Представим воображаемый хитрого дядю, который хочет обмануть и заработать деньги на «лопухах». Назовем его Геннадий Обмануев.
В самый обычный вторник, Геннадию Обмануеву вдруг пришла гениальная идея: создать лотерею, в которой каждый игрок может сам указывать свой шанс на победу и, следовательно, множитель выигрыша и играть на выставленных им правилах! Для того, чтобы всегда оставаться в плюсе, Геннадий в конце каждой удачной игры берет символическую плату в 5% от выигрыша.
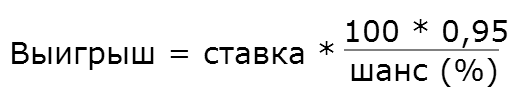
*если кратко об игре
Как и в случае с казино, чем дольше игрок играет в такую игру — тем более вероятно, что он, в конце концов, проиграет. Но неужели нельзя обмануть хитрого дядю, придумав чудесную тактику, благодаря которой можно увеличить свои шансы на победу?
Читать полностью »
Разбор «лохотрона» на игральных картах
2013-05-11 в 10:17, admin, рубрики: Алгоритмы, карты, лохотрон, математика, развод, теория вероятностей, метки: карты, лохотрон, развод, теория вероятностейВместо вступления
В стандартной колоде для покера 54 карты. Без двух джокеров, которые не участвуют в игре, выходит 52 карты. Если вы хорошенько перемешаете колоду, то, возможно, создадите уникальную комбинацию из карт, которую никогда никто не создавал до вас. Потому что различных вариантов расположений 52 карт равно: 

Что-то мне подсказывает, что комбинация на изображении не так уникальна.
Теперь к теме
Недавно я узнал про метод «барного развода» на игральных картах, благодаря которому «умные дяди» выигрывают приличные суммы. Суть такова:
«Разводчик» приходит в бар и некоторое время болтает с окружающими, чаще всего присоединяется к большим компаниям молодых людей. Он пытается влиться в компанию и стать «своим» среди окружающих. После того, как он заслужил некоторое доверие и к нему привыкли, разводчик выбирает самого вспыльчивого и разводит его на спор:
Я слышал, что у [блондинов/низких людей/тех, кто носит кепки/любой подходящий вариант] интуиция просто отстой! Вот спорим, что ты не сможешь угадать (в этот момент разводчик достает колоду карт) цвет каждой следующей карты? Можешь перетасовать колоду, как захочешь! За каждую угаданную карту плачу по тысяче рублей! А если не угадаешь, то ты даешь мне один рубль, потом докидываешь до двух, до четырех рублей и дальше, ну ты понял? И чтобы было честно — остановить игру может лишь тот, кто проигрывает. Идет?
Большинство читателей уже поняли схему и с улыбкой прикидывают сумму, которую может выиграть разводчик.
Мне стало интересно, до каких пор игрок выигрывает и как нужно действовать, чтобы увеличить шансы на выигрыш (лучший способ — отказаться от игры!). Естественно, правило про остановку игры я не учитываю, с ним выиграть невозможно.
Читать полностью »
Теория вероятностей и антропогенный фактор
2013-05-06 в 7:46, admin, рубрики: математика, теория вероятностей, метки: математика, теория вероятностей 
Введение
Среди людей бытует мнение, что человек, поступивший на математический факультет, обязательно выйдет оттуда учителем математики. Это не я придумал, это по опыту, ибо довольно большое количество не очень образованных людей спрашивало, куда я собираюсь идти работать после окончания ВУЗа. Разумеется, найти можно и куда более обширные области применения своих знаний. Одна из них связана с теорией вероятности. Я не хочу вникать в сложные подробности предмета, т.к. люди, не имеющие нужной математической базы, скорее всего запутаются. Но и говорить совсем ни о чем не хочется. Поэтому я хочу написать про связь человека и этой самой теории вероятностей, причем на простом, понятном любому языке. Если интересно — прошу под кат.
Читать полностью »
Вероятностные модели: примеры и картинки
2013-04-25 в 6:26, admin, рубрики: data mining, байесовские сети, Блог компании Surfingbird, искусственный интеллект, математика, математическое моделирование, теория вероятностей, метки: data mining, байесовские сети, математика, математическое моделирование, теория вероятностейСегодня – вторая серия цикла, начатого в прошлый раз; тогда мы поговорили о направленных графических вероятностных моделях, нарисовали главные картинки этой науки и обсудили, каким зависимостям и независимостям они соответствуют. Сегодня – ряд иллюстраций к материалу прошлого раза; мы обсудим несколько важных и интересных моделей, нарисуем соответствующие им картинки и увидим, каким факторизациям совместного распределения всех переменных они соответствуют.




