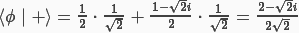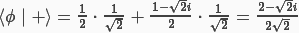Сего дня я хотел бы предложить своим читателям небольшую заметку о том, как при помощи языка Haskell разработать модуль для выполнения символьных вычислений. В этой заметке будет описано только самое начало — как подступиться к задаче, какие типы данных использовать, как привязать к решению задачи мощную систему вывода типов языка Haskell. При помощи разработанных программных сущностей мы попробуем решить одну простенькую задачу по квантовой механике или даже, скорее, по линейной алгебре (она взята из первого задания курса «Quantum Mechanics and Quantum Computation» на Coursera — задача № 11). При этом мы посмотрим, как последовательное написание функций для выполнения символьных вычислений позволяет всё ближе и ближе подойти к правильному решению.
Вот условие задачи:
Let |ϕ> = ½ |0> + (1 + √2 i)/2 |1> be the state of a qubit. What is the inner product of |ϕ> and |+>?
Другими словами, необходимо найти скалярное произведение двух векторов, которые представляют кубиты |ϕ> и |+>, причём первый кубит задан в базисе (|0>, |1>), а то, как в этом же базисе раскладывается второй кубит, надо помнить :).
Для решения задачи мы будем пользоваться соглашением о скалярном произведении комплекснозначных векторов, принятом в физике — для этого используется так называемая нотация Дирака. Это значит, что при произведении компонентов векторов, для первого вектора необходимо взять сопряжённые комплексные числа. Но это частность. В общем же нашей задачей является написание общего модуля для решения символьных выражений. Почему символьных? Потому что ответ требуется примерно в таком же виде, в каком задано условие — в виде дробей, невычисленных квадратных корней и т. д.
Читать полностью »
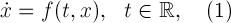
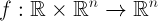представляет собой сумму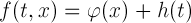
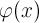и тригонометрического полинома 
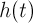, являющегося 
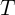-периодической векторной функцией.