Метка «периодические решения»

в 19:08, , рубрики: дифференциальные уравнения, математика, периодические решения, символьные вычисления, метки: , ,

В прикладной математике иногда возникает задача построения периодических решений нормальной системы обыкновенных дифференциальных уравнений вида

image

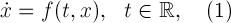
где функция 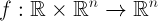image представляет собой сумму

image

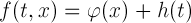
многомерного многочлена 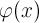image и тригонометрического полинома 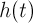image, являющегося 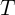image-периодической векторной функцией.

Многие из теорем существования периодических решений системы (1) используют тот фундаментальный факт, что такие решения полностью определяются неподвижными точками оператора сдвига по траекториям системы. Однако использование данных теорем для непосредственного нахождения нужного периодического решения, скорее всего, не представляется возможным.
Читать полностью »

в 20:35, , рубрики: дифференциальные уравнения, интегратор, математика, периодические решения, численные методы, метки: , , ,

1. Об аттракторе Лоренца

image

Эдвард Нортон Лоренц (1917 – 2008) является основателем теории хаоса, очень популярной в науке на сегодняшний день. Он учился в колледже Дартмут штата Нью-Гемпшир США и Гарвардском университете в Кембридже. Во время Второй мировой войны служил метеорологом в авиационном корпусе армии США, потом до конца своих дней работал профессором в Массачусетском технологическом институте.

В 1963 году в журнале «Journal of the Atmospheric Sciences» вышла его статья «Deterministic Nonperiodic Flow» (русский перевод: Лоренц Э. Детерминированное непериодическое течение // Странные аттракторы. — М.: Мир, 1981, с. 88-117), заложившая не только основы теории хаоса, но и изменившая представления о моделировании погодных явлений. В этой работе из системы уравнений Навье-Стокса впервые была получена нелинейная автономная система обыкновенных дифференциальных уравнений третьего порядка (динамическая система), описывающая движение воздушных потоков в плоском слое жидкости постоянной толщины при разложении скорости течения и температуры в двойные ряды Фурье с последующем усечением до первых-вторых гармоник:Читать полностью »

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js