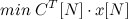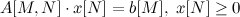Требуемые знания: знакомство с методами линейного программирования, методы решения транспортной задачи(особенно метод потенциалов).
Год назад, на третьем.jpg "Транспортная задача с партийными перевозками(«с трейлерами»)")
курсе в качестве одной из лабораторных работ по курсу «Методы оптимизации» мне задали реализовать решение транспортной задачи, но с одним небольшим условием: перевозки происходят партиями. Это значит, что теперь, в отличие от классической постановки, оплачивается перевозка партии товаров (e.g. 10 штук), и, даже если Вам надо перевезти 11 штук, Вы заплатите за две партии(в один трейлер 11 штук не влезут). Казалось бы, мелкое дополнение, однако как теперь решать задачу, да хотя бы как её формализовать? Как студенту кафедры прикладной математики, мне было не привыкать, что великий google.ru чего-то не знает, но каково же было моё удивление, когда ни его старший брат — англоязычный google, ни тьма перебранных мной книг по теории оптимизации не смогли ответить на этот вопрос.
Читать полностью »
