Задачи на разрезание — это та область математики, где, как говорится, мамонт не валялся. Множество частных задач, но практически нет общей теории. Помимо всем известной теоремы Бойяи-Гервина, других фундаментальных результатов в этой области практически нет. Неопределённость — вечный спутник задач на разрезание. Мы можем, например, разрезать правильный пятиугольник на шесть частей, из которых можно сложить квадрат; однако мы не можем доказать, что пяти частей для этого было бы недостаточно.
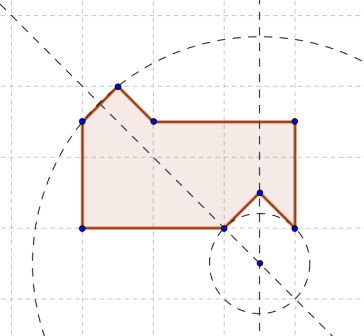
С помощью хитрой эвристики, воображения и поллитры нам порой удаётся найти конкретное решение, но, как правило, мы не обладаем подходящим инструментарием, чтобы доказать минимальность этого решения или же его несуществование (последнее, разумеется, относится к случаю, когда мы решение не нашли). Это печально и несправедливо. И как-то раз я взял чистую тетрадку и решил восстановить справедливость в масштабах одной конкретной задачи: разрезания плоской фигуры на две равных (конгруэнтных) части. В рамках этого цикла статей (их, кстати, будет три) мы с вами, камрады, рассмотрим вот этот забавный многоугольник, изображённый ниже, и попытаемся беспристрастно разобраться, можно ли разрезать его на две равных фигуры, или же таки нет.