Комбинаторика в старших классах школы, как правило, ограничивается текстовыми задачами, в которых нужно применить одну из трёх известных формул — для числа сочетаний, перестановок или размещений. В институтских курсах по дискретной математике рассказывают и о более сложных комбинаторных объектах — скобочных последовательностях, деревьях, графах… При этом, как правило, ставят задачу вычислить количество объектов данного типа для некоторого параметра n, например количество деревьев на n вершинах. Узнав количество объектов для фиксированного n, можно задаться и более сложным вопросом: как все эти объекты за разумное время предъявить? Алгоритмы, решающие подобного рода задачи, называются алгоритмами комбинаторной генерации. Таким алгоритмам, например, посвящена первая глава четвёртого тома «Искусства Программирования» Дональда Кнута. Кнут очень подробно рассматривает алгоритмы генерации всех кортежей, разбиений числа, деревьев и других структур. Придумать какой-нибудь алгоритм, работающий умеренно быстро, для каждой из этих задач несложно, но с дальнейшей оптимизацией могут возникнуть серьёзные проблемы.
В процессе написания магистерской диссертации, защищённой в Академическом Университете, мне потребовалось изучить и применить один из алгоритмов комбинаторной генерации, подходящий для особого класса задач. Это генерация структур, на которых дополнительно введено некоторое отношение эквивалентности. Чтобы было понятно, о чём идёт речь, я приведу простой пример. Давайте попробуем сгенерировать все триангуляции шестиугольника. Получится что-нибудь такое:
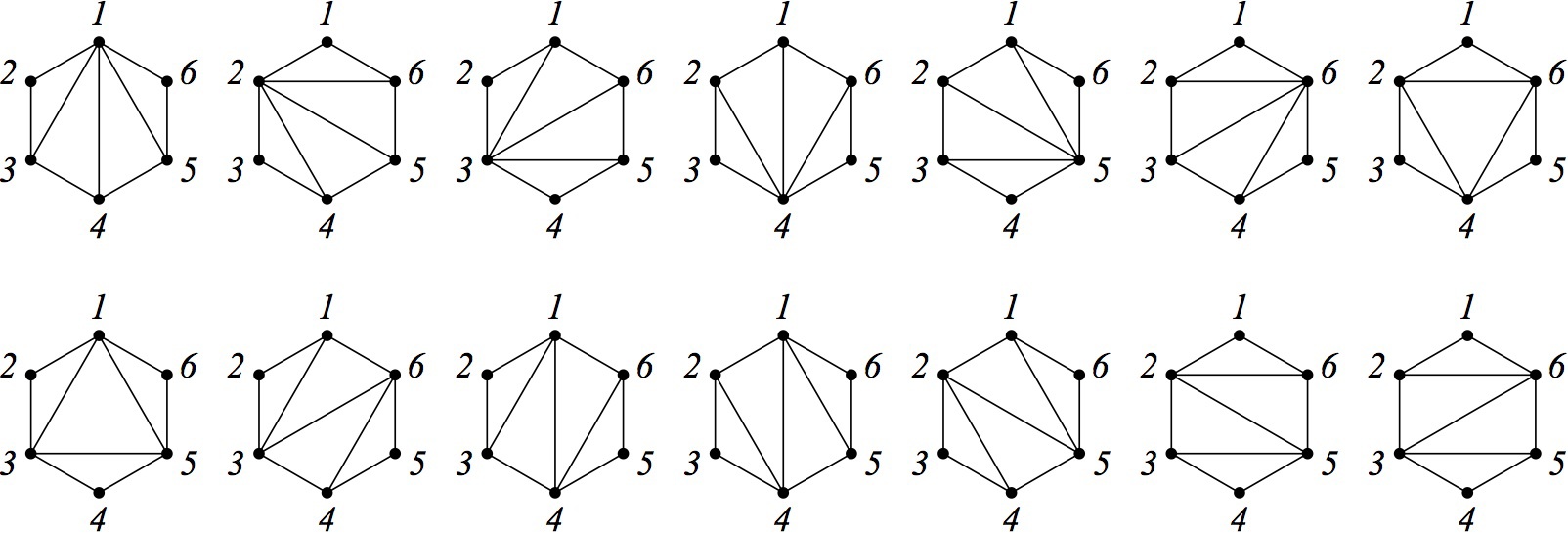
Написать алгоритм, который вернёт все такие триангуляции, довольно несложно. Например, сгодится такая процедура: фиксируем какое-нибудь ребро (пусть это будет ребро 1-6), после чего в цикле перебираем вершины, не являющиеся его концами. На текущей вершине и фиксированном ребре строим треугольник, а оставшиеся после этого две области триангулируем рекурсивно. Если присмотреться к получающимся в результате работы этого алгоритма триангуляциям, то можно заметить, что многие из них почти одинаковы и отличаются лишь тем, как расставлены пометки (номера) вершин. Поэтому, полезно было бы придумать алгоритм, который будет генерировать так называемые непомеченные триангуляции — те, что изображены на следующем рисунке:
Читать полностью »





