Это седьмая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре:
- Теория категорий для программистов: предисловие
- Категория: суть композиции
- Типы и функции
- Категории, большие и малые
- Категории Клейсли
- Произведения и копроизведения
- Простые алгебраические типы данных
Функторы
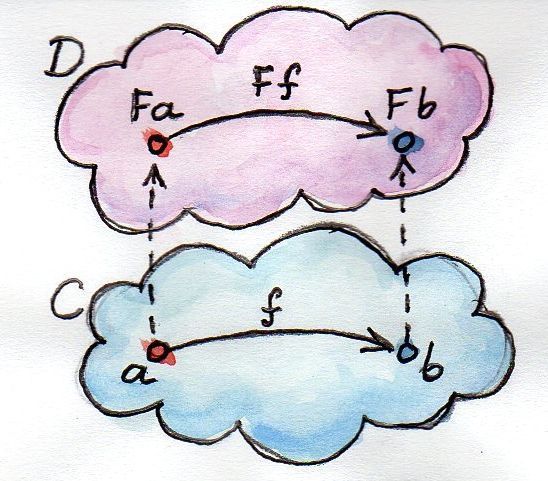
За понятием функтора стоит очень простая, но мощная идея (как бы заезжено это ни прозвучало). Просто теория категорий полна простых и мощных идей. Функтор есть отображение между категориями. Пусть даны две категории C и D, а функтор F отображает объекты из C в объекты из D — это функция над объектами. Если a — это объект из C, то будем обозначать его образ из D как F a (без скобок). Но ведь категория — это не только объекты, но еще и соединяющие их морфизмы. Функтор также отображает и морфизмы — это функция над морфизмами. Но морфизмы отображаются не как попало, а так, чтобы сохранять связи. А именно, если морфизм f из C связывает объект a с объектом b,
f :: a -> bто образ f в D, F f, связывает образ a с образом b:
F f :: F a -> F b(Надеемся, что такая смесь математических обозначений и синтаксиса Haskell понятна читателю. Мы не будем писать скобки, применяя функторы к объектам или морфизмам.)