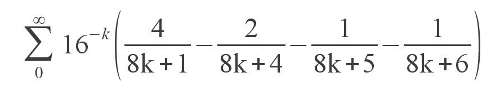Метка «Алгоритмы» - 8

в 22:16, , рубрики: c++, Алгоритмы, интересный код, Программирование, метки: ,

Преподаватель из Стэнфордского университета Кейт Шварц (Keith Schwarz) уже несколько лет пополняет свой архив интересного кода — образцы самых лучших алгоритмов и структур данных, когда-либо изобретённых человечеством (Шварц весьма амбициозно оценивает свою коллекцию).

Примеры на сайте преимущественно закодированы в C++, поскольку этот язык лучше всего подходит для описания алгоритмов. Структуры данных реализованы на Java.

Кейт Шварц дает разрешение использовать свой код всем желающим без всяких ограничений.
Читать полностью »

в 12:07, , рубрики: Алгоритмы, динамическое программирование, Морской бой, метки: , ,

Раз уж неделя «Морского боя» на Хабре продолжается, добавлю и я свои два цента.
При попытке найти оптимальную стратегию для игры за компьютер довольно быстро приходим к такому приближению:

Допустим, что состояние некоторых клеток нам уже известно, и мы хотим сделать ход, максимально приближающий нас к победе. В таком случае имеет смысл выбирать клетку, которая занята кораблём противника в наибольшем числе возможных размещений кораблей, не противоречащих имеющейся информации

В самом деле. Если возможная конфигурация только одна, то мы заканчиваем игру за один ход, расстреливая его корабли по очереди (ведь конфигурация нам известна!) Если же конфигураций больше, то нам нужно уменьшить их число как можно сильнее, тем самым увеличив имеющееся у нас количество информации. Если мы попадём в корабль, то ничего не потеряем (ведь ход остаётся у нас!), а если промахнёмся — то число оставшихся комбинаций будет минимальным из возможных после этого хода.

Снова «Морской бой». Считаем число возможных расположений кораблей
Понятно, что это только приближение к отпимальной стратегии. Если противник будет знать о нашем плане, он постарается разместить корабли так, чтобы они не попадали в те клетки, куда мы будем стрелять в начале игры. Правда, ему это поможет мало — мы всё равно в конце концом зажмём его в угол — но возможно, что определённая гибкость нам не помешала бы. Кроме того, не исключено, что продуманная серия ходов, первый из которых не является оптимальным, привела бы к лучшему результату. Но не будем пока усложнять и без того сложную задачу, а попытаемся просчитать все конфигурации и построить карту вероятности заполнения поля.

На первый взгляд, задача кажется неподъёмной. Число конфигураций представляется порядка 1020 (на самом деле их несколько меньше — ближе к 1015), так что на полный перебор времени уйдёт слишком много. Перебирать раскраски поля и оставлять только допустимые — не лучше: всё равно нам каждую комбинацию придётся просмотреть.

Что же ещё попробовать? Любой олимпиадник тут же ответит — динамическое программирование. Но как его организовать?

Читать полностью »

в 21:42, , рубрики: java, Алгоритмы, градиент, обработка изображений, Программирование, метки: , , , ,

А давайте я вам расскажу про градиенты!
скрин финального результата

В этой статье я рассказываю о том, как я изобрел свой личный велосипед, рисующий градиент практически как в фотошопе. Сразу предупреждаю, алгоритм ужасно медленный и неоптимизированный. Оптимизацией и рассмотрением какого-нибудь популярного алгоритма градиента я собираюсь заняться во второй части статьи

Зачем?

Как-то захотелось мне реализовать программную отрисовку градиентов, максимально похожих на фотошоповские. Никакой конкретной цели у меня не было, так, интересная задачка на вечер. В качестве языка была выбрана Java. Важной идеей было то, что я хотел написать этот алгоритм именно своими силами, не подглядывая в чужие алгоритмы.
Читать полностью »

в 14:45, , рубрики: Алгоритмы, Дракон, ненормальное программирование, обучение, Учебный процесс в IT, метки: , ,

Википедия о Драконе.
Дракон иногда называют правильными блок-схемами. Но в первую очередь он отлично подходит для записи алгоритмов.
Внутри НПЦ АП (Научно-производственный центр автоматики и приборостроения) Дракон используется с помощью закрытой технологии ГРАФИТ-ФЛОКС. За рамками НПЦ АП есть открытые технологии, на которых можно писать реальные программы на гибридных языках Дракон-Си, Дракон-Delphi, Дракон-1С, Дракон-ASM, Дракон-Erlang и т.д.

Доклад читает Владимир Паронджаров в Институте проблем управления РАН им.Пилюгина.

Текстовая версия данного доклада
Читать полностью »

в 11:03, , рубрики: Алгоритмы, математика, метки:

В математике сети дорог (автомобильных и не только) представляются взвешенным графом. Населенные пункты (или перекрестки) — это вершины графа, ребра — дороги, веса ребер — расстояния по этим дорогам.

Для взвешенных графов предлагается множество алгоритмов. Например, популярный алгоритм Дейкстры для поиска кратчайшего пути от одной вершины до другой. У всех этих алгоритмов есть общая принципиальная (для математики) особенность — они универсальны, т.е. могут успешно применяться для графов любой конструкции. В частности, для каждого алгоритма известна его сложность – она примерно соответствует увеличению времени выполнения алгоритма в зависимости от числа вершин графа. Все это подробно можно прочитать, например, в википедии.

Вернемся к практическим задачам. Дороги представляются взвешенным графом, но дороги — это не любой граф. Другими словами, нельзя из любого графа построить дорожную сеть. В отличие от виртуального графа как математической абстракции, дороги строятся людьми из реальных материалов и стоят довольно больших денег. Поэтому они прокладываются не как попало, а по определенным экономическим и практическим правилам.

Мы не знаем эти правила, однако, работая с дорожными сетями, вполне можно использовать алгоритмы, которые эффективны для графов дорог, хотя и не подходят для графов в универсальном или математическом смысле. Рассмотрим здесь два таких алгоритма.
Читать полностью »

в 5:38, , рубрики: data mining, Алгоритмы, статистика, метки: , ,

Нам нужно реализовать детектор лжи, который по подрагиванию рук человека, определяет, говорит он правду или нет. Допустим, когда человек лжет, руки трясутся чуть больше. Сигнал может быть таким:

Исходный сигнал

Интересный метод, описан в статье «A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition» L.R. Rabiner, которая вводит модель скрытой цепи Маркова и описывает три ценных алгоритма: The Forward-Backward Procedure, Viterbi Algorithm и Baum-Welch reestimation. Несмотря на то, что эти алгоритмы представляют интерес только в совокупности, для большего понимания описывать их лучше по отдельности.
Читать полностью »

в 18:39, , рубрики: c++, Алгоритмы, оптимизация программ, Программирование, С++, метки: , , ,

При оптимизации времени выполнения алгоритма, использующего LDPC декодер, профайлер привел к функции, вычисляющей следующее значение:
image
где a и b — целые числа. Количество вызовов шло на миллионы, а реализация ее была достаточно Читать полностью »

в 16:32, , рубрики: Алгоритмы, математика, число пи, метки: , ,

С недавних пор существует элегантная формула для вычисления числа Пи, которую в 1995 году впервые опубликовали Дэвид Бэйли, Питер Борвайн и Саймон Плафф:
image

Казалось бы: что в ней особенного — формул для вычисления Пи великое множество: от школьного метода Монте-Карло до труднопостижимого интеграла Пуассона и формулы Франсуа Виета из позднего Средневековья. Но именно на эту формулу стоит обратить особое внимание — она позволяет вычислить n-й знак числа пи без нахождения предыдущих. За информацией о том, как это работает, а также за готовым кодом на языке C, вычисляющим 1 000 000-ый знак, прошу под хабракат.
Читать полностью »

в 8:17, , рубрики: Алгоритмы, Песочница, метки: , ,

Доброго времени суток всем читающим. Сначала изложу предысторию данного вопроса. Началось все с того что знакомый попросил меня по работе помочь ему сделать приложение (WinForm на C#), которая бы алгоритмом CART создавала бинарное дерево решений, исходя из статистических данных находящихся в таблице на форме. Суть в том, чтобы делить исходную таблицу на 2 части по вычисляемым критериям. Для того чтобы поделить исходную таблицу, мы должны найти среднее по каждому из столбцов:
Читать полностью »

в 14:40, , рубрики: Алгоритмы, математика, математические формулы, Песочница, метки: , ,

Доброго времени суток!
Этот пост для тех, кто хочет научиться строить Фундаментальную Матрицу решений Системы Линейных Дифференциальных Уравнений, но боится.

Предыстория

Если немного погуглить на эту тему, то можно найти достаточное количество статей, большинство из которых описывают построение Фундаментальной матрицы через Жордановы формы.
Мне кажется, что это достаточно сложно понять вот так вот сразу, а тем более воплотить в жизнь.
Читать полностью »

1...789...16
Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js