Введение
В данной статье пойдет речь о методе распознавания рукописного ввода путем математического анализа всех точек плоскости и перебора всех возможных комбинаций с целью отыскать наиболее лучшее наложение контрольных точек на ранее описанные фигуры. Поясню.
Рукописный ввод — это рисование мыслимым «пером» определенной фигуры. Рисование в компьютерных системах — это сохранение в графической памяти информации обо всех пикселях графического контекста. «Точка на плоскости» в математике — понятие абстрактное. В компьютерной же графике за этим понятием скрывается «пиксель». Данный алгоритм распознавания будет анализировать предоставленный ему набор точек( пикселей ) и пытаться в нем отыскать наиболее возможную и похожую фигуру. Фигура, в свою очередь, это каркас, содержащий лишь основные( контрольные ) точки, делающие фигуру уникальной.
Матчасть
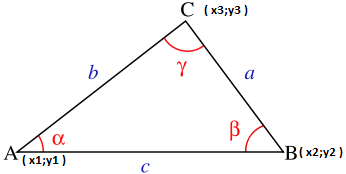
Вообще говоря, сердце алгоритма — всем известная со времен школы Теорема Косинусов, являющаяся обобщенной теоремой Пифагора. Зная координаты трех точек плоскости и их порядок «появления» на ней, мы можем с легкостью определить угол, описанный этими точками( Вершина угла — вторая по счету точка ):
A( x1;y1 )
B( x2;y2 )
C( x3;y3 )расстояния между точками находятся по теореме Пифагора
a^ = b^ + c^ — 2*b*c*cos(ALPHA)
cos(BETA) = (b^+c^-a^) / 2*b*c
Зная косинус, величину угла легко можно вычислить.
Среди набора точек, которые подаются на вход алгоритма, необходимо «подставить» точки во всевозможные каркасы фигур( о них выше ) и выбрать наилучшее решение среди найденных. Делается это следующим образом:
- Мы берем первую и последнюю точки каркасов фигур. Уже две есть, осталось отыскать третью ( для нахождения величины угла ).
- Поиск третьей осуществляется перебором все последующих точек после первой. Решение включать точку в предполагаемый каркас фигуры принимается на основе двух анализов:
- Попытка подставить точку в угол( в качестве третьей, заключительной ) и проверить его на соответствие величине того же угла в каркасе реальной фигуры.
- Проверить отношение сторон получившегося угла с тем же отношением сторон угла в каркасе реальной фигуры.
Если эти два условия выполняются, то алгоритм принимает решение о включении точки из набора точек в мыслимый каркас( при этом увеличиваем величину похожести на текущую анализируемую фигуру ).
Если, допустим, у нас есть несколько анализируемых каркасов, например, «8» и «6». И результат алгоритма распознавания: «8»-80%, «6» — 90%, то решение принимается в пользу той фигуры, в каркасе которой присутствует больше контрольных точек, т.е в пользу восьмерки.
Процент сходства набора точек с точками в каркасе высчитывается просто: суммируются все точки, которые сошлись с теми же точками в каркасе и находится отношение. Допустим, если в каркасе N контрольных точек, а у нас сошлось M, то процент сходства —
M / N * 100

.jpg)
