Сегментация изображений является задачей разбиения цифрового изображения на одну или несколько областей, представляющих интерес. Это фундаментальная проблема в области компьютерного зрения, которая решается многими различными способами, каждый из которых обладает своими преимуществами и недостатками.
В этой статье я кратко рассмотрю понятие метода фиксации уровня и неявно заданных динамических поверхностей (level set method). Также рассмотрю роль этого метода в бинарной сегментации с введением и определением математических конструкций, таких как SDT (Signed Distance Transforms), маркированной карты расстояний.
 Слева — исходное изображение, справа — сегментированное
Слева — исходное изображение, справа — сегментированное
Зачем все это?
В различных отраслях часто возникает потребность получения сегментированных изображений. Например, в медицине, где существует интерес к получению цифровых 3D моделей органов для дальнейшего анализа. Также сегментация применяется в распознавании лиц, машинном зрении и т.д.
Сегментация изображений является особенно трудной задачей по нескольким причинам. Во-первых, в настоящее время не существует универсальных алгоритмов сегментации, поэтому необходимо создавать специальные алгоритмы, параметры которых подбираются пользователем, исходя из конкретных условий. Во-вторых, искажения изображения, такие как шум, неоднородность и т.д., очень трудно учесть в алгоритмах сегментации без участия пользователя.
Со второй проблемой обычно борются применением различного рода фильтров. Эта технология отлично описана здесь.
Я столкнулся с задачей сегментации изображений в нефтегазовой отрасли. Первоначально мы имели плоские изображения керна (как на рисунке выше). Получив сегментированное изображение, мы можем провести интерполяцию границ. Проведя данную операцию для всех изображений, мы можем получить математическую модель нашего образца горной породы, с которой можно работать и на которой, например, можно задавать течение флюидов (если рассматривать нашу модель как модель механики сплошной среды).
Метод фиксации уровня
Этот метод был введен американскими математиками Стэнли Ошером и Джеймсом Сетьяном в 1980-е годы. Он стал популярным во многих дисциплинах, таких как компьютерная графика, обработка изображений, вычислительная геометрия, оптимизация, вычислительная гидродинамика и вычислительная биофизика.
Метод фиксации уровня неявно преобразует контур (в двух измерениях) или поверхность (в трех измерениях), используя функцию более высокой размерности, называемую функцией фиксации уровня $inline$φ(x,t)$inline$. Преобразованный контур или поверхность можно получить как кривую $inline$Gamma(x,t)={φ(x,t)=0}$inline$.
Преимущество использования этого метода состоит в том, что топологические изменения, такие как слияние и разделение контура или поверхности, решаются неявно, как показано ниже на рисунке.
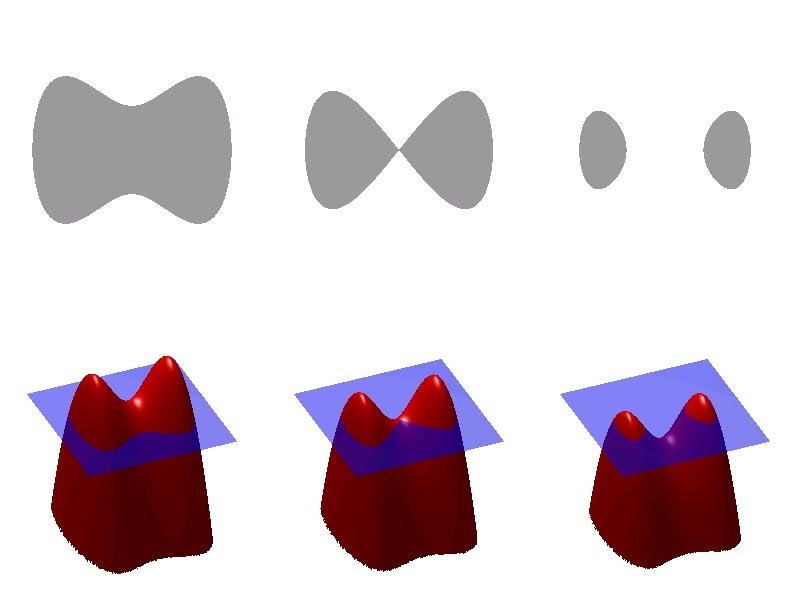
Можно видеть взаимосвязь между функцией фиксации уровня (снизу) и контуром (сверху). Видно, что изменение поверхности разбивает контур.
Уравнение модификации уровня
Задание контура или поверхности определяется уравнением модификации уровня. Численное решение этого дифференциального уравнения в частных производных мы получаем путем обновления $inline$φ $inline$ для каждого временного слоя. Общий вид уравнения модификации уровня имеет вид:
$$display$$ frac{∂φ}{∂t} = -F|∇φ| qquad(1)$$display$$
где:
$inline$| · |$inline$ — евклидова норма,
$inline$φ$inline$ — функция фиксации уровня,
$inline$t$inline$ — время,
$inline$F $inline$ — коэффициент скорости.
Это уравнение в частных производных очень похоже на гиперболическое. Но из-за того, что в правой части уравнения помимо производной по пространству также есть производная по времени оно, строго говоря, таким не является.
При определенном задании вида вектора $inline$F $inline$ с точностью до параметров, мы можем направлять линию уровня на разные области или формы.
Для приложений в сегментировании будем задавать $inline$F $inline$ так:
$$display$$F = αD(I)+(1-α)∇cdotfrac{∇φ}{|∇φ|} qquad(2)$$display$$
где:
$inline$D(I)$inline$ — функция данных, склоняющая решения к желаемому сегментированию,
$inline$I$inline$ — значение интенсивности пиксела,
$inline$∇cdotfrac{∇φ}{|∇φ|}$inline$ — средний член кривизны функции $inline$φ$inline$, который будет сохранять эту функцию гладкой,
$inline$alpha$inline$ — весовой параметр.
Функция данных $inline$D(I) $inline$ действует как главная «сила», которая управляет сегментацией. Делая $inline$D $inline$ положительным в желаемых областях или отрицательным в не желаемых, модель будет стремиться к желаемому сегментированию. Вот простая функция данных:
$$display$$ D(I)= ε-|I-T| qquad(3) $$display$$
Ее работа приведена ниже на рисунке:
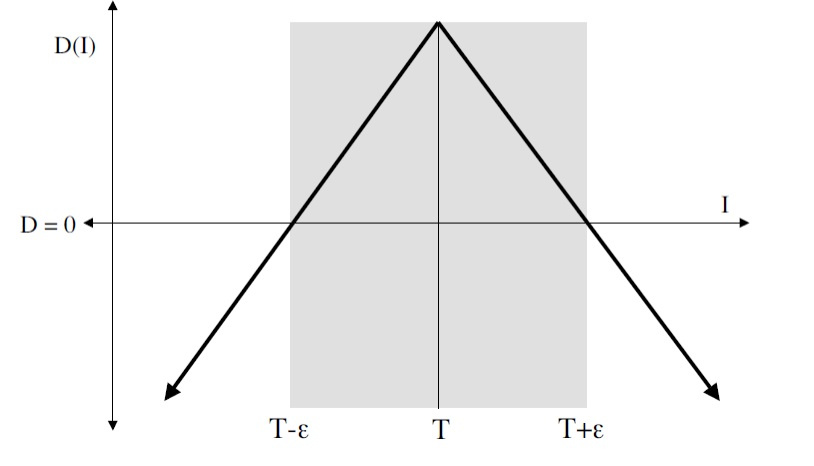
То есть если значение пиксела попадает в интервал $inline$(T - ε, T+ ε)$inline$, то диапазон модели будет расширяться, иначе — сужаться.
Поэтому три пользовательских параметра, которые необходимо указать для сегментации, — это $inline$T,$inline$ ε и $inline$alpha$inline$.
Например, если нам нужно выделить на изображении объекты с низким уровнем яркости (черные области), то $inline$T$inline$ выбирается равным нулю.
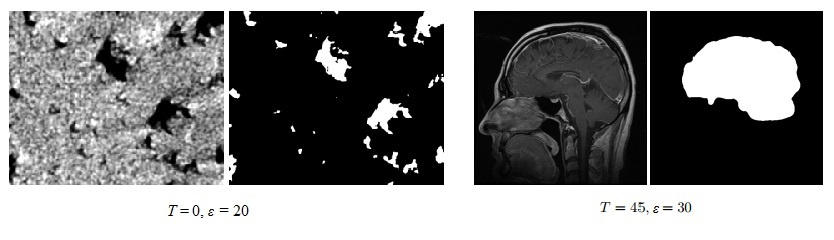
Слева выделяем черные области, справа — желаемая область имеет более большую яркость, поэтому выбираем $inline$T = 45$inline$
Также требуется задание начальной маски $inline$m$inline$. От того, какой мы ее выберем, будет зависеть начальное приближение $inline$φ$inline$. Для этого введем понятие маркированной карты расстояний
Маркированная карта расстояний (Signed Distance Transforms)
Карта расстояний – это матрица, которая имеет такую же размерность, что и наше изображение. Строится она таким образом: для каждого пиксела нашего изображения высчитывается значение, равное минимальному расстоянию от этого пиксела до ближайшего пиксела на границе объекта (ов). Математическое определение функции расстояния $inline$d: R^3 to R $inline$ для множества S:
$$display$$d(r,S)=min|r-S| qquad для всех qquad r∈R^3$$display$$
Маркированная карта расстояний — это матрица, имеющая положительный знак перед значениями пикселов, которые находятся вне объекта, и отрицательный для тех, которые внутри него. Это соглашение о знаке, которое будет выполняться при реализации, однако можно было бы использовать и противоположную конвенцию знака. Следует отметить, что значения ячеек зависят от выбранной метрики: некоторые общие метрики расстояния — это евклидово расстояние, расстояние Чебышёва ( Chebyshev distance, chessboard distance) и расстояние городских кварталов (Taxicab geometry, city block distance, Manhattan distance).
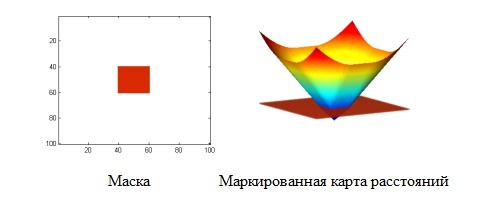
Слева выбранная нами начальная маска. Это объект любой формы, находящийся внутри интересующего нас объекта. Чаще всего это прямоугольник, потому что его довольно просто задать. После определенного количества итераций функция справа (функция модификации уровня) меняется таким образом, чтобы ее пересечение с нулевой плоскостью давало интересующую нас кривую
Дискретизация
Уравнение (1), уравнение уровня, должно быть дискретизировано для последовательного или параллельного вычисления. Это делается с использованием разностной схемы с разностями против потока (upwind).
Метод первого порядка точности для дискретизации по времени уравнения (1) задается прямым методом Эйлера:
$$display$$frac{( φ^{t+∆t}-φ^t)}{∆t}+F^tcdot∇φ^t=0 qquad (4) $$display$$
где:
$inline$φ^t$inline$ — текущие значения $inline$φ $inline$ в момент времени $inline$t $inline$
$inline$F^t$inline$ — вектор скорости в момент времени $inline$t $inline$
$inline$∇φ^t$inline$ — значения градиента $inline$φ$inline$ в момент времени $inline$t $inline$
При вычислении градиента необходимо проявлять большую осторожность в отношении пространственных производных $inline$φ$inline$. Это лучше всего видно, если рассмотреть расширенный вид уравнения (4):
$$display$$frac{(φ^{t+∆t}-φ^t)}{∆t}+u^t φ_x^t+v^t φ_y^t+w^t φ_z^t=0 qquad (5)$$display$$
где $inline$u, v, w$inline$ — компоненты $inline$x, y, z$inline$ из $inline$F$inline$. Для простоты рассмотрим одномерную форму уравнения (5) в конкретной точке сетки $inline$x_i$inline$:
$$display$$frac{(φ^{t+∆t}-φ^t)}{∆t}+u_i^t cdot(φ_x )_i^t=0 qquad (6)$$display$$
где $inline$(φ_x )_i^t $inline$ — производная $inline$φ$inline$ по пространству в точке $inline$x_i$inline$. Для того, чтобы понять, какую разностную схему использовать, прямую или обратную, будем основываться на знаке $inline$u_i$inline$ в точке $inline$x_i$inline$. Если $inline$u_i>0$inline$, значения $inline$φ$inline$ перемещаются слева направо, и поэтому следует использовать обратные разностные схемы ( $inline$D_x^-$inline$ в уравнениях 7). Напротив, если $inline$u_i<0$inline$, то для приближения $inline$φ_x$inline$ следует использовать прямые разностные схемы ($inline$D_x^+$inline$ в уравнениях 7). Именно этот процесс выбора аппроксимации для производной $inline$φ$inline$ по пространству, основанный на знаке $inline$u_i$inline$, известен как расчет по потоку.
В двумерном случае для вычисления $inline$φ$inline$ нам требуются производные, расписанные ниже. Стоит упомянуть, что мы делаем предположение изотропности изображения.
$$display$$begin{matrix} D_x=frac{φ_{i+1,j}-φ_{i-1,j} }2qquad D_x^+=frac{φ_{i+1,j}-φ_{i,j}}2qquad D_x^-=frac{φ_{i,j}-φ_{i-1,j}}2\ D_y=frac{φ_{i,j+1}-φ_{i,j-1} }2qquad D_y^+=frac{φ_{i,j+1}-φ_{i,j}}2qquad D_y^-=frac{φ_{i,j}-φ_{i,j-1}}2 end{matrix} qquad (7)$$display$$
$inline$∇φ$inline$ аппроксимируется с использованием схемы upwind:
$$display$$∇φ_{max}= begin{bmatrix} sqrt{max(D_x^+,0)^2+max(-D_x^-,0)^2} \ sqrt{max(D_y^+,0)^2+max(-D_y^-,0)^2} end{bmatrix} qquad (8)$$display$$
$$display$$∇φ_{min}= begin{bmatrix} sqrt{min(D_x^+,0)^2+min(-D_x^-,0)^2} \ sqrt{min(D_y^+,0)^2+min(-D_y^-,0)^2} end{bmatrix} qquad (9)$$display$$
Наконец, в зависимости от того, является ли $inline$F_{i,j,k}>0$inline$ или $inline$F_{i,j,k}<0$inline$, $inline$∇φ$inline$ представляется, как:
$$display$$∇φ = begin{cases} ‖∇φ_{max} ‖_2 & quad text{если } F_{i,j,k}>0 \ ‖∇φ_{min} ‖_2 & quad text{если } F_{i,j,k}<0 \ end{cases} qquad (10)$$display$$
$$display$$φ(t+∆t)=φ(t)+ ∆tF|∇φ|qquad (11)$$display$$
Коэффициент F скорости, как обсуждалось ранее, основан на значениях интенсивности пикселов и значениях кривизны.
Кривизна
Будем вычислять ее на основе значений текущего уровня, установленных с использованием приведенных ниже производных. В двух измерениях требуется только $inline$D_x^{+y},D_x^{-y},D_y^{+x},D_y^{-x}$inline$, наряду с определенными ранее производными:
$$display$$begin{matrix} D_x^{+y}=frac{(φ_{i+1,j+1}-φ_{i-1,j+1})}2 qquad D_x^{-y}=frac{(φ_{i+1,j-1}-φ_{i-1,j-1})}2 \ D_y^{+x}=frac{(φ_{i+1,j+1}-φ_{i+1,j-1})}2 qquad D_y^{-x}=frac{(φ_{i-1,j+1}-φ_{i-1,j-1})}2 end{matrix} qquad (12)$$display$$
Используя разность нормалей, кривизна вычисляется с использованием указанных выше производных с двумя нормалями $inline$n^+$inline$ и $inline$n^-$inline$.
$$display$$n^+= begin{bmatrix} frac{D_x^+}{sqrt{(D_x^+)^2+(frac{D_y^{+x}+D_y}{$$display$$
2})^2}} \
frac{D_y^+}{sqrt{(D_y^+)^2+(frac{D_x^{+y}+D_x}{2})^2}} \
end{bmatrix} qquad (13)
$$display$$$$display$$
n^-=
begin{bmatrix}
frac{D_x^-}{sqrt{(D_x^-)^2+(frac{D_y^{-x}+D_y}{2})^2}} \
frac{D_y^-}{sqrt{(D_y^-)^2+(frac{D_x^{-y}+D_x}{2})^2}} \
end{bmatrix} qquad (14)
$$display$$ Две нормали используются для вычисления дивергенции, с помощью которой мы вычисляем среднюю кривизну, как показано ниже:$$display$$
H=frac{1}{2}∇cdotfrac{∇φ}{|∇φ|} =frac{1}{2}((n_x^+-n_x^- )+(n_y^+-n_y^- ))qquad (15)
$$display$$
Устойчивость
Устойчивость вытекает из условия Куранта-Фридрихса-Леви (CFL), которое утверждает, что скорость движения информации в вычислительной схеме должна быть такой, что за время $inline$∆t$inline$ вы не выходите за рамки одной ячейки, то есть $inline$frac{∆x}{∆t}>|u|$inline$. Имеем: $$display$$
∆t<frac{∆x}{max{|u|}} qquad (16)$$display$$
Последовательная реализация
Реализуем данный алгоритм бинарной сегментации в системе Matlab. Сделаем это, в первую очередь, для наглядности, так как Matlab прекрасно справляется с работой с таблицами. Также там есть очень простые функции, позволяющие считывать изображения и выводить работу алгоритма на экран. Благодаря этому код будет сжатым и понятным. Естественно, реализация, например на C будет куда выгоднее с точки зрения скорости. Но в данной статье мы не гонимся за скоростью, а пытаемся разобраться в методе.
Псевдокод алгоритма можете видеть ниже:
- Вход: Оригинальное изображение I; исходная маска m; порог T; ошибка ε; количество итераций N; число, показывающее через какое количество итераций пересчитываем карту расстояний, ITS.
- Выход: Результат сегментации – изображение seg.
Инициализируем φ_0 с помощью Signed Euclidean Distance Transform (SEDT) и маски m.
Высчитываем D(I)= ε-|I-T|. - Цикл i от 1 до N
- Высчитываем производные первого порядка
- Высчитываем производные второго порядка
- Высчитываем значения нормалей $inline$n^+$inline$ и $inline$n^-$inline$
- Вычисляем значение градиента $inline$∇φ$inline$
- Вычисляем значение функции $inline$F= αD(I)+(1-α)∇cdotfrac{∇φ}{|∇φ|}$inline$
T$inline$, диапазона $inline$ε$inline$ и взвешивания кривизны $inline$alpha$inline$, запускает пусковую установку и затем переходит к рисованию замкнутого многоугольника, который будет формировать начальную маску (обеспечивающую некоторую базовую интерактивность). Итак, считываем изображение и сразу же создаем нулевую матрицу $inline$m$inline$, которая будет нашей маской:
I = imread('test_output.pgm'); I = imresize(I, 1); init_mask = zeros(size(I,1),size(I,2)); Для создания маски удобно выбирать координаты центра и отклонения от него. Получим прямоугольник, заполненный единицами. Его и будем передавать в ядро.
x = 400; y = 800; %координаты центра маски dx = 10; dy = 10; init_mask(y - dy : y + dy, x - dx : x + dx) = 1; %заполняем единицами seg = simpleseg(I, init_mask, max_its, E, T); %Запускаем ядро программы Теперь рассмотрим функцию simpleseg, которая и является ядром кода. Вначале нужно получить SDF из маски init_mask:
phi = mask2phi(init_mask); %получаем SDF function phi = mask2phi(init_a) %функция получения SDF phi=bwdist(init_a)-bwdist(1-init_a); Напишем функцию, которая будет высчитывать кривизну:
%Вычисление кривизны function curvature = get_curvature(phi) dx = (shiftR(phi)-shiftL(phi))/2; dy = (shiftU(phi)-shiftD(phi))/2; dxplus = shiftR(phi)-phi; dyplus = shiftU(phi)-phi; dxminus = phi-shiftL(phi); dyminus = phi-shiftD(phi); dxplusy = (shiftU(shiftR(phi))-shiftU(shiftL(phi)))/2; dxminusy = (shiftD(shiftR(phi))-shiftD(shiftL(phi)))/2; dyplusx = (shiftR(shiftU(phi))-shiftR(shiftD(phi)))/2; dyminusx = (shiftL(shiftU(phi))-shiftL(shiftD(phi)))/2; nplusx = dxplus./sqrt(eps+(dxplus.^2 )+((dyplusx+dy )/2).^2); nplusy = dyplus./sqrt(eps+(dyplus.^2 )+((dxplusy+dx )/2).^2); nminusx= dxminus./sqrt(eps+(dxminus.^2)+((dyminusx+dy)/2).^2); nminusy= dyminus./sqrt(eps+(dyminus.^2)+((dxminusy+dx)/2).^2); curvature = ((nplusx-nminusx)+(nplusy-nminusy))/2; Производные вычисляются вычитанием сдвинутых матриц функции $inline$φ$inline$. Обратите внимание, что производные не вычисляются поэлементно, так как это было бы менее эффективно.
%-- Вычисление производных с помощью сдвига матриц function shift = shiftD(M) shift = shiftR(M')'; function shift = shiftL(M) shift = [ M(:,2:size(M,2)) M(:,size(M,2))]; function shift = shiftR(M) shift = [M(:,1) M(:,1:size(M,2)-1)]; function shift = shiftU(M) shift = shiftL(M')'; Теперь считаем коэффициент скорости $inline$F$inline$
alpha=0.5; D = E - abs(I - T); K = get_curvature(phi); F = alpha*single(D) + (1-alpha)*K; После переходим к обновлению уровней. Для этого сначала высчитываем градиент для соблюдения устойчивости:
dxplus = shiftR(phi)-phi; dyplus = shiftU(phi)-phi; dxminus = phi-shiftL(phi); dyminus = phi-shiftD(phi); gradphimax_x = sqrt(max(dxplus,0).^2+max(-dxminus,0).^2); gradphimin_x = sqrt(min(dxplus,0).^2+min(-dxminus,0).^2); gradphimax_y = sqrt(max(dyplus,0).^2+max(-dyminus,0).^2); gradphimin_y = sqrt(min(dyplus,0).^2+min(-dyminus,0).^2); gradphimax = sqrt((gradphimax_x.^2)+(gradphimax_y.^2)); gradphimin = sqrt((gradphimin_x.^2)+(gradphimin_y.^2)); gradphi = (F>0).*(gradphimax) + (F<0).*(gradphimin); dt = .5/max(max(max(abs(F.*gradphi)))); И изменяем функцию набора уровней $inline$φ$inline$:
phi = phi + dt.*(F).*gradphi;
Будем выводить промежуточный результат на экран каждые 20 итераций:
if(mod(its,20) == 0)
showcontour(I,phi,its);
subplot(2,2,4); surf(phi); shading flat;
end
С помощью функции showcontour:
function showcontour(I, phi, i)
subplot(2, 2, 3); title('Evolution') ;
imshow (I);
hold on;
contour(phi, [0 0],'g','LineWidth', 2);
hold off ; title([num2str(i) 'Iterations'] ); drawnow;
Результаты
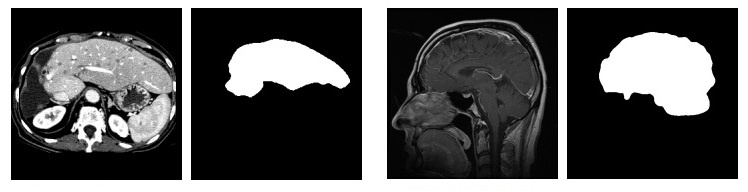
Я проводил тесты алгоритма на двух типах изображений: медицинских и изображений горных пород (так как решал эту задачу на дипломе).
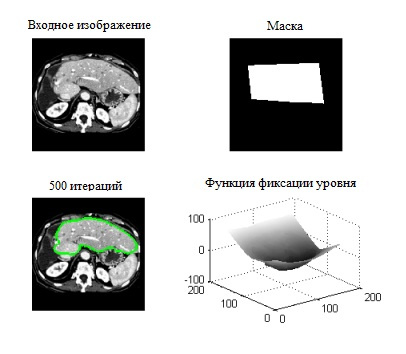
Для медицинских изображений это работает вот так:
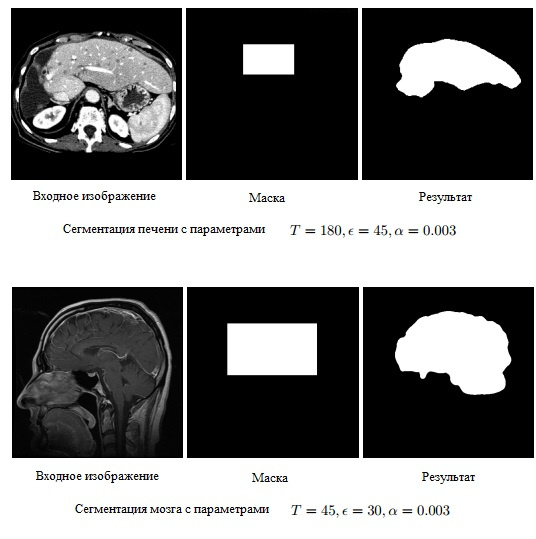
Мы видим, что алгоритм очень хорошо справляется с данной задачей.
Стоит сказать о том, что данный алгоритм можно реализовать для трехмерного случая. В этой статье я не буду расписывать особенности, но покажу как это работает:

В этом случае начальная маска — это куб (в общем случае, конечно, это любое трехмерное тело)
В сегментации изображений горных пород в первую очередь сталкиваешься с проблемой шума. Это связано со многими причинами: начиная от погрешности томографов, заканчивая ошибками в обратном преобразовании Радона (именно так получаются такие изображения). Именно поэтому сначала нужно изображения отфильтровать. Очень хорошо с этим справляется фильтр анизотропной диффузии Перона и Малика. Ссылка на статью об этом фильтре уже была в начале статьи. Оставлю ее и в конце поста.
Вот, что происходит, если сегментировать зашумленное изображение:
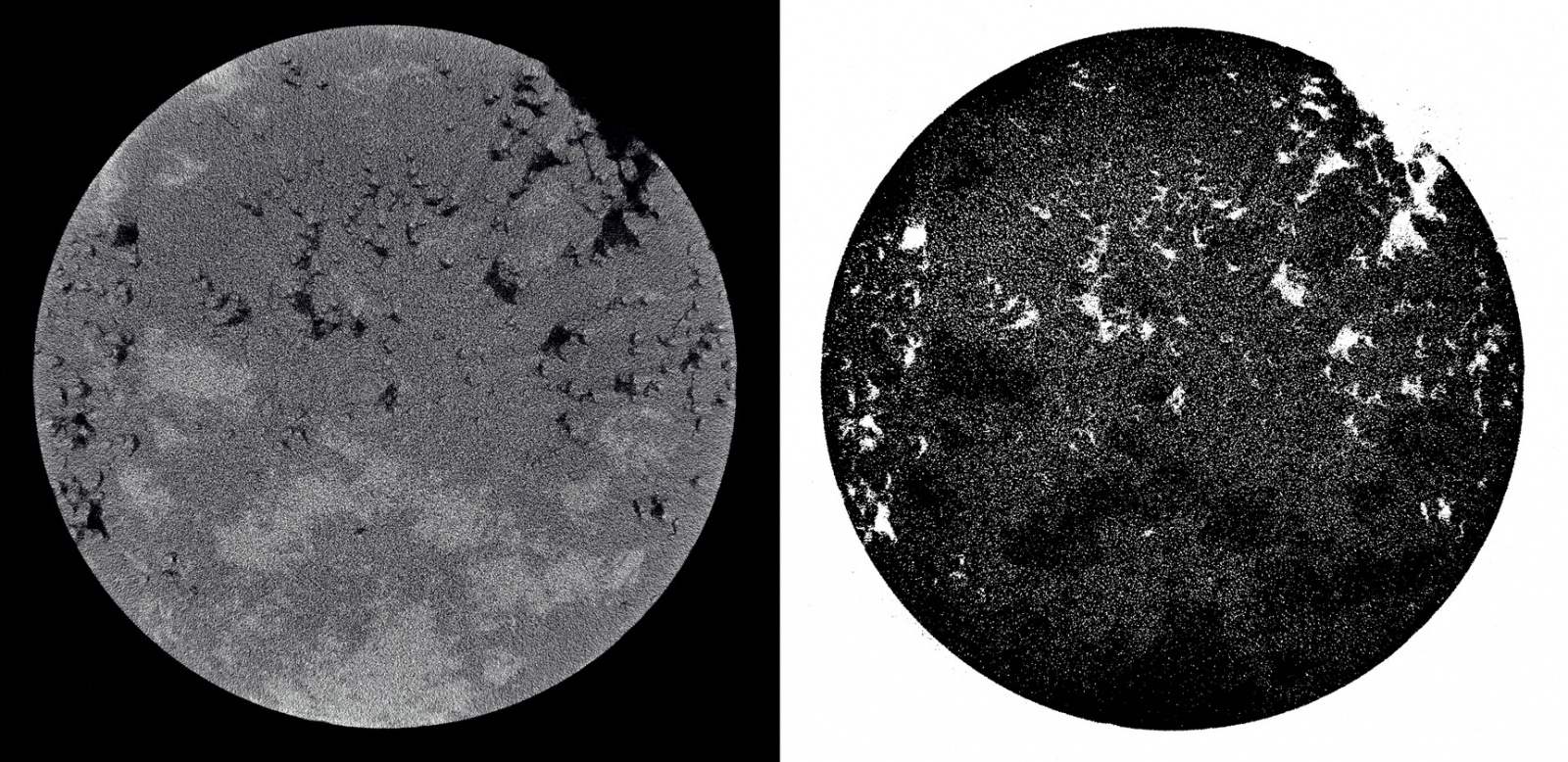
А вот, что с отфильтрованным изображением:
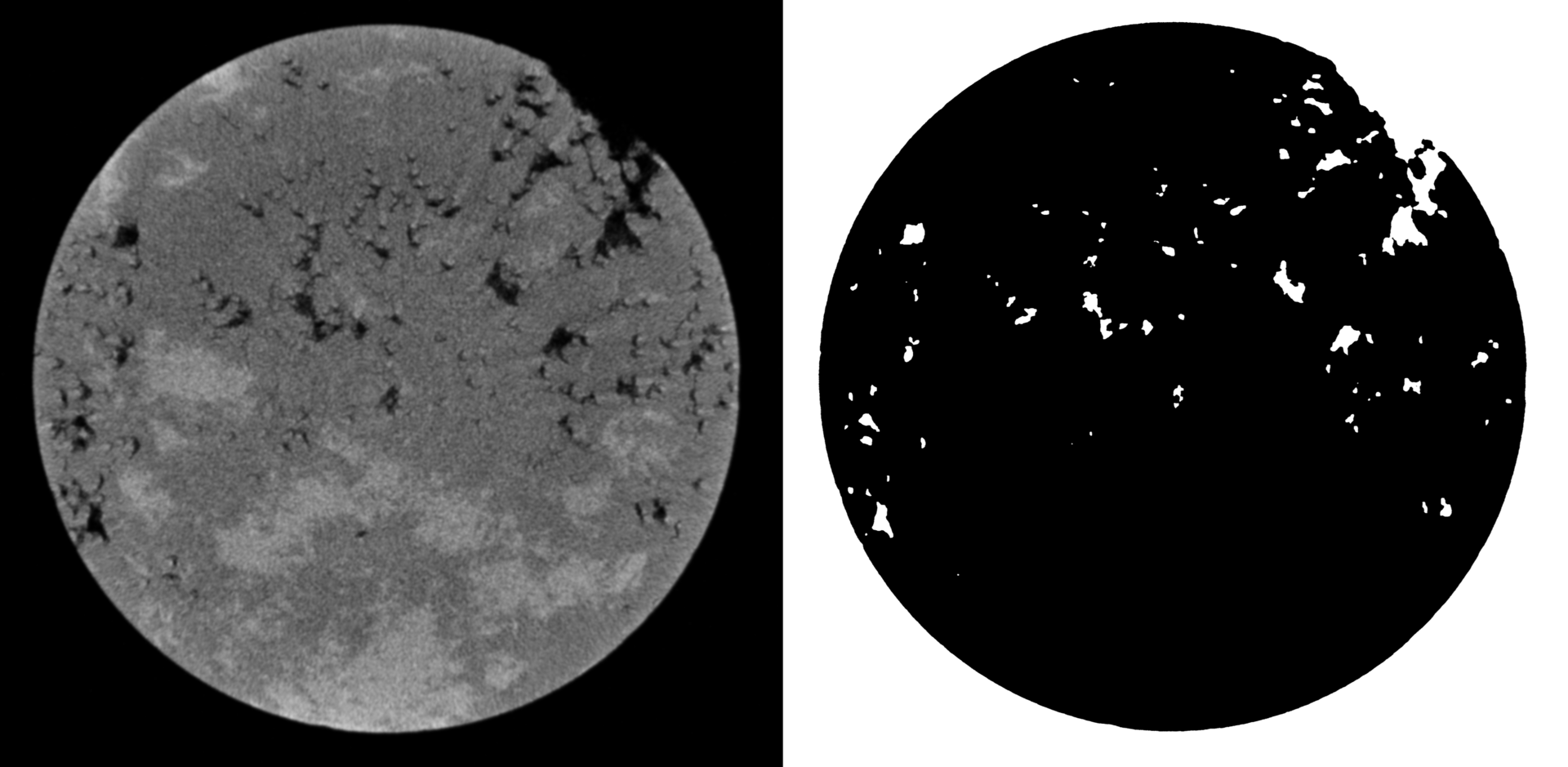
Выводы и дальнейшая работа
Метод фиксации уровня это отличный метод для проведения бинарной сегментации. Основным его недостатком является большая вычислительная сложность. Время, за которое Matlab на моей машине обрабатывал изображение 512х512 (было проведено 5000 итераций) составляет 2737.84 секунд (45 минут). Это, конечно, неимоверно много.
Но не стоит закрывать статью после прочтения этого факта. Самой главной причиной выбора мной этого алгоритма было то, что он очень хорошо параллелится. Я это делал с помощью CUDA, вы можете использовать что-то другое и написать об этом, например, в комментариях. Если кому-то интересно, то в перспективе буду писать следующую статью на тему распараллеливания этого алгоритма.
P.S. Вот ссылки на исходные коды: стартовый файл и функция, непосредственно отвечающая за сегментацию.
Источники
Автор: 22dla