В этой статье предлагаются правила для двумерного клеточного автомата, который, с одной стороны очень похож на игру Жизнь Джона Конвея (Conway’s Game of Life), а с другой — обладает существенными отличиями. Прежде всего, его отличает увеличенное до трех количество состояний клеток, повышенная способность к самоорганизации, неограниченное время активной эволюции и неограниченное количество движущихся конфигураций.
Для стабильных конфигураций новые правила совпадают с правилами игры Жизнь, поэтому все стабильные конфигурации в игре Жизнь существуют и в новых правилах. В описываемом клеточном автомате существует большой класс движущихся конфигураций, космических кораблей. Все эти конфигурации перемещаются по одному и тому же поступательному механизму, который напоминает движение и шагового экскаватора и человека на костылях. Подобные космические корабли я назвал степпер (stepper), а само правило Steppers. Так его и будем называть в дальнейшем.
В Steppers существует довольно много осцилляторов, причем, некоторые осцилляторы из игры Жизнь работают и в Steppers, что говорит о преемственности правил. И, наконец, знаменитый глайдер Конвея, так же существует в предлагаемых правилах. В статье будет рассмотрена динамика случайным образом заполненных решеток, раскрыт механизм движения степперов, описаны найденные на данный момент осцилляторы и степперы. Так же будут приведены примеры столкновений и сложного функционального поведения.
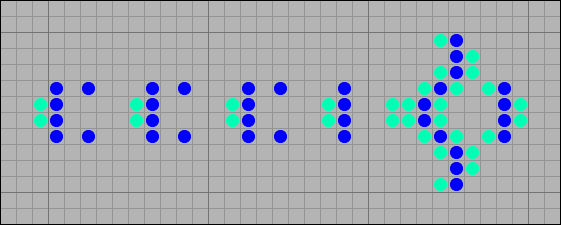
[00] Пример движущейся конфигурации, генерирующей поток степперов
История разработки правил
В 1988 году я работал в лаборатории технического зрения. Изучая алгоритм скелетонизации растрового монохромного изображения, я написал программу для его реализации. Сам алгоритм скелетонизации нам так и не пригодился и был заброшен, а написанная программа после небольшой доработки оказалась вполне приличным клеточным автоматом с графическим редактором и графическим выводом. Первым испытанием для неё, конечно же, оказалась игра Жизнь Джона Конвея. Через некоторое время, мне захотелось поэкспериментировать с другими правилами, и я вспомнил про прочитанную ранее статью "Эволюция игры Эволюция" в журнале «Наука и жизнь» за 1975 год [1]. В этой статье, пытаясь развить игру Жизнь, автор И. Сидоров добавил третье состояние для вновь рожденных клеток. По новым правилам клетка может находиться в трех состояниях, пустая, молодая и старая. Молодая клетка не погибает ни при каких обстоятельствах, и в следующем поколении становится старой.

[01] Обозначение состояний клеток
Полностью все правила И. Сидоров сформулировал в следующем виде:
- Молодая клетка в течение одного хода не умирает ни от перенаселенности, ни от одиночества. Через один ход молодая клетка превращается в старую.
- В каждой пустой клетке рождается новая (молодая) клетка, если эта клетка имела трех соседей (соседями могли быть как старые, так и молодые клетки).
- Старая клетка умирает от перенаселенности, если она граничит с четырьмя (и более) старыми клетками или если она граничит с тремя (и более) клетками, среди которых есть хоть одна молодая.
- Старая клетка умирает от одиночества, если она изолирована или имеет только одного соседа (соседом может быть как старая, так и молодая клетка).
В клеточном автомате И. Сидорова имеются два, описанных им, корабля. Позднее мне удалось найти два осциллятора. К сожалению, при превышении некоторой критической массы, популяция теряет структуру и быстро растет. Так как наблюдать за этим было неинтересно, я взялся разрабатывать свои законы жизни и смерти.
После отбора различных вариантов были сформированы следующие правила:
- Молодая клетка в течение одного хода не умирает ни от перенаселенности, ни от одиночества. Через один ход молодая клетка превращается в старую (это правило оставлено без изменений).
- На пустой клетке рождается молодая клетка, если у неё ровно три соседа, среди которых есть хотя бы две старые клетки.
- Старая клетка продолжает существовать в следующем поколении, если у неё две или три соседние клетки, среди которых не более одной молодой.
Более наглядно правила можно представить в виде таблиц. По осям отложено количество молодых и старых соседей.
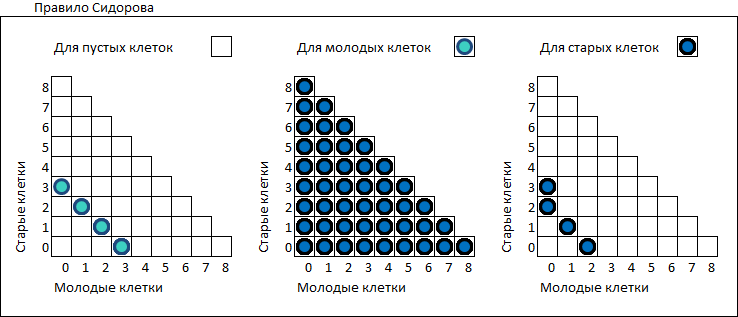
[02] Табличное представление правила И. Сидорова
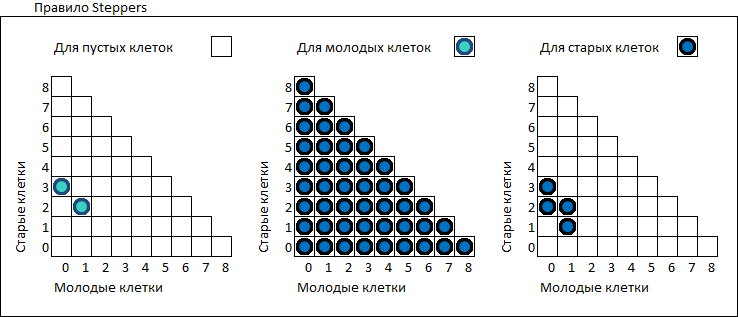
[03] Табличное представление правила Steppers
Это правило показалось мне настолько интересным, что я написал свою статью, и отправил ее в тот же журнал «Наука и Жизнь». Через некоторое время я получил ответ, что в ближайшее время публикаций по клеточным автоматам не планируется. Больше двадцати лет я потихоньку, с большими перерывами занимался этим клеточным автоматом, но не предпринимал попыток где-либо его опубликовать. И только с появлением замечательной программы Golly, в которой можно создавать клеточные автоматы по произвольным правилам, появилась и возможность поделиться своими скромными исследованиями. Программа Golly бесплатна, её можно загрузить с сайта http://sourceforge.net/projects/golly/.
Все иллюстрации в этой статье проиндексированы, при желании можно загрузить архив MilhinSA.Golly2.5.zip в котором под соответствующим индексом находятся rle-файлы со всеми примерами. В этом случае, можно не довольствоваться статическими картинками, а увидеть процесс в действии. Программа Golly может открыть этот архив с правилом и примерами без предварительной распаковки.
В марте 2012 года я опубликовал сообщение о клеточном автомате Steppers на англоязычном форуме Conway's Game of Life. Сообщение вызвало определенный интерес среди участников форума, некоторые из них приняли участие в исследовании Steppers и поделились своими находками.
Динамика
Лучший способ проверить интегральные характеристики клеточного автомата, это подать на его вход шумовой сигнал, или, другими словами, случайным образом заполненную популяцию. На следующем рисунке показаны результаты эволюции случайным образом заполненной тороидальной сетки игры Жизнь и Steppers в поколениях 32, 320 и 3200. Видно, что плотность популяции Steppers падает медленнее, чем в игре Жизнь и на каком-то этапе стабилизируется.
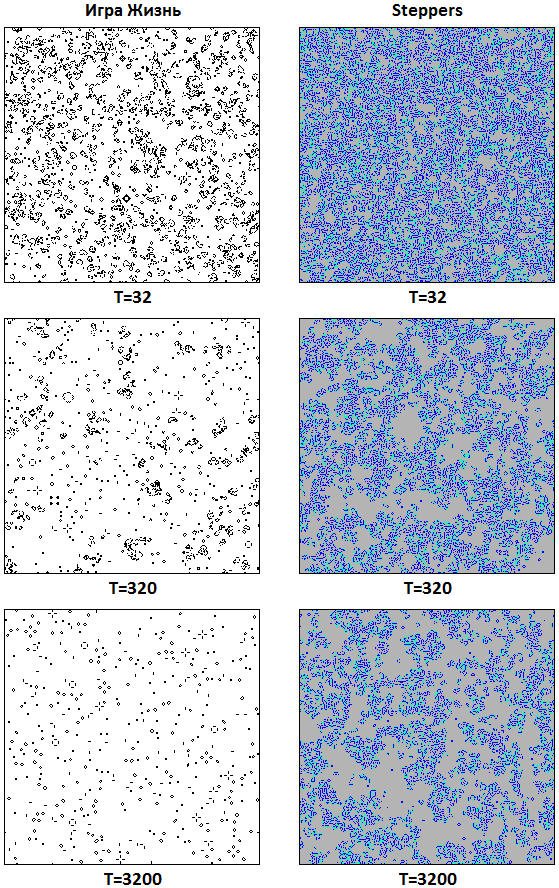
[04] Эволюция случайной популяции игры Жизнь и Steppers
Для получения статистически достоверных данных был проведен следующий вычислительный эксперимент. Для каждого правила было сформировано случайно заполненное тороидальное поле размером 256 х 256 клеток с плотностью 50%. Клеточный автомат отрабатывал до 10 000 поколений. Для каждого поколения вычислялась плотность поля в процентах, а также процент клеток изменивших своё состояние. Последний параметр характеризует активность клеточного автомата. Для каждого автомата этот процесс повторялся 1000 раз, затем выходные данные усреднялись.
Ниже показаны графики плотности и активности. Из этих графиков видно, что плотность и, соответственно, активность игры Жизнь быстро падает в самом начале развития и в 3000-4000 поколении уменьшается в среднем до 3 % плотности. Активность падает, в среднем до 1%. Легко понять, что это оставшиеся стационарные конфигурации и простые осцилляторы. Клеточный автомат Steppers эволюционирует по другому сценарию. На протяжении примерно 20 поколений устанавливается баланс между молодыми и старыми ячейками, что приводит к затухающему колебательному процессу. Затем плотность начинает уменьшаться, и в 500-700 поколении стабилизируется на 21%. Активность стабилизируется на 14%. Таким образом, эволюция случайного поля достаточного размера продолжается неопределенно долго.
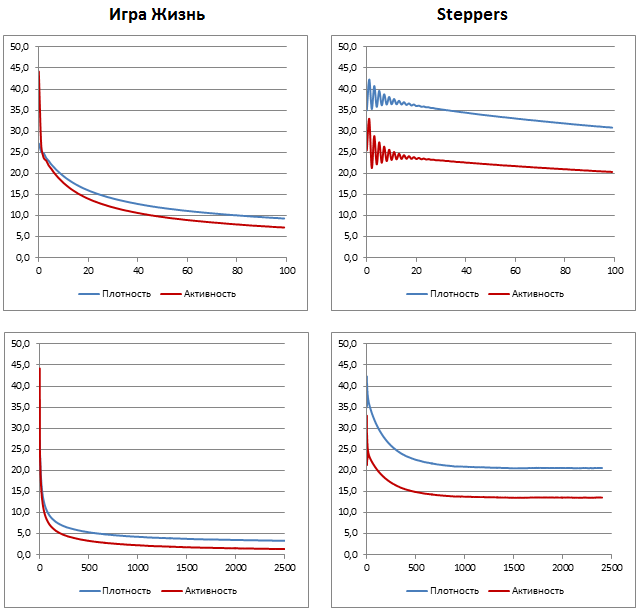
[05] Графики изменения плотности и активности
Графики изменения плотности и активности показывают среднее значение для всего поля, но плотность и активность клеток меняется не только во времени, но и в пространстве. При эволюции равномерно-заполненного случайного поля видно, что клетки группируются в активные области, формируя некоторую текстуру. Чтобы выделить области с повышенной активностью был применен специальный алгоритм отображения клеточного автомата. Работает он следующим образом. Для каждой ячейки на протяжении 32 поколений подсчитывается количество рождений и смертей. Затем выводится изображение клеточного автомата в палитре черный-красный-желтый-белый. Следующий рисунок показывает, что активные ячейки в игре Жизнь довольно быстро распадаются на изолированные области, которые впоследствии затухают. В клеточном автомате Steppers активные области непрерывно меняют форму и размеры, сливаются и распадаются. Достаточно большие площади остаются свободными и в них существуют стационары, осцилляторы, а так же глайдеры и степперы. Благодаря этому, даже при эволюции случайного поля в результате самоорганизации возникает довольно интересная картина, за которой интересно наблюдать.
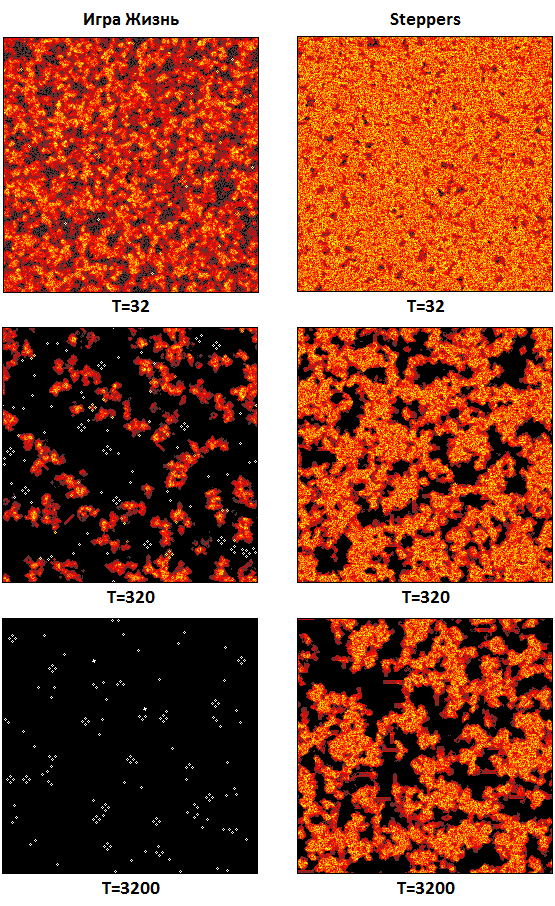
[06] Изменение активности популяции в процессе эволюции
Следует признать, что правило Stepper, не только очень живучее, но и очень взрывоопасное. Часто, взаимодействие простейших конфигураций ведет к неудержимому росту популяции. На форуме Conway's Game of Life были найдены конфигурации минимального размера, вызывающие неограниченный рост популяции. На следующем рисунке изображен 5-клеточный паттерн, а также его состояние в 1500 поколении, причем, не полностью. Размер популяции немногим меньше 20 000 клеток.
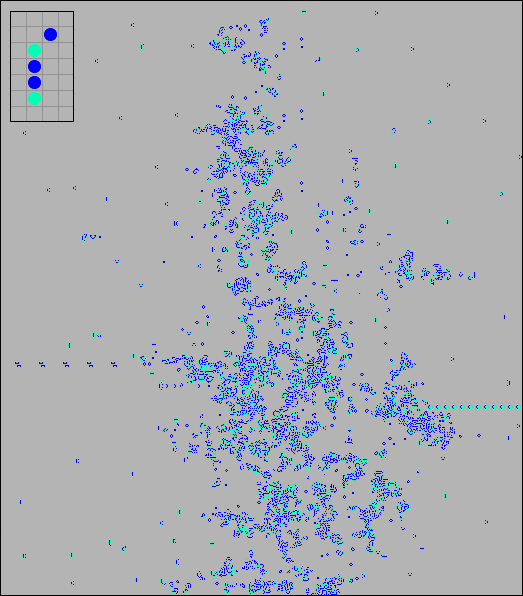
[07] 5-клеточный паттерн в 1500-м поколении
Еще интенсивнее развивается линейный 7-клеточный паттерн. Здесь он изображен в 500 поколении, размер популяции 8 124 клетки. В 3000 поколении размер популяции превысит 500 000 клеток.
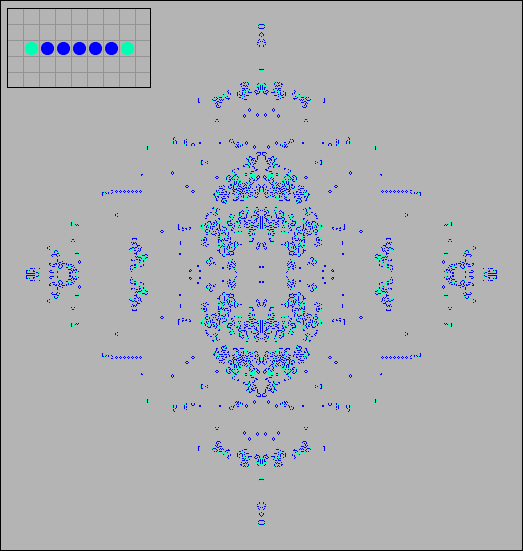
[08] 7-клеточный паттерн в 500-м поколении
Движение, степперы
В клеточном автомате Steppers, на данный момент, обнаружены два типа движущихся конфигураций. Причем, к первому типу относится единственная конфигурация, называемая в игре Жизнь глайдером. Видно, что глайдер в Steppers очень незначительно отличается от глайдера из игры Жизнь. При столь существенном различии этих правил, существование глайдеров было довольно неожиданным.
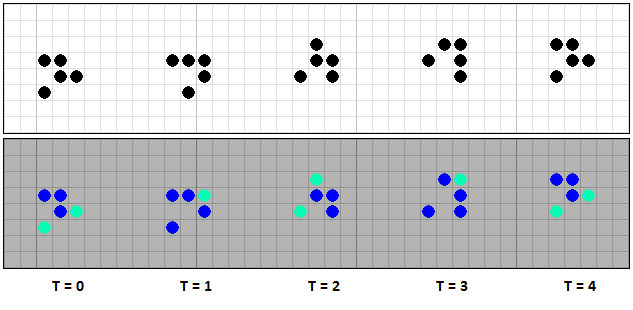
[09] Сравнение глайдеров игры Жизнь и Steppers
К другому типу относятся степперы, и их количество неограничено, так как неограничен их размер. Все степперы объединяются одним и тем же способом передвижения. И этот способ обязан своему существованию правилу о рождении. Напомню, звучит оно так «На пустой клетке рождается молодая клетка, если у неё ровно три соседа, среди которых есть хотя бы две старые клетки». Попробую объяснить, почему правило о рождении вызвало такой эффект.
В игре Жизнь существует такое понятие, как скорость света. Это предельная скорость, с которой может двигаться бесконечный или замкнутый ряд клеток и она равна одной ячейке за поколение. В Steppers ряд из молодых клеток не может породить новый ряд, для этого ему сначала нужно состариться. Поэтому скорость распространения бесконечного ряд клеток в Steppers вдвое ниже, чем в игре Жизнь и составляет одну клетку за два поколения.
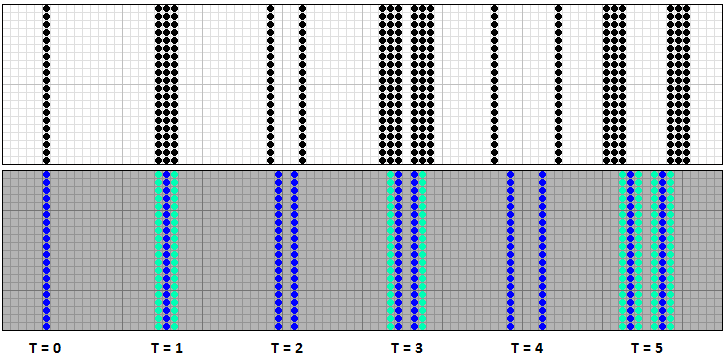
[10] Эволюция бесконечного ряда клеток в игре Жизнь и Steppers
Теперь рассмотрим эволюцию конечного ряда клеток. В игре Жизнь напротив крайних клеток не может родиться новая ячейка, так как у неё только два соседа, поэтому каждое последующее поколение новый ряд становится на две ячейки короче, и через некоторое время сходит на нет. Та же картина наблюдается при эволюции ряда клеток в КА Steppers, только в два раза медленнее.
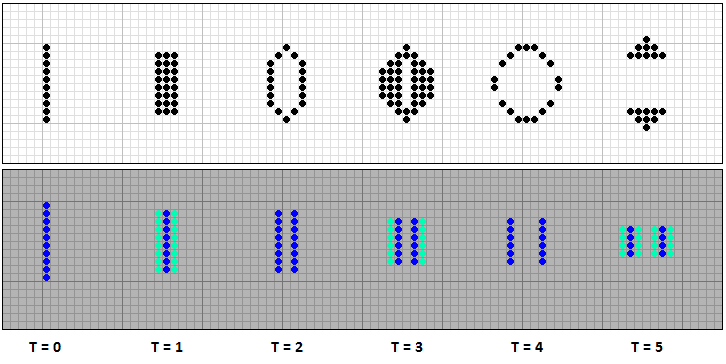
[11] Эволюция конечного ряда клеток в игре Жизнь и Steppers
Но если в Steppers с одной стороны ряда добавить к крайним клеткам по одному соседу, чтобы она не вымерла в первом поколении, картина совершенно меняется. Добавить соседей можно одним из следующих способов.
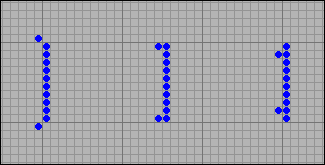
[12] Превращение ряда клеток в степпер
В этом случае на этапе старения по краям ряда рождается по одной клетке, и его ширина восстанавливается. Две старые и одна молодая ячейки уже могут породить новую ячейку и, таким образом, ряд клеток продолжает двигаться, непрерывно восстанавливая свою ширину.
[13] Восстановление ширины ряда клеток
Используя этот прием можно создать степпер любого размера. Ниже показан ряд из 100 клеток и изящный степпер, который получился из него через несколько сотен поколений. Его период равен восьми.
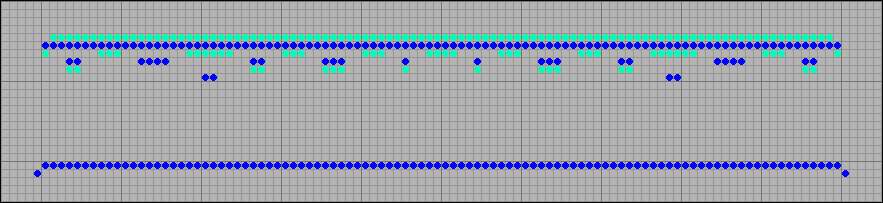
[14] 100-клеточный степпер
Степперы могут быть смежными или составными, они могут тесно взаимодействовать или вовсе двигаться как одно целое. Вот небольшой пример различных степперов.
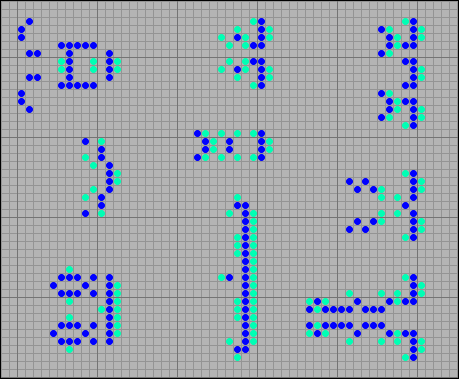
[15] Примеры степперов
Размеры степперов могут быть неограниченно большими не только в ширину, но и в длину. Как показал участник форума Conway's Game of Life Эмерсон Дж. Перкинс (Emerson J. Perkins (knightlife)), используя регулярные элементы в произвольном порядке можно сконструировать степпер произвольной длины.
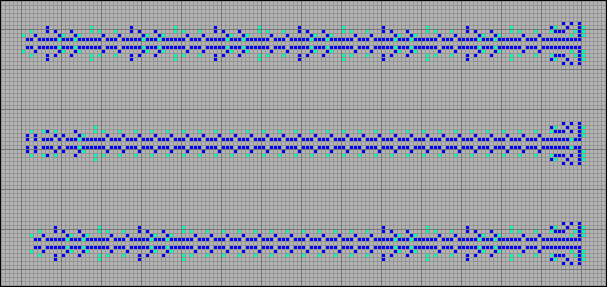
[16] Конструирование степпера произвольной длины
К сожалению, на данное время неизвестны другие типы движущихся конфигураций кроме глайдеров и степперов. Но я все-таки надеюсь, что они существуют. Изображенные выше степперы не оставляют после себя никаких конфигураций, то есть являются космическими кораблями. Другие степперы в процессе движения могут оставлять различные стационарные конфигурации, испускать глайдеры и степперы, а часто за ними следует просто неутихающий хаос.
Паровозы и грабли
В соответствии с терминологией игры Жизнь, движущиеся конфигурации, оставляющие за собой мусор называются паровозами (puffers). На следующем рисунке можно увидеть подборку паровозов, которые при движении оставляют за собой цепочку из стационарных конфигураций. Паровоз, порождающий цепочку из двух блоков, отличается рекордно маленьким периодом, p6. При скорости движения c/2, блоки укладываются с периодом всего в три клетки. Ближе просто невозможно. Последний паровоз и вовсе формирует непрерывную линию. Это позволяет отнести его к классу удлинителей фитилей (wickstretcher).
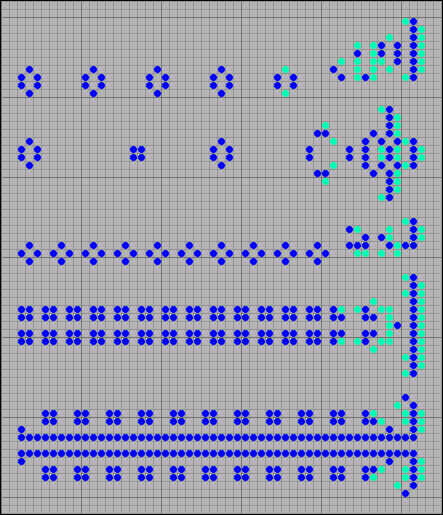
[17] Паровозы
Паровозы, порождающие движущиеся конфигурации, называются граблями (rake). Столь неожиданное название, является следствием неточного перевода. Согласно словарю Мюллера, слово rake имеет множество значений, в том числе и военно-морское «обстреливать продольным огнем». Подозреваю, что именно это имелось в виду авторами термина rake. Но у нас прижились грабли, придется с этим смириться. В зависимости от направления стрельбы грабли делятся на передние, боковые и обратные. В Steppers грабли стреляют глайдерами и степперами. Ниже можно увидеть различные варианты граблей-стрелялок.
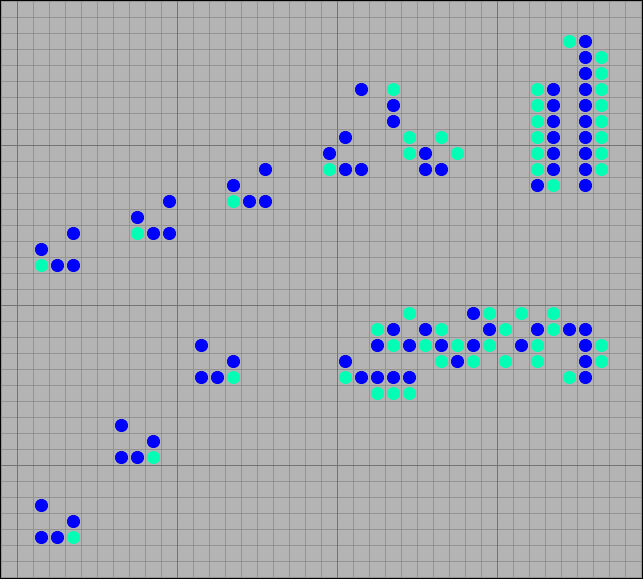
[18] Грабли, стреляющие глайдерами, передние и обратные
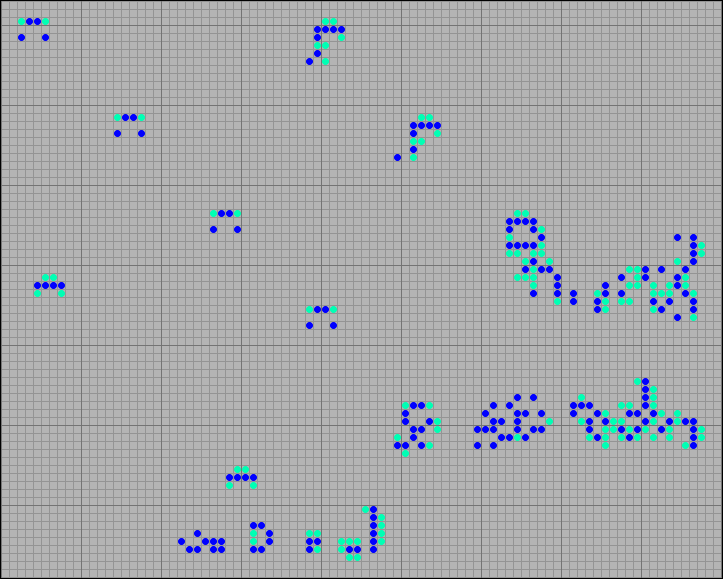
[19] Боковые грабли

[20] Обратные грабли
Не все паровозы обладают столь узкой специализацией. Паровозы на следующем рисунке наряду со стационарными конфигурациями выпускают обратные степперы.
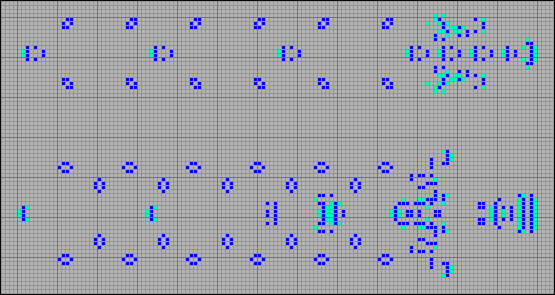
[21] Обратные грабли плюс стационарные конфигурации
А этот паровоз оставляет после себя за один период две баржи, два ботика, четыре боковых степпера и четыре обратных, в том числе один большой степпер шириной 12 клеток.
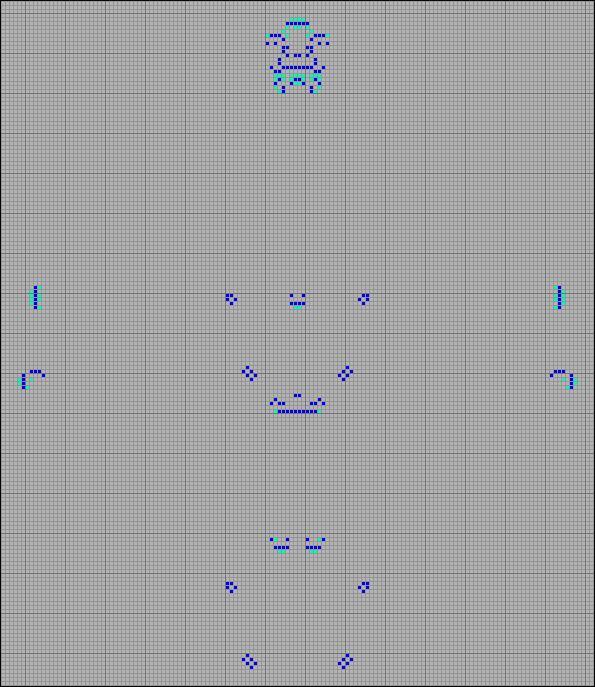
[22] Обратные, боковые грабли плюс стационарные конфигурации
К сожалению, до сих пор не найдены паровозы оставляющие после себя осцилляторы, периодические конфигурации. На самом деле существует паровоз порождающий пару бакенов, но их трудно заметить на фоне прочего мусора. Так что это, скорее, исключение из правила.
Размножители
Размножители (breeders) это конфигурации обеспечивающие квадратичный рост популяции. Суть квадратичного роста в том, что размножитель порождает конфигурации, которые, в свою очередь, тоже порождают некоторые конфигурации. В Steppers имеются два типа размножителей, это грабли стреляющие граблями и грабли стреляющие паровозами, оставляющими стационарные конфигурации (надеюсь, что это предложение никогда не вырвут из контекста).
На следующем рисунке можно увидеть размножитель, типа MMS (moving-moving-stationary). Это обозначает, что движущийся объект порождает движущийся, который порождает стационарные объекты. С периодом p240 он выпускает четыре паровоза, которые формируют цепочку из бадей.
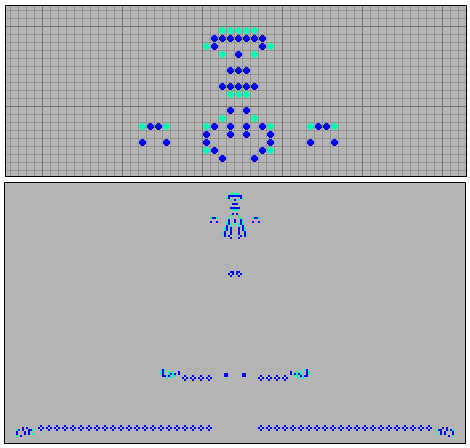
[23] Размножитель типа MMS
Следующий размножитель относится к типу MMM (moving-moving-moving). С периодом p32 он выпускает грабли стреляющие простыми степперами. Следует отметить небольшой размер этого размножителя, всего 15 клеток ограниченных прямоугольником в 5×9 клеток. В игре Жизнь наименьшая конфигурация, обладающая квадратичным, ростом это «26-cell quadratic growth», его размер, как видно из названия, 26 клеток, а размер и вовсе 16193×15089 клеток.
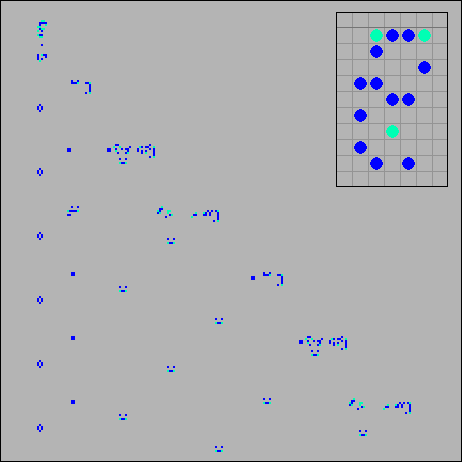
[24] Размножитель типа MMM
Эмерсон Дж. Перкинс обнаружил очень интересный размножитель. По его мнению, в других известных клеточных автоматах подобное не встречается. При взаимодействии двух одинаковых поперечных граблей порождаются такие же грабли. То есть две конфигурации напрямую порождают себе подобных.
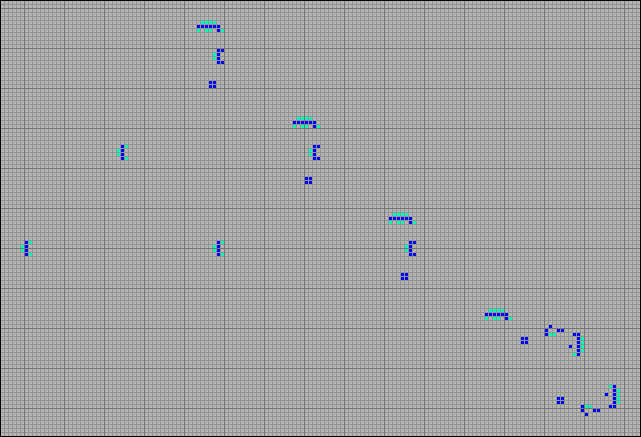
[25] Две одинаковые конфигурации порождают себе подобных
Эмерсон Дж. Перкинс сконструировал еще несколько «синтетических» размножителей. Ниже представлены размножители MMS и MMM типа. При их создании использованы элементы глайдерного синтеза, что позволяет надеяться на его возможность.
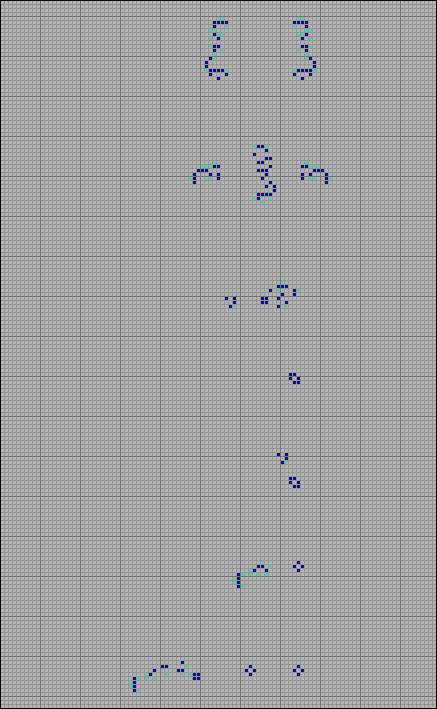
[26] MMS размножитель Перкинса

[27] MMM размножитель Перкинса
Счетчики
Существуют конфигурации, которые выпускают обратные грабли в обратном направлении. Этим конфигурациям не суждено стать размножителями, так как поток степперов от первых выпущенных обратных граблей разрушает все последующие. Не смотря на это, такие паттерны представляют определенный интерес. Дело в том, что при столкновениях вновь выпущенных обратных грабель с потоком степперов от первых обратных граблей проявляется неожиданный эффект. Каждые выпущенные обратные грабли уничтожают первый в потоке степпер, но при этом восстанавливают все уничтоженные ранее. Но именно так работает двоичный счетчик. Если рассматривать цепочку степперов как последовательность бит и, при этом, принять отсутствующий степпер за «1», а присутствующий за «0», то можно увидеть, как подсчитываются выпущенные обратные грабли

[28] Счетчик
Попробуем на основе этого паттерна создать счетчик и проверить, как он работает. Ограничимся 16-ю разрядами, то есть оставим в потоке 16 степперов. Возьмем произвольное число, например 9780. Его двоичное представление 0010011000110100. Учитывая, что период нашего счетчика равен p48, заданное количество обратных граблей будет выпущено в 9780*48=469440 поколении. Теперь сравним состояние счетчика в 0 и 469440 поколении. Можно убедиться, что счетчик работает. В последовательности степперов содержится заданное нами число.
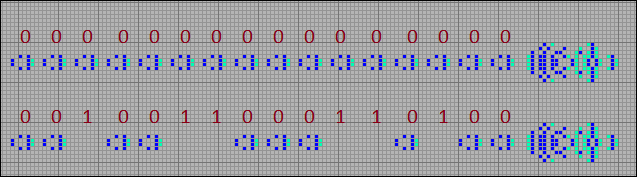
[29] Пример работы счетчика
Ружья
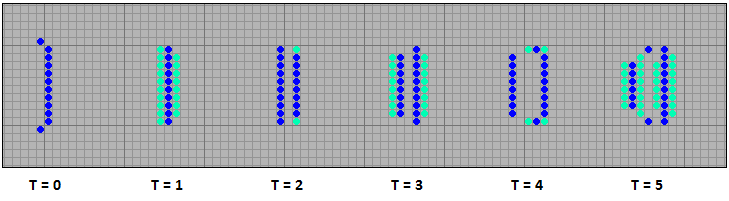
Ружьем (Gun) называют неподвижную конфигурацию, выпускающую глайдеры или космические корабли. На данный момент известно три ружья стреляющих степперами, глайдерные ружья пока не найдены. Первое из этих ружей выпускает четыре степпера шириной в четыре клетки. Его период составляет p32. На рисунке показана последовательность поколений T = 0, 6, 12, 18, 24, 32.

[30] Ружье, стреляющее степперами шириной в 4 клетки в четырех направлениях
Второе ружье имеет период p14 и выпускает четыре степпера шириной пять клеток. На рисунке показана последовательность поколений T = 0, 3, 6, 9, 12, 14.
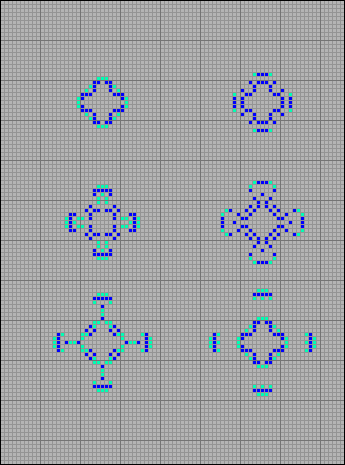
[31] Ружье, стреляющее степперами шириной в 5 клеток в четырех направлениях
И наконец, ружье, которое, как и полагается, стреляет в одну сторону. Его период p10 и оно выпускает степперы шириной шесть клеток.
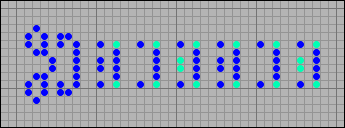
[32] Ружье, стреляющее степперами шириной в 6 клеток
Осцилляторы
Осцилляторы это неподвижные конфигурации, которые являются предшественниками самих себя. В своём развитии, они через несколько поколений возвращаются к некоторому начальному состоянию. На данный момент известно около 200 осцилляторов. Некоторые из них имеют двойников из игры Жизнь. Видно, что за счет старения клеток их период меняется в сторону увеличения. Но не у всех. Котел (Cauldron), это осциллятор в последнем ряду, в игре Жизнь имеет период p8. В Steppers его период сократился до p5.
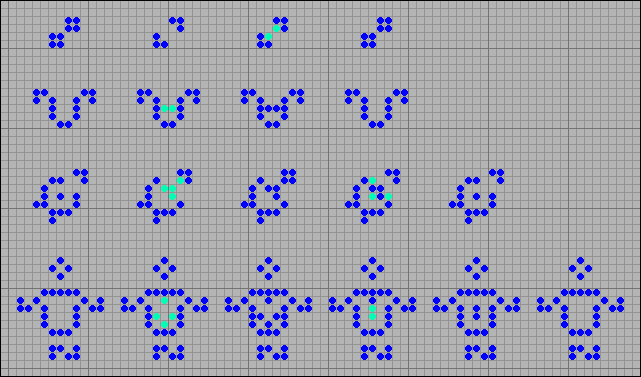
[33] Изменение периодов осцилляторов из игры Жизнь
В качестве эксперимента, большая группа осцилляторов из игры Жизнь была перенесена в клеточный автомат Steppers. Некоторые из них выжили, то есть остались осцилляторами. Ниже, показана часть из них.
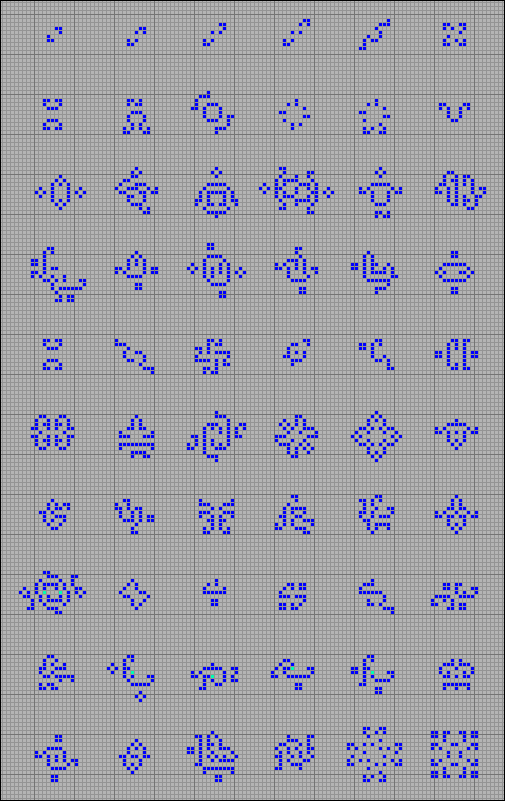
[34] Осцилляторы, существующие в игре Жизнь
Для поиска осцилляторов в Steppers был создана специальная программа, с довольно примитивным алгоритмом. В центре тороидальной решетки размером 256х256 клеток область размером 16 х 16 заполнялась ячейками со случайным состоянием. Случайным же образом выбирались 12 видов симметрии содержимого квадрата. Затем, на протяжении 500 поколений содержимое центральной области сравнивалось с 32 предыдущими состояниями. В случае если более чем период назад текущее состояние уже встречалось, её содержимое выводилось в текстовый файл. Один раз выведенные паттерны повторно уже не предъявлялись. Затем, из довольно объемного текстового файла, вручную удалось выбрать довольно интересные осцилляторы. Вот примеры некоторых из них.
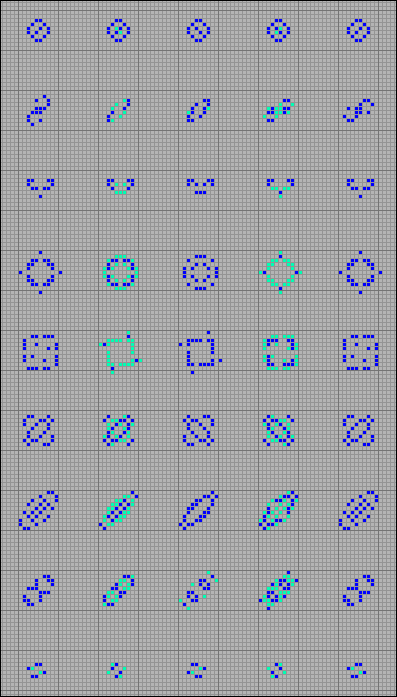
[35] Примеры осцилляторов, найденных в Steppers
А здесь почти полная коллекция известных на данный момент осцилляторов

[36] Осцилляторы клеточного автомата Steppers
Столкновения
В Steppers очень много вариантов столкновений, это связано с большим разнообразием степперов. Из-за этого, трудно сделать хоть сколько-нибудь полный обзор столкновений даже для простых степперов. Тем не менее, эксперименты показали, что при столкновениях глайдеры и степперы могут уничтожаться, рождаться, менять направление. В силу повышенной живучести клеточного автомата Steppers, часто результатом столкновений становится неудержимый рост популяции. Вероятно, это может стать препятствием для задач глайдерного синтеза и синтеза с участием степперов.
А теперь несколько примеров. Ниже показаны варианты столкновения глайдера с блоком. Как видно, результатом столкновения может быть степпер, улей (beehive) и корабль (ship). И наоборот, результатом столкновения глайдера с ульем может быть блок.

[37] Примеры столкновений глайдера с блоком
На следующей иллюстрации примеры столкновений двух простых степперов. При лобовом столкновении остается пруд, а при боковом осциллятор бакен.
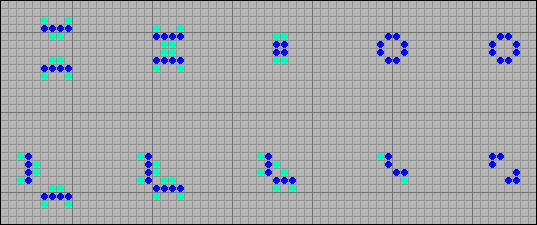
[38] Примеры столкновений двух степперов
Участник форума Conway's Game of Life Juho Pystynen (Tropylium) предложил интересные и функциональные примеры столкновений. С его разрешения публикую некоторые из них.
В первом примере сталкиваются четыре потока степперов от расходящихся обратных грабель. При нецентральном столкновении они аннигилируют, испуская четыре потока глайдеров.
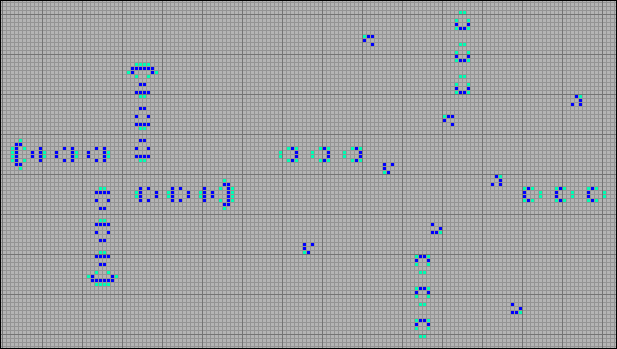
[39] Четыре потока степперов порождают глайдеры
В следующем примере семь глайдеров отражаются от двух параллельных потоков степперов, порожденных соответствующими обратными граблями. При столкновениях глайдеров с потоком степперов, формируется последовательность блоков.
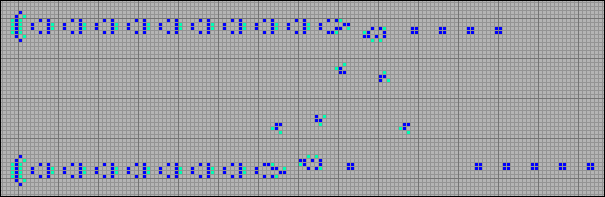
[40] Отражение глайдеров
Заключение
В статье представлены результаты довольно поверхностного изучения клеточного автомата Steppers. Многие вопросы остаются невыясненными. Например:
- Не известно, существуют ли глайдерные ружья.
- Не открыто ни одного космического корабля, который не был бы степпером или глайдером, хотя нет оснований думать, что они невозможны.
- Не найдены паровозы, оставляющие после себя осцилляторы
- Вовсе не изучены агары. Это конфигурации, покрывающие всю плоскость и периодичные в пространстве и времени.
- Не найдены пожиратели, конфигурации поглощающие глайдеры или степперы без ущерба для себя.
- Не изучен глайдерный синтез как и синтез с помощью степперов.
Надеюсь, что эти открытые вопросы привлекут любителей к исследованию клеточного автомата Steppers. Уверен, на данный момент несравненно проще сделать какое-нибудь открытие в Steppers, чем, во вдоль и поперек изученной, игре Жизнь.
Файлы для загрузки
MilhinSA.Golly2.5.zip (48.2 кб) — Правило MilhinSA и rle-файлы примеров.
Steppers-catalog.zip (221 кб) — Каталог конфигураций клеточного автомата Steppers.
SidorovI.Golly2.5.zip (18.9 кб) — Правило SidorovI c примерами.
SidorovI.Science_and_Life_1975.03.djvu (187 кб) — Статья И. Сидорова в журнале «Наука и жизнь», 1975.03.
Автор: milhinsa






