Попалась мне неплохая статья, про метод спектрального оценивания, который отлично подходит для короткого сигнала из суммы слабозашумленных гармоник. (-копия) Возможно, мои комментарии помогут читателю вникнуть в суть метода. Что немного огорчило, так это не до конца реализованные возможности метода. Метод применен для радиолокации — для быстрого определения направления на приходящие сигналы (угла θ) с последующей целью автоматической, надо понимать, адаптации системы. Но — численного определения этого угла автор не производит (причем по контексту это странно), хотя это определение вполне возможно. Имеем только красивые графики, по которым, получается, системе надо еще «ползать» и «ползать», определяя количество и расположение максимумов, что не совсем хорошо.
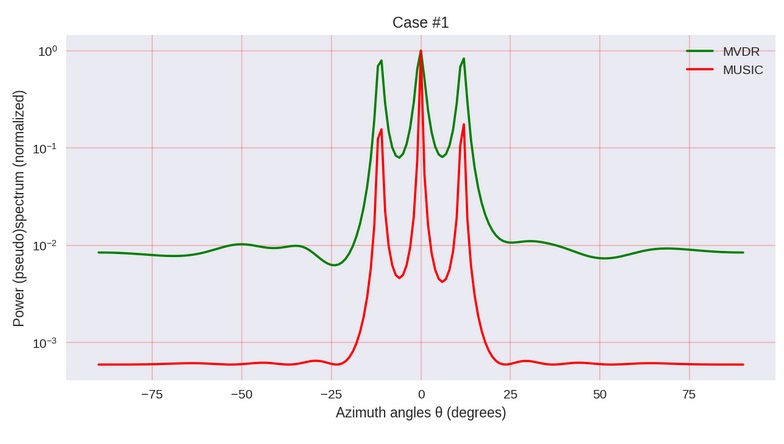
Иллюстрация автора упомянутой статьи
«Постановка задачи»
Коротко: нам надо как-то определить, откуда (под каким углом) приходит сигнал на решетчатую антенну. Чтобы потом ее подстраивать по направлению — но это уже не в этой «песне».
«Моделирование принятого сигнала»

(не суть важно — по-видимому, «символ» везде надо читать, как «сигнал»)
Здесь — осторожнее. Автор, похоже, работает с неким комплексным сигналом (пространственным). Хотя X, да, мог бы быть, как написано, матрицей «комплексных амплитуд» (зависеть не от координаты, а от пространственной частоты), но, например, XXH — это «ковариации», а не «спектральные плотности».
На матрицу «комплексных амплитуд» больше похожа S, с помощью которой моделируются гармонические составляющие (полезный сигнал). Ни аддитивные шумы, ни, похоже, даже гармонические составляющие аналитическим сигналом здесь не являются. Хотя гармоники, с оговорками, очень близки к этому.

«# Общая формула:
# sqrt(N0/2)*(G1 + jG2),
# где G1 и G2 — независимые гауссовские процессы.»
Главное — откуда из реальных замеров появится мнимая составляющая, как-то непонятно. Вычислить аналитический сигнал хоть в принципе возможно.
Не исключено, что есть «первоисточник», где работали с действительными X (принятый сигнал). Например, автор, похоже, очень стремился «сделать» получаемые спектры симметричными (четными) — во всех рассмотренных случаях тестовые сигналы заданы приходящими симметрично слева и справа.
«Условия».
Определили диапазон углов θ прихода сигнала, в котором есть смысл искать. Правда, потом графики строим всё равно почему-то от +90 до -90 град.
«Немного теории о самом методе»
Дополнение. MUSIC получается из авторегрессионного оценивания (из уравнений Юла-Уолкера) практически сам по себе, в случае, если дисперсия условного белого шума пренебрежимо мала. Результаты практически совпадают. Решение СЛАУ даже несколько экономичнее, чем поиск собственных векторов, но, кстати, по ряду соображений спектральное разложение ковариационной матрицы при ее плохой обусловленности по-любому производить бы очень желательно.
EVD, вообще-то, это просто = «нахождение собственных значений и векторов», и не более того. Не алгоритм.
Почему пишем «псевдоспектр» — потму что по одним только собственным векторам ковариационной (корреляционной) матрицы спектр можно определить только с точностью до масштабного множителя, т.е. получаемые абсолютные величины смысла не имеют. Но нам и нужно именно и только положение максимумов.

— Это самое интересное. Ну, во-первых, U0 — это уже собственные вектора, только для ковариационной матрицы — и «сэкономить» на их поиске не получится. Далее. Поиск решений приведет к необходимости определения корней степенного уравнения, что абсолютно эквивалентно еще одному спектральному разложению. Автор, по-видимому, путает собственные значения совершенно разных матриц.
Но… главное… вот теперь(!), наконец-то(!), мы смогли бы, логарифмируя корни, численно определить комплексные «импедансы» (полюса модели)(в уравнении — это опять θ, что не очень хорошо), которые нам своей мнимой частью покажут этот самый угол, под которым сигнал пришел. Вот очень жаль, что автор этого не сделал.
«Моделирование»
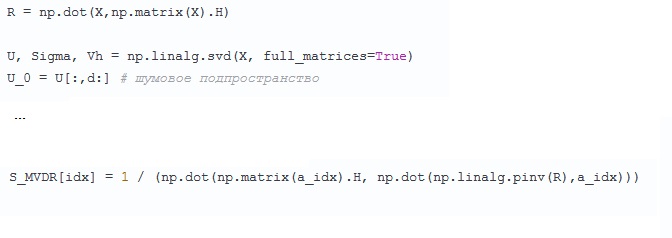
Вот немножко настораживает — сначала рассчитана матрица ковариаций R= XXH, про которую почему-то тут же на некоторое время забыли и начали все снова — раскладываем на сингулярные числа и вектора X. Обещали-то по тексту- искать собственные значения и вектора R, что, конечно, то же самое, но как бы логичнее, когда R уже нашли. Непонятно, с какой проблемой автор столкнулся.
Про R мы вспоминаем, когда оцениваем спектр по методу минимума дисперсии MVDR. И вот тут тоже интересно — R, судя по скрипту, похоже, была обращена, в полном соответствии с этим методом, классическим образом, безо всяких SVD (псевдоинверсии), хотя она, вроде как должна быть малоранговой (сильно вырожденной). В смысле, шумы у нас не такие уж маленькие? Ну, может быть.
Реально же смущает вот что. Размер «шумового подпространства» в скрипте, похоже, назначен волевым порядком (равным d). А мы же в реальном-то случае не знаем, сколько там в сигнале гармоник, а сколько — шумов. Вот надо было эти собственные значения-то проанализировать — какие из них пренебрежимо малы, какие -нет.
В целом, работа очень интересная, и не только для радиолокации. У метода, я считаю, большой потенциал, именно вот для таких типов сигнала. Автор поработал очень даже неплохо, а некоторые досадные нестыковки не так уж сложно исправить. И главное — вот дополнить бы статью методом RootMUSIC.
Автор: crowncork