Давайте создадим прототип агента обучения с подкреплением (RL), который овладеет навыком трейдинга.
Учитывая, что реализация прототипа работает на языке R, я призываю пользователей и программистов R приблизиться к идеям, изложенным в этом материале.
Это перевод моей англоязычной статьи: Can Reinforcement Learning Trade Stock? Implementation in R.
Хочу предупредить код-хантеров, что в этой заметке есть только код нейронной сети, адаптированной под R.
Если я не отличился хорошим русским языком, укажите на ошибки (текст готовился с подмогой автоматического переводчика).
Введение в проблему
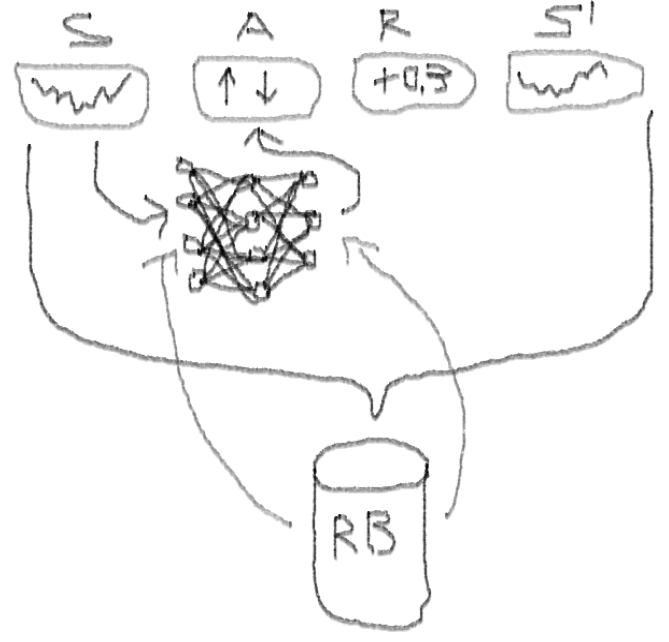
Советую начать погружение в тему с этой статьи: DeepMind
Она познакомит вас с идеей использования Deep Q-Network (DQN) для аппроксимации функции ценности, которая имеют решающее значение в Марковских процессах принятия решений.
Я также рекомендую углубиться в математику с использованием препринта этой книги Ричарда С. Саттона и Эндрю Дж. Барто: Reinforcement Learning
Ниже я представлю расширенную версию оригинального DQN, которая включает в себя больше идей, помогающих алгоритму быстро и эффективно сходиться, а именно:
Глубокие двойные дуэлирующие зушумленные нейронные сети (Deep Double Dueling Noisy NN) с приоритетной выборкой из буфера воспроизведения опыта.
Что делает этот подход лучше классического DQN?
- Двойные: есть две сети, одна из которых обучается, а другая оценивают следующие значения Q
- Дуэлирующие: есть нейроны, которые явно оценивают ценность и преимущества
- Шумные: существуют шумовые матрицы, применяемые к весам промежуточных слоев, где средние и стандартные отклонения являются обучаемыми весами
- Приоритетность выборки: батчи наблюдений из буфера воспроизведения содержат примеры, из-за которых предыдущие тренировки функций приводили к большим остаткам, которые можно сохранить во вспомогательном массиве.
Ну, а как насчет торговли, совершенной агентом DQN? Это интересная тема как таковая
Есть причины, почему это интересно:
- Абсолютная свобода выбора представлений состояния, действий, наград и архитектуры NN. Можно обогатить пространство входов всем, что вы считаете достойным попробовать, от новостей до других акций и индексов.
- Соответствие торговой логики логике обучения подкрепления в том, что: агент совершает дискретные (или непрерывные) действия, вознаграждается редко (после закрытия сделки или истечения периода ), среда частично наблюдаема и может содержать информацию о следующих шагах, торговля является эпизодической игрой.
- Можно сравнивать результаты DQN с несколькими эталонами, такими как индексы и технические торговые системы.
- Агент может непрерывно изучать новую информацию и, таким образом, приспосабливаться к изменяющимся правилам игры.
Чтобы не растягивать материал, посмотрите код этой NN, которым я хочу поделиться, поскольку это одна из загадочных частей всего проекта.
R-код для ценностной нейронной сети, использующей Keras для построения нашего агента RL
# configure critic NN ------------
library('keras')
library('R6')
learning_rate <- 1e-3
state_names_length <- 12 # just for example
a_CustomLayer <- R6::R6Class(
"CustomLayer"
, inherit = KerasLayer
, public = list(
call = function(x, mask = NULL) {
x - k_mean(x, axis = 2, keepdims = T)
}
)
)
a_normalize_layer <- function(object) {
create_layer(a_CustomLayer, object, list(name = 'a_normalize_layer'))
}
v_CustomLayer <- R6::R6Class(
"CustomLayer"
, inherit = KerasLayer
, public = list(
call = function(x, mask = NULL) {
k_concatenate(list(x, x, x), axis = 2)
}
, compute_output_shape = function(input_shape) {
output_shape = input_shape
output_shape[[2]] <- input_shape[[2]] * 3L
output_shape
}
)
)
v_normalize_layer <- function(object) {
create_layer(v_CustomLayer, object, list(name = 'v_normalize_layer'))
}
noise_CustomLayer <- R6::R6Class(
"CustomLayer"
, inherit = KerasLayer
, lock_objects = FALSE
, public = list(
initialize = function(output_dim) {
self$output_dim <- output_dim
}
, build = function(input_shape) {
self$input_dim <- input_shape[[2]]
sqr_inputs <- self$input_dim ** (1/2)
self$sigma_initializer <- initializer_constant(.5 / sqr_inputs)
self$mu_initializer <- initializer_random_uniform(minval = (-1 / sqr_inputs), maxval = (1 / sqr_inputs))
self$mu_weight <- self$add_weight(
name = 'mu_weight',
shape = list(self$input_dim, self$output_dim),
initializer = self$mu_initializer,
trainable = TRUE
)
self$sigma_weight <- self$add_weight(
name = 'sigma_weight',
shape = list(self$input_dim, self$output_dim),
initializer = self$sigma_initializer,
trainable = TRUE
)
self$mu_bias <- self$add_weight(
name = 'mu_bias',
shape = list(self$output_dim),
initializer = self$mu_initializer,
trainable = TRUE
)
self$sigma_bias <- self$add_weight(
name = 'sigma_bias',
shape = list(self$output_dim),
initializer = self$sigma_initializer,
trainable = TRUE
)
}
, call = function(x, mask = NULL) {
#sample from noise distribution
e_i = k_random_normal(shape = list(self$input_dim, self$output_dim))
e_j = k_random_normal(shape = list(self$output_dim))
#We use the factorized Gaussian noise variant from Section 3 of Fortunato et al.
eW = k_sign(e_i) * (k_sqrt(k_abs(e_i))) * k_sign(e_j) * (k_sqrt(k_abs(e_j)))
eB = k_sign(e_j) * (k_abs(e_j) ** (1/2))
#See section 3 of Fortunato et al.
noise_injected_weights = k_dot(x, self$mu_weight + (self$sigma_weight * eW))
noise_injected_bias = self$mu_bias + (self$sigma_bias * eB)
output = k_bias_add(noise_injected_weights, noise_injected_bias)
output
}
, compute_output_shape = function(input_shape) {
output_shape <- input_shape
output_shape[[2]] <- self$output_dim
output_shape
}
)
)
noise_add_layer <- function(object, output_dim) {
create_layer(
noise_CustomLayer
, object
, list(
name = 'noise_add_layer'
, output_dim = as.integer(output_dim)
, trainable = T
)
)
}
critic_input <- layer_input(
shape = c(as.integer(state_names_length))
, name = 'critic_input'
)
common_layer_dense_1 <- layer_dense(
units = 20
, activation = "tanh"
)
critic_layer_dense_v_1 <- layer_dense(
units = 10
, activation = "tanh"
)
critic_layer_dense_v_2 <- layer_dense(
units = 5
, activation = "tanh"
)
critic_layer_dense_v_3 <- layer_dense(
units = 1
, name = 'critic_layer_dense_v_3'
)
critic_layer_dense_a_1 <- layer_dense(
units = 10
, activation = "tanh"
)
# critic_layer_dense_a_2 <- layer_dense(
# units = 5
# , activation = "tanh"
# )
critic_layer_dense_a_3 <- layer_dense(
units = length(acts)
, name = 'critic_layer_dense_a_3'
)
critic_model_v <-
critic_input %>%
common_layer_dense_1 %>%
critic_layer_dense_v_1 %>%
critic_layer_dense_v_2 %>%
critic_layer_dense_v_3 %>%
v_normalize_layer
critic_model_a <-
critic_input %>%
common_layer_dense_1 %>%
critic_layer_dense_a_1 %>%
#critic_layer_dense_a_2 %>%
noise_add_layer(output_dim = 5) %>%
critic_layer_dense_a_3 %>%
a_normalize_layer
critic_output <-
layer_add(
list(
critic_model_v
, critic_model_a
)
, name = 'critic_output'
)
critic_model_1 <- keras_model(
inputs = critic_input
, outputs = critic_output
)
critic_optimizer = optimizer_adam(lr = learning_rate)
keras::compile(
critic_model_1
, optimizer = critic_optimizer
, loss = 'mse'
, metrics = 'mse'
)
train.x <- rnorm(state_names_length * 10)
train.x <- array(train.x, dim = c(10, state_names_length))
predict(critic_model_1, train.x)
layer_name <- 'noise_add_layer'
intermediate_layer_model <- keras_model(inputs = critic_model_1$input, outputs = get_layer(critic_model_1, layer_name)$output)
predict(intermediate_layer_model, train.x)[1,]
critic_model_2 <- critic_model_1
Я использовал этот источник, чтобы адаптировать код Python для шумовой части сети: github repo
Эта нейронная сеть выглядит так:
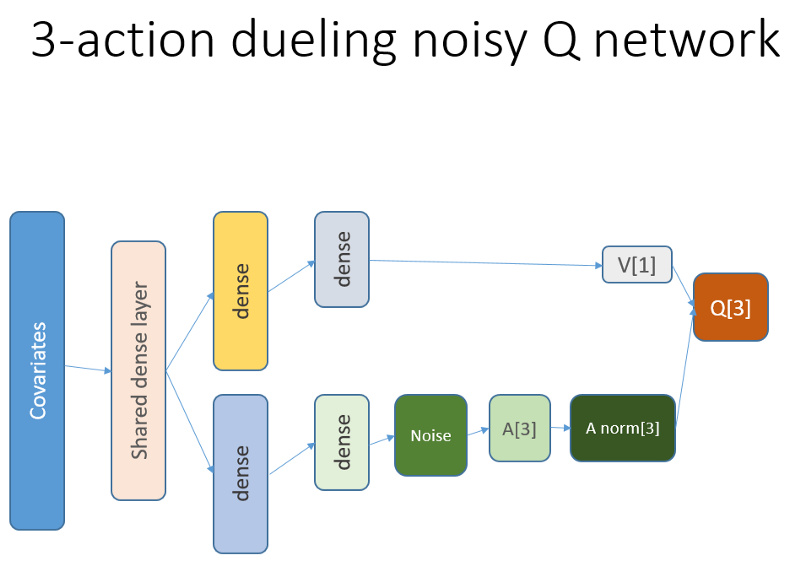
Напомним, что в дуэльной архитектуре мы используем равенство (уравнение 1):
Q = A '+ V, где
A '= A — avg (A);
Q = ценность состояния-действия;
V = ценность состояния;
А = преимущество.
Другие переменные в коде говорят сами за себя. Кроме того, эта архитектура хороша только для определенной задачи, поэтому не принимайте ее как должное.
Остальная часть кода, скорее всего, будет достаточно шаблонной для публикации, а для программиста будет интересно написать ее самостоятельно.
А теперь — эксперименты. Тестирование работы агента производилось в песочнице, далекой от реалий торговли на живом рынке, у настоящего брокера.
Фаза I
Мы запускаем нашего агента против синтетического набора данных. Наша стоимость транзакции равна 0,5:
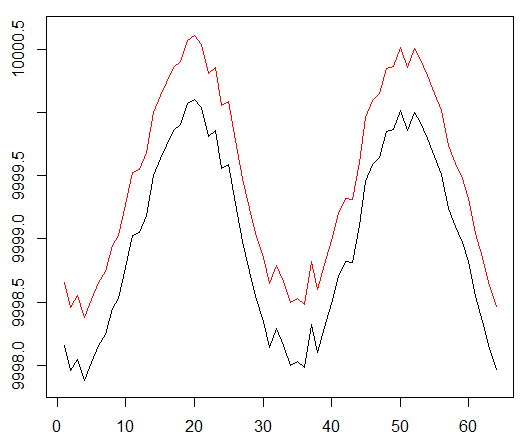
Результат отличный. Максимальное среднее эпизодическое вознаграждение в этом эксперименте
должно быть 1,5.
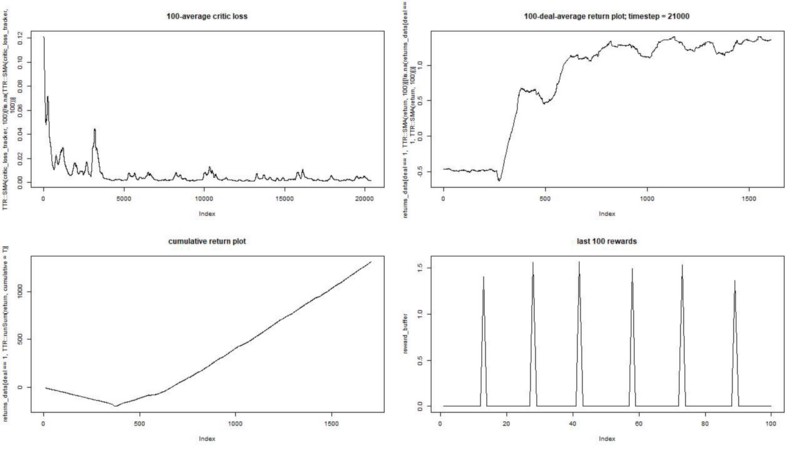
Мы видим: потери критика (так еще называют сеть ценности в подходе актор-критик), среднее вознаграждение за эпизод, накопленное вознаграждение, выборка последних вознаграждений.
Фаза II
Мы обучаем нашего агента произвольно выбранному биржевому символу, который демонстрирует интересное поведение: ровное начало, быстрый рост в середине и тоскливый конец. В нашем тренировочном наборе около 4300 дней. Стоимость транзакции установлена на уровне 0,1 доллара США (целенаправленно низкая); наградой является USD Прибыль / убыток после закрытия сделки на покупку / продажу 1.0 акции.
Источник: finance.yahoo.com/quote/algn?ltr=1
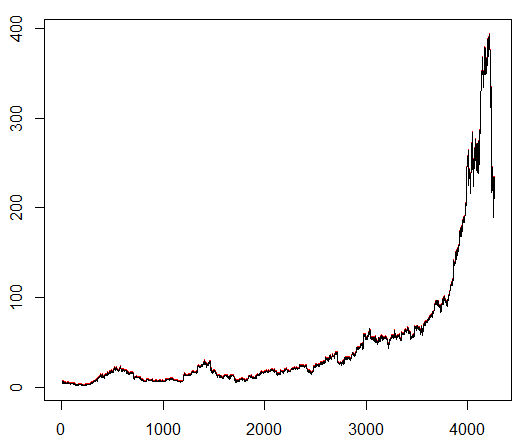
NASDAQ: ALGN
После настройки некоторых параметров (оставив архитектуру NN такой же) мы пришли к такому результату:
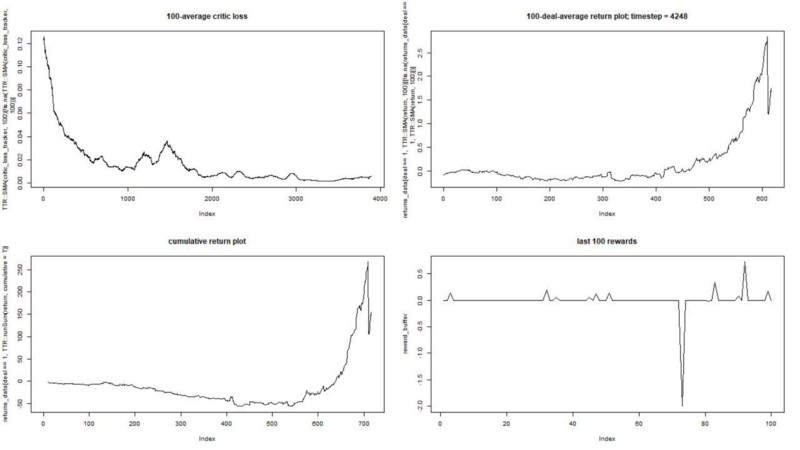
Получилось не плохо, так как в конце концов агент научился получать прибыль, нажимая три кнопки на своей консоли.
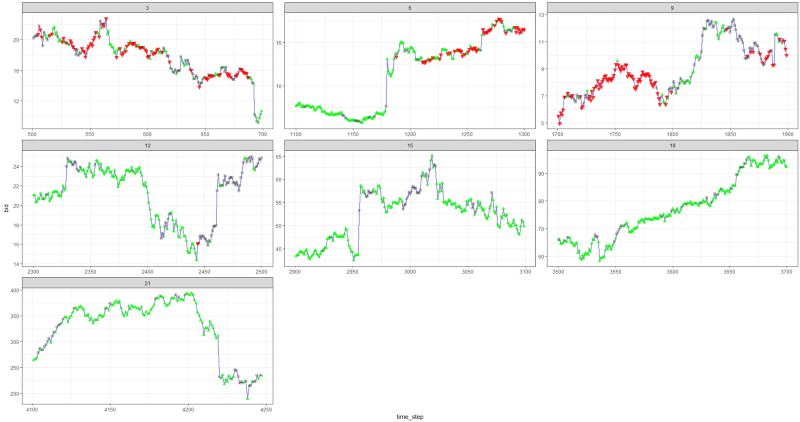
красный маркер = продать, зеленый маркер = купить, серый маркер = ничего не делать.
Обратите внимание, что на его вершине среднее вознаграждение за эпизод превысило реалистическую стоимость транзакции, с которой можно столкнуться в реальной торговле.
Жаль, что акции падают как сумасшедшие из-за плохих новостей…
Заключительные замечания
Торговать с помощью RL не только сложно, но и полезно. Когда ваш робот делает это лучше, чем вы, пришло время тратить личное время, чтобы получить образование и здоровье.
Я надеюсь, что это было интересное путешествие для вас. Если вам понравилась эта история, помашите рукой. Если будет много интереса, я могу продолжить и показать вам, как методы градиента политики (policy gradient) работают с использованием языка R и API Keras.
Я также хочу поблагодарить моих друзей, увлеченных нейронными сетями, за советы.
Если у вас остались вопросы — я всегда здесь.
Автор: Alexey_mosc






