Когда-то давно друзья подарили вот такую головоломку:

Собрать её самостоятельно я так и не смог (всегда оставался один фрагмент). Посему было решено написать программу.
Для тех, кто не любит читать, решение доступно по ссылке (внимание, сильно нагружает процессор).
Итак, имеем головоломку, состоящую из 25 одинаковых элементов, которые необходимо уложить в куб 5х5х5, где за единицу измерения взято наименьшее ребро элемента.
Выбор языка пал на JavaScript. Принеся в жертву производительность ради визуализации (очень уж хотелось сделать визуализированный брутфорс, как в кино), благо процесс перебора не обещался быть слишком продолжительным (почему, будет написано ниже).
Основной процесс сборки будет происходить в трехмерном целочисленном массиве (5х5х5), назовем его «коробок», где неотрицательным значением будем обозначать ячейку, занятую кубиком элемента. Для большей информативности этим значением будет порядковый номер положения элемента в трехмерном пространстве. Всего существует 24 положения элемента в трехмерном пространстве, если угол поворота вокруг каждой оси кратен 90°. Для простоты подсчета числа положений я представил кубик рубика, у которого грани окрашены разными цветами. Каждый раз он обращается к нам новой гранью и поворачивается четыре раза по часовой стрелке на 90° таким образом, чтобы эта грань всегда смотрела на нас. Итого 6 граней х 4 поворота = 24 положения в пространстве, где наши глаза неподвижны.
Зная число положений объекта в трехмерном пространстве и дополнив его отражением каждого состояния (другие два отражения как совместно так и по отдельности дадут либо тот же куб либо его первое отражение после кручения), получим, что на каждое уникальное решение головоломки, которых может быть больше одного, приходится еще 47 его вариаций, а следовательно, время, требуемое для решения, будет меньше времени полного перебора. К сожалению, формулу расчета числа ходов для нахождения решения вывести не смогу, поэтому если кто-нибудь может, напишите, пожалуйста, в комментариях, добавлю в статью.
Положение элемента в пространстве будет представлять собой относительные координаты пяти единичных кубиков, из которых состоит элемент: координаты будут браться относительно базовой точки (ее координаты [0,0,0], соответственно). Основным условием расположения базовой точки является ее обязательное нахождение на элементе таким образом, что при заполнении этим элементом куба, базовая точка располагалась на базовом уровне куба. Под базовым уровнем будем понимать уровень по оси Z, на котором в данный момент происходит сборка (уровни ниже заполнены полностью). Таким образом мы упростили себе (и не только) дальнейшие расчеты.
//x,y,z
var elems=[
[[0,0,0],[1,0,0],[1,1,0],[2,1,0],[3,1,0]],//0
[[0,0,0],[1,0,0],[2,0,0],[0,0,1],[-1,0,1]],//1
[[0,0,0],[1,0,0],[1,-1,0],[2,-1,0],[3,-1,0]],//2
[[0,0,0],[1,0,0],[1,0,1],[2,0,1],[3,0,1]],//3
[[0,0,0],[1,0,0],[2,0,0],[2,-1,0],[3,-1,0]],//4
[[0,0,0],[1,0,0],[2,0,0],[2,0,1],[3,0,1]],//5
[[0,0,0],[1,0,0],[2,0,0],[2,1,0],[3,1,0]],//6
[[0,0,0],[1,0,0],[0,0,1],[-1,0,1],[-2,0,1]],//7
[[0,0,0],[0,1,0],[1,1,0],[1,2,0],[1,3,0]],//8
[[0,0,0],[0,1,0],[0,1,1],[0,2,1],[0,3,1]],//9
[[0,0,0],[0,1,0],[-1,1,0],[-1,2,0],[-1,3,0]],//10
[[0,0,0],[0,1,0],[0,2,0],[0,0,1],[0,-1,1]],//11
[[0,0,0],[0,1,0],[0,2,0],[-1,2,0],[-1,3,0]],//12
[[0,0,0],[0,1,0],[0,0,1],[0,-1,1],[0,-2,1]],//13
[[0,0,0],[0,1,0],[0,2,0],[1,2,0],[1,3,0]],//14
[[0,0,0],[0,1,0],[0,2,0],[0,2,1],[0,3,1]],//15
[[0,0,0],[0,0,1],[0,0,2],[0,1,2],[0,1,3]],//16
[[0,0,0],[0,0,1],[0,0,2],[-1,0,2],[-1,0,3]],//17
[[0,0,0],[0,0,1],[0,0,2],[0,-1,2],[0,-1,3]],//18
[[0,0,0],[0,0,1],[0,0,2],[1,0,2],[1,0,3]],//19
[[0,0,0],[0,0,1],[0,1,1],[0,1,2],[0,1,3]],//20
[[0,0,0],[0,0,1],[-1,0,1],[-1,0,2],[-1,0,3]],//21
[[0,0,0],[0,0,1],[0,-1,1],[0,-1,2],[0,-1,3]],//22
[[0,0,0],[0,0,1],[1,0,1],[1,0,2],[1,0,3]]//23
];
Порядок сборки определяется самой головоломкой: собираем снизу вверх, как только уровень заполняется полностью, переходим к следующему. Порядок брутфорса определяется массивом положений элементов в пространстве. Если после частичного заполнения уровня для какой-то свободной точки невозможно подобрать положение, предыдущий найденный элемент считается неверным, удаляется из массива текущего состояния и «коробка», продолжается поиск.
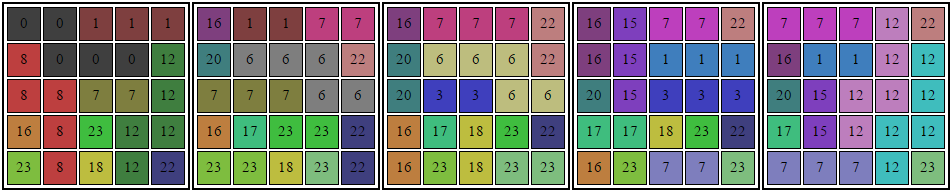
Что касается визуализации, трехмерное представление куба выполним в виде пяти срезов по оси Z, по срезу на каждый уровень.
Срезы представляют собой таблицы 5х5, заполненные ячейками с неотрицательными номерами из «коробка». Ячейки дополнительно окрашены разными цветами для отделения элементов головоломки друг от друга. Для снижения нагрузки состояние массива будем отображать раз в секунду или в критические моменты: запуск, пауза, остановка при нахождении ответа. Дополнительно для работы будем использовать «строку сохранения», с помощью которой можно ставить на паузу, вносить изменения в код и продолжать поиск с места паузы, а не с начала. Так же, отобразим число циклов (за момент окончания цикла примем момент отображения текущего состояния массива), число «переборов» за последний цикл и общее число «переборов».
Из особенностей стоит отметить, что в предстартовой подготовке в начале создается массив возможных положений для каждой координаты «коробка», чтобы заранее отсечь положения, которые не могут располагаться в этой точке. Так же для универсальности добавил возможность менять значения размера «коробка» по все трем координатам. Для увеличения скорости визуализации добавил массив ячеек таблиц срезов.
Полный код с комментариями:
— GitHub
— JSFiddle
Запускаем, ждем (у меня ушло 114 циклов на Google Chrome, перебрав 96969659 вариантов), смотрим ответ и собираем уже в реальной жизни.
Автор: CnapoB






