Большинство сложных задач с данными требуют немалого количества ресурсов. Поэтому почти у каждого дата-центра в мире не один, а множество клиентов — даже если все они выступают под общим брендом. Компаниям нужны мощности под самые разные сервисы и цели, да и в процессе достижения какой-нибудь одной из них приходится иметь дело с целым набором подзадач. Как дата-центру справиться с потоком желающих что-нибудь проанализировать или посчитать? Поступающие заказы на вычисления нужно выполнять в некотором порядке, стараясь никого не обделить ресурсами. Эта лекция — об основных методах распределения реальных задач на большом кластере. Способ, о котором рассказал Игнат Колесниченко, применяется для обслуживания почти всех сервисов Яндекса.
Игнат — руководитель одной из групп в нашей службе технологий распределенных вычислений. Окончил мехмат МГУ и Школу анализа данных, в Яндексе с 2009 года.
Под катом — подробная расшифровка лекции и слайды.
Всем добрый вечер. Меня зовут Колесниченко Игнат, я работаю в Яндексе, в службе распределенных технологий и вычислений. И сегодня я вам попробую рассказать про одну задачу, которую я встретил во вполне реальной жизни. Для начала давайте чуть побольше расскажу о том, из чего состоит моя работа, что мы делаем. А дальше — чуть подробнее о деталях, и перейдем в итоге к задаче, поймем, в чем она состоит.
Что за продукт мы делаем? Мы делаем продукт для разработчиков и аналитиков Яндекса. Задача состоит в том, что мы строим большие кластера и софт поверх них. Эти большие кластера и софт поверх них позволяют хранить огромные объемы данных, и не только хранить их, но и обрабатывать. Под огромными объемами я подразумеваю петабайты, десятки петабайт. Петабайт в тысячу раз больше терабайта, а десятки тысяч петабайт больше в десятки тысяч раз. Задача в том, чтобы построить такую систему, в которую обычные разработчики и аналитики Яндекса могли бы прийти, запустить там свой достаточно простой код, и он бы быстро и распределенно на всем кластере отработал, получил бы результат. Затем они построили бы какой-нибудь свой график, поняли, что доля Яндекса растет или падает и делали бы уже какие-то выводы, улучшали свой софт.
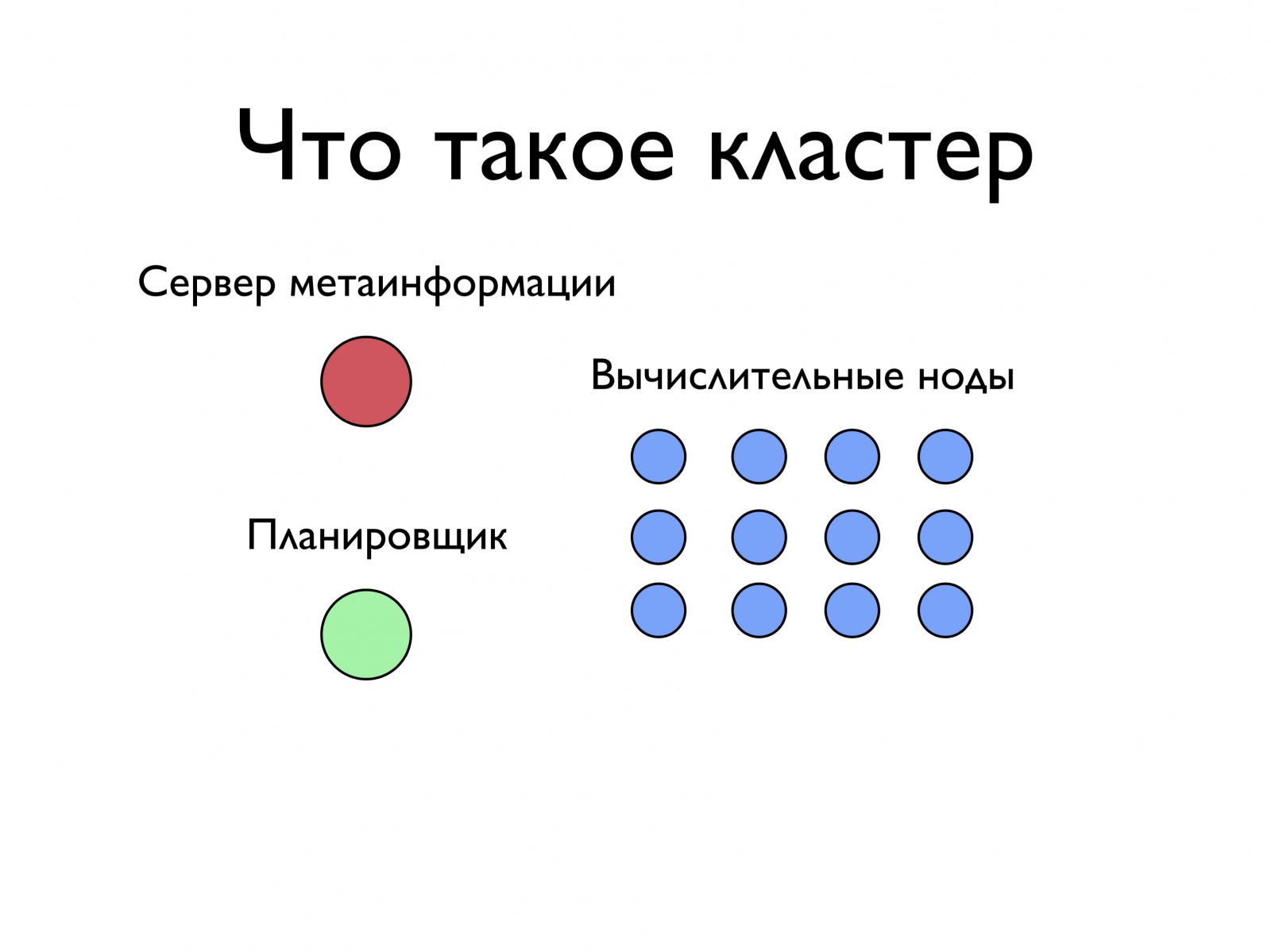
Что из себя представляет кластер в нашем случае? В нашем случае кластер очень упрощенно выглядит следующим образом. Это много-много серверов, которые называются вычислительными нодами. Сервер — это в целом то же самое, что и ваш ноутбук, только гораздо более мощный, и стоит он не где-то, а в дата-центре в какой-то полке. Типичные характеристики у сервера — не как в обычных ноутбуках, где 4-8 ядер. У них 30 ядер, 128 Гбайт памяти, в общем, много ресурсов, которые можно использовать для того, чтобы запускать задачи.
Кроме того, чтобы этими вычислительными нодами управлять, чтобы что-то там запускать, чтобы что-то работало, чтобы хранить данные, нужна некоторая система. И важной частью системы являются две вещи — сервер метаинформации, который будет знать, где какие данные в этом кластере лежат и что на нем происходит, и планировщик, который будет решать, где какие задачи запускать. Мы сегодня будем по большей части разговаривать про планировщик. Давайте чуть детальнее посмотрим, что он может из себя представлять.
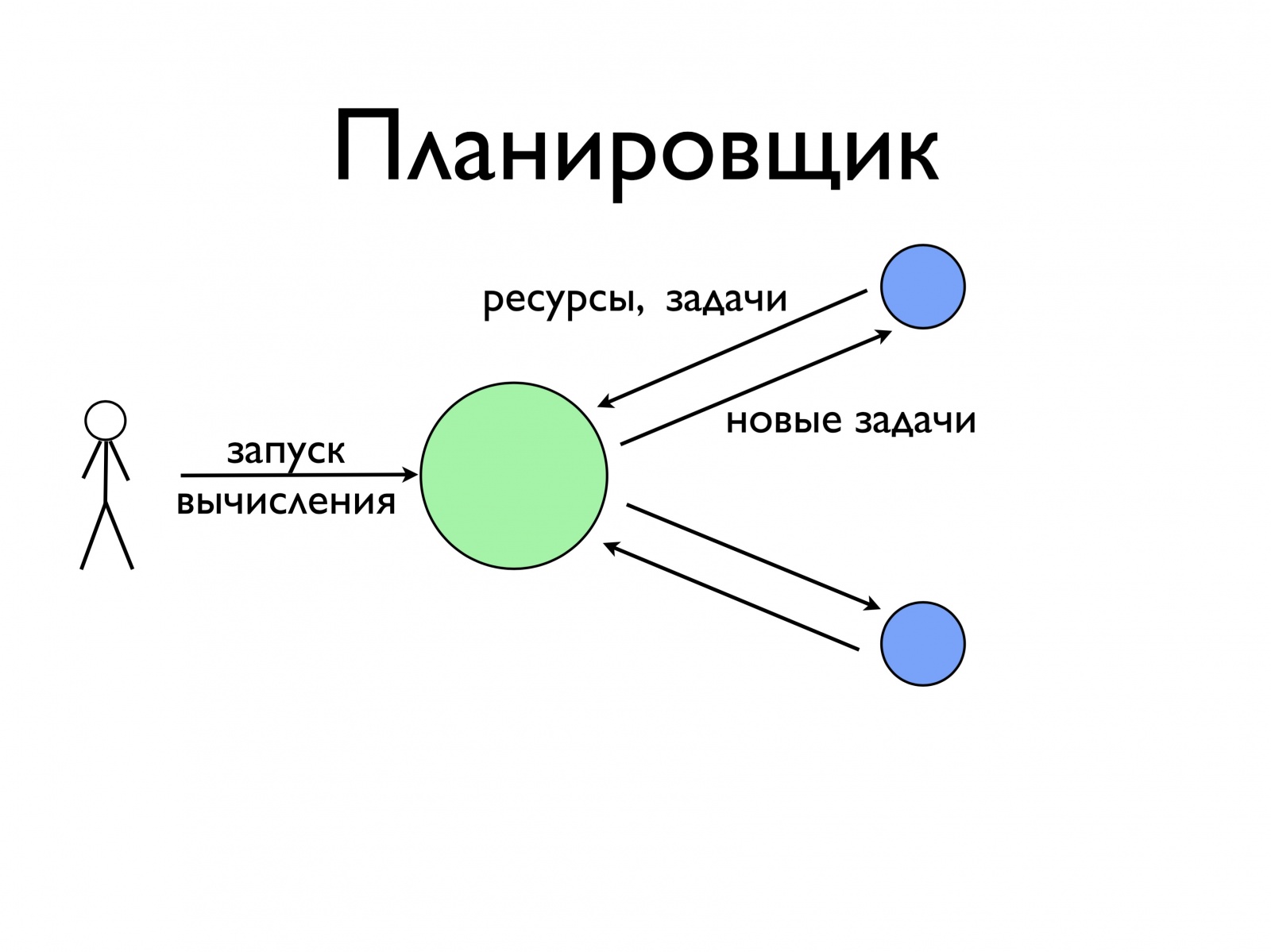
Планировщик по факту представляет из себя сервер или, может быть, несколько серверов. А с точки зрения интерфейса — того, как с ним работают пользователи и как он общается с внешним миром, — у него есть два вида общения. Один вид — это запуск вычислений, когда приходит разработчик и говорит серверу в некотором виде запустить написанную им программу. Дальше планировщик говорит: «Да, я вашу программу принял, запустил. Теперь вот здесь вы можете смотреть, что с ней произойдет, когда она выполнится или не выполнится». Кроме того, он общается с нашими вычислительными нодами, с серверами. Что ему сообщают вычислительные ноды? Вычислительные ноды говорят: «Смотри, у меня есть столько-то свободных ресурсов, у меня половина CPU не занято, куча свободной памяти, это все не используется. Дай мне какое-нибудь задание», — на что планировщик отвечает: «О! Держи новые задачи». И так каждая нода с этим одним-единственным планировщиком общается.

Еще детальнее это выглядит примерно следующим образом. У планировщика должна быть некоторая стратегия того, как он решает, какие задачи запускать, когда они к нему приходят, и на каких нодах. Пользователь приходит и запускает свои вычисления. Планировщик запоминает: «О, у меня есть такое-то вычисление» — и где-то их хранит в своей внутренней структуре данных. Кроме того, у него есть некоторая своя стратегия. И когда вычислительная нода к нему приходит, сообщает ему про те задачи и ресурсы, которые у нее бегут, наша стратегия должна ответить, что именно ноде надо сделать с ее задачами или какие запустить новые задачи. Например, она может сказать: «Запусти мне, пожалуйста, две задачи моего первого вычисления». Может сказать: «Запусти одну задачу второго вычисления, а еще оборви одну задачу третьего вычисления, потому что третье вычисление слишком много всего делает. Хватит ему это делать».
Теперь чуть подробнее про вычисления и задачи, про то, что все это из себя представляет. Ответ зависит от типа вычисления, но в простом случае можно сказать, что пользователь приходит с каким-то своим написанным кодом, будь то бинарник на Python или на С++, говорит, какие ресурсы он хочет иметь на кластере и как-то это описывает. Стратегия это как-то запоминает и те данные, которые хочется обработать, — а они лежат на разных нодах, — распределяет на кусочки. И уже на этих кусочках стратегия запускает вычисление. Мы будем считать, что каждое вычисление — их по-другому еще называют операциями — состоит просто из какого-то набора задач. Чуть дальше мы увидим, что под этим подразумевается.

Я хочу рассказать про то, что мы на предыдущем слайде называли стратегией: что это такое, какие они бывают, какими свойствами они должны обладать, как они должны работать.
Что должна делать стратегия? Ее важная функция — решить, какую задачу запустить. У нее есть много разных вычислений, которые заказали пользователи, и ей надо понять, задачу какого из этих вычислений, какой из этих операций надо запустить. Еще важно понять, чего пользователи хотят от системы. Очевидно, что пользователи запускают свои вычисления и хотят каких-то гарантий — хотят, чтобы вычисление завершилось и как можно скорее. О том, что будет подразумеваться под «как можно скорее», мы позже поговорим. И глобальный вопрос – какими свойствами должна обладать стратегия?
Прежде чем мы будем говорить про стратегию, еще нужно вспомнить про ресурсы. Это важный constraint того, как мы будем определять, что запускать, какие есть ресурсы. Два наиболее понятных и базовых ресурса — оперативная память, доступная нам на нодах, и количество процессоров. Как мы поймем, можно ли запустить какую-нибудь задачу на каком-нибудь ноде? Когда пользователь запустил вычисление, он должен нам сообщить, сколько оно съедает оперативной памяти и сколько CPU он собирается использовать. Если он не сообщил, то надо считать, что это дефолтное значение. Если реальная задача пользователя вдруг съедает больше, чем он заказал, — нужно будет просто ее убивать и говорить пользователю: «Ты запустил невалидное вычисление. Не надо так делать. Пойди поменяй свои ограничения». Но будем считать, что пользователь знает, сколько его программа съедает CPU, оперативной памяти, и исходя из этого будем действовать.
Про CPU понятно, что любая программа пользователя съедает одно CPU, потому что если приложение однопоточное — а большинство людей пишут однопоточные приложения, — то это одно CPU. А про память уже более сложный вопрос: надо понять, сколько разных структур данных программа пользователя выделит, сколько она будет есть этой памяти. И задача пользователя — понять, сколько же его программа потребляет.
Бывают менее популярные ресурсы, например интенсивность использования сети. Может случиться так, что программа пользователя ходит куда-нибудь по сети и что-нибудь себе скачивает. Бывают программы пользователя, которые активно мучают диски. Если вы начнете постоянно читать из случайных мест с вашего жесткого диска на машинке, то жесткий диск быстро закончится и перестанет вам отвечать за какое-то разумное время. Так что это тоже важно учитывать. Если запустить много задач, все из которых хотят диск на одной машинке, то все они будут работать очень медленно, а пользователю, очевидно, не этого хочется.
Нам пользователь сообщает, сколько разных ресурсов хочет каждое вычисление. И про ноды мы тоже знаем, сколько ресурсов на них есть. Можно пойти в какой-нибудь Sysprog и узнать, сколько там памяти, сколько есть свободных ядер и как сейчас используются ресурсы на нашем вычислительном сервере.

Дальше мы начнем говорить про стратегии. И первая стратегия, совершенно простая, про которую я расскажу — это стратегия FIFO. Давайте я нарисую, как она будет устроена.
Наш планировщик будет наши операции выстраивать в некоторую очередь. FIFO расшифровывается как first input first output, просто обозначая понятие очереди. Допустим, у нас были пользователи, они как-то запускали операции и у нашего планировщика есть некоторая очередь операций. Дальше все, что надо решить нашей стратегии, когда пришла наша нода с какими-то своими ресурсами, — это какие задачи каких из этих операций ей запустить. Давайте сейчас введем какие-нибудь приземленные числа — знания про наши ноды, наши операции, — и рассмотрим исходя из них конкретный пример того, как работает стратегия FIFO. Тогда будет понятно, как она устроена.
Пусть на нашей ноде 32 CPU и 63 Гбайт памяти. Первая операция пусть состоит из 1000 подзадач, и каждая подзадача пусть съедает 1 CPU и 4 Гбайт памяти. Это первая задача.
Вторая задача пусть будет совершенно другая — состоящая из 500 подзадач, каждая из которых требует, например, 10 CPU и 1 Гбайт памяти. И так далее.
Пришли пользователи, позапускали такие операции, и нашей стратегии надо понять, какую из них этой ноде дать. Допустим, к стратегии пришла свободная нода, и ей надо решить, что с ней делать.
Стратегия FIFO будет действовать следующим простым образом. Они недаром нарисованы друг за другом. Это означает, что они упорядочены по времени. Кто раньше пришел, запустил операцию — у того она первая в очереди и встала. Стратегия FIFO будет сначала предлагать первой операции: «Первая операция, есть у тебя еще какая-нибудь задача, которую я могу запустить на ноде?». Если есть, то он будет говорить ноде запустить задачу первой операции. К чему это все приведет?
Давайте еще, кроме того, предположим, что у нас таких нод 100 штук. Если у нас 100 штук нод, сколько всего ресурсов в кластере у нас сейчас есть?
— 3200 CPU и 6400 ГБ, то есть 6 с половиной ТБ.
— Да. И стратегия будет первым делом запускать все у первой операции. Несложно заметить, что в какой-то момент у этой первой операции она все запустит, а все ресурсы еще не исчерпает. То есть в какой-то момент мы придем к тому, что здесь у нас уже запущена тысяча из тысячи задач, а ресурсы еще не исчерпались, на нодах еще что-то есть. В этот момент стратегия пойдет такая: «Ага, у меня еще есть свободные ресурсы. Надо что-нибудь еще запустить». Она пойдет к следующей операции, и начнет запускать ее задачи. Можно даже понять, сколько задач второй операции ей удастся запустить в лучшем случае.
Давайте мы прикинем. Запустив первую операцию, мы потратим 1000 CPU и 4000 Гбайт памяти. Значит, у нас останется 2200 CPU и 2400 Гбайт памяти. Дальше на эти оставшиеся ресурсы она будет запускать вторую операцию. Тут главным страдающим ресурсом будет CPU, то есть его будет не хватать, потому что памяти она хочет мало, а CPU — много. Поэтому, видимо, нам удастся запустить 220 задач второй операции. И на этом стадия запуска задач закончится до тех пор, пока какие-нибудь задачи наших операций не начнут заканчиваться. Как только задачи у первой или у второй операции начнут заканчиваться, планировщик начнет это учитывать. То есть когда нода к нему приходит, она сообщает, не только какие у нее сейчас есть свободные ресурсы, а и какой статус у тех задач, которые на ней уже были запущены. Она сообщит про какие-то задачи, что они закончились. Планировщик такой: «Ага, они закончились! Можно туда пойти и что-нибудь еще спланировать». Он будет идти и пытаться смотреть на вторую операцию, чтобы что-нибудь спланировать, на третью операцию, чтобы что-нибудь спланировать.
Про 220 задач второй операции здесь есть некоторый обман. Все ли видят, в чем этот обман состоит? Почему не всегда может получиться запустить 220 задач второй операции?
— В смысле, должно получиться меньше?
— Может в некотором случае получиться меньше. Я надеюсь, что больше мы в принципе не сможем, потому что это противоречит нашим ограничениям, но может получиться по некоторым причинам меньше.
— Потому что куда-то еще уходит память.
— У нас честные ограничения, реально мы ничто больше и не тратим. Но проблема состоит в том, что задачи второй операции хотят 10 CPU, а может случиться так, что мы на одной ноде заняли 25 CPU первой задачей, и у нее осталось 7 свободных, а 7 свободных, очевидно, не хватает, и планировщик тогда не имеет права взять и запустить хотя бы одну задачу второй операции, потому что нет на нее достаточного количества ресурсов. То есть свободные ресурсы есть, но этих свободных ресурсов не хватает. Это проблема гранулярности, о которой мы сегодня, наверное, не будем говорить, но нужно понимать, что она есть. Вообще говоря, хороший планировщик должен это учитывать. Если он понимает, что где-то из-за гранулярности он что-то не может запустить, значит, он должен попробовать что-нибудь у первой операции, например, вытеснить. Понятно, что первая операция для него более удобная, ее проще запускать на других нодах в силу того, чтобы запустить хотя бы одну задачу второй операции.
Пойдем дальше. Хочется понять, какие у нас есть требования к стратегии. Вообще говоря, их можно написать большой список. Я сегодня рассмотрю три наиболее основных и важных. Давайте подробнее распишем, что они означают.

Честность – это непростое требование. Что под ним подразумевается? У стратегии FIFO есть такая проблема. Представьте, что у вас есть много пользователей, они все пришли, позапускали операции, и кому-то повезло, кто запустил первый. А кому-то — очень не повезло: он запустил, а первая операция оказалась очень долгой, нудной, и, на самом деле, может быть, никому не нужной, и человек по ошибке ее запустил, например. Тогда все оставшиеся будут стоять и ждать, пока эта первая операции закончится, или пользователь ее отменит, или что-нибудь с ней произойдет. Понятное дело, что пользователя кластера, наверное, такое не очень устраивает, что твой сосед пришел, раньше тебя встал в очередь, и что-то долго делает. И все, и ты ничего не можешь сделать, а тебе надо срочно отчет почитать, у тебя работа из-за этого стоит, и хочется, чтобы тебе что-нибудь гарантировали.
Что под этим будет подразумеваться? Допустим, есть у нас три пользователя: А, В и С. Эти пользователи могли как-нибудь договориться, какая доля кластера кому принадлежит. Например, они могли просто по своей важности или из каких-то других соображений договориться, что пользователю А положено 20% кластера, пользователю В положено 30% кластера, пользователю С — 50% кластера. И хочется, чтобы мы такую информацию могли как-то сообщить нашему планировщику, чтобы он это мог учесть в своей стратегии и раздавать ресурс так, что 20% кластера принадлежит пользователю А, 30% — пользователю В и 50% — пользователю С.
Когда мы об этом говорим, встает наивный вопрос: если они так поделили ресурсы, почему бы им не освободить себе три раздельных кластера, а не пытаться жить на одном? Этому есть причина. Причина состоит в следующем: хочется, чтобы им было выгоднее объединиться, чем жить по раздельности.
Почему такое может быть? Представьте, что задачи пользователя А для нашего кластера едят 1 CPU и 4 Гбайт памяти. У пользователя В это 10 CPU и 1 Гбайт памяти. Я утверждаю, что тогда им объединиться выгоднее, чем жить по раздельности.
Почему так? Представьте, что у пользователя А свои 20 машин, у пользователя В — 30 машин. Они запустили на всех своих машинах все свои ресурсы. Я рисую два столбика: первый столбик — CPU, второй — память. Я хочу понять в каждом этом столбике, насколько они будут заполнены с точки зрения ресурсов суммарно на всем кластере. При этом я напомню, что у нас на каждой машинке было 32 CPU и 64 Гбайт памяти. И, допустим, у этих операций очень много своих задач, которые они запускают, то есть они могут все ресурсы кластера съесть.
У этого пользователя А видно, например, что он память съест всю, а CPU — наполовину. У нас на машинке 64 Гбайт памяти и 32 CPU. Тогда сколько мы можем запустить на 64 Гбайт памяти? 16 таких задач. 16 задач — они, понятно, наполовину наше CPU не съедят.
Окей, как у второго пользователя обстоят дела? Противоположным образом. Он хочет много CPU и мало памяти. Он, видимо, съест всё CPU и сколько-то там памяти.
Дальше видно, что если бы они вместе объединили свои ноды в один большой кластер и у А была бы свободная CPU, а у Б — свободная память, то понятно, что они сказали бы запустить что-нибудь еще себе. То есть им было бы выгоднее объединиться, чем жить по раздельности. Это соображение — чисто с точки зрения пользователей. На самом деле есть еще разные соображения просто с человеческой точки зрения — что чем больше у вас разных сущностей, тем тяжелее их поддерживать, потому что понятное дело, что за каждым кластером должны быть люди, которые за него ответственны, которые могут что-то починить, если что-то ломается. Поэтому чем у вас меньше таких сущностей, тем меньше вам нужно держать отдельных людей, которые за этим будут следить. Более того, можно эффективнее утилизировать ресурсы. Однако важно понять, как так распределить ресурсы, чтобы было верно следующее.
Что будет подразумеваться под честностью? Что не должно случиться так, что пользователю А выгоднее отделиться, чем не отделяться. Хочется, чтобы стратегия была такой, чтобы всем было выгодно собраться вместе. Стратегия FIFO, очевидно, не является такой, потому что все собрались вместе, встали в очередь А, В и С, но А и В съели весь кластер, С не досталось ничего. Он скажет: «Ребята, так дело не пойдет. Давайте я свои 50 машин заберу, и вы сами запускайтесь. Так у меня будет хотя бы 50 гарантированных машин, а так мне в стратегии FIFO ничего не дали». Напишу английские версии. Честность по-английски в данном контексте называют fairness.
Второе свойство — что ресурсы не должны простаивать. По-английски оно называется страшным способом, а именно pareto efficiency. Это из экономики пришедший термин. Не так важно. Если вам будет интересно почитать, то вы будете понимать, по каким словам все это дело гуглить или яндексить.
Что значит «ресурсы не должны простаивать»? Это тоже естественное требование стратегии. Если к ней пришла нода, у этой ноды есть свободные ресурсы и есть хотя бы одна задача, которую на этой ноде можно запустить, планировщик должен взять ее и не запустить. Он не должен говорить: «Ну, я уже вроде всем по-честному раздал. Хватит, больше ничего не буду делать». Так не пойдет. Если он понимает, что у него есть свободные ресурсы и он на эти них что-то может запустить, то он должен это запустить. Это совершенно естественное требование.
И третье, тоже достаточно важное и неочевидное требование — что невыгодно обманывать. По-английски это называется strategyproofness. Как мы знаем, пользователь приходит и задает то, сколько ресурсов должна съедать одна задача его операции. Не должно быть так, что, допустим, его задача хочет 1 CPU и 4 Гбайт памяти, а он нам взял и сказал — 1 CPU и 5 Гбайт памяти. Если случится так, что он нас обманет, а мы ему за счет этого еще и больше ресурсов дадим, и он сможет больше своих задач запустить, то это будет непорядок, потому что пользователям будет выгодно задать ограничение побольше, чтобы себе побольше получить. Хочется, чтобы пользователям было невыгодно обманывать. Хочется, чтобы они всегда говорили как можно более правдиво о своих потребностях, чтобы, если они говорят неправдиво, им же от этого стало только хуже. Потому что иначе пользователи поделят как-то кластеры, а потом кто-нибудь начнет обманывать кого-нибудь и за счет этого получать бо́льшую долю кластера. Будет нехорошо. Это свойство на словах. А дальше его, понятное дело, для каждой конкретной стратегии можно как-то формализовать. Мы сегодня посмотрим на одну такую формализацию, что она означает. Доказывать, наверное, не будем. Это про свойства.
Теперь давайте я покажу стратегию, которая этим свойствам удовлетворяет. Называться она будет DRF — dominant resource fairness. Эта стратегия будет частной, ресурсы у нее не будут простаивать, то есть она будет pareto efficient и strategyproofness. Однако, к сожалению, в ней будет одно неприятное свойство: каждый конкретный пользователь не может обмануть так, чтобы ему стало лучше, но пользователи могут сговориться и таким хитрым образом обмануть систему, что все-таки кому-то из них станет лучше, и никому не станет хуже. Но про это я приведу пример, мы чуть позже поговорим.

Чтобы рассказать о том, как работает dominant resource fairness, надо ввести немножко понятий и определений. Давайте введем S — это будет вектор ресурсов всего нашего кластера. Некоторый S=(S1,...,Sr). В нашем случае было как раз 3200 CPU и 6400 Гбайт памяти. R тут означает количество ресурсов. Понятное дело, в зависимости от того, что вы можете в своей системе учитывать — в каких-то системах учитывать диск можно, в каких-то нельзя, — количество этих ресурсов бывает разное. Но всегда есть два очевидных — CPU и память.
Кроме того, пусть у нас есть некоторые наши задачи. Операция 1, операция 2 и т. д. Имеются в виду вычисления, которые состоят из каких-то конкретных задач. Кроме того, как мы говорили, люди как-то их распределяют. Пусть это распределение будет задано некоторыми весами: будет вес 1, вес 2 и так далее, вес N. Сумма весов пусть будет равна единице. Весы отнормированы. То есть они как-то решили, какой вес у какой операции должен быть и как они хотят поделить ресурсы и кластеры.
Также нам нужна такая вещь, как вектор требований операции — Dk. У нас был пример. Этот вектор может быть 1000 * (1, 4). 1 — CPU, 4 — память. Я для удобства пишу, можно было записать как (1000, 4000). Когда у нас есть такой вектор, чтобы формально с ним можно было работать и чтобы приземлиться, у нас, понятное дело, должны быть одинаковым способом зафиксированы величины, в которых мы меряем CPU, память и т. д. Допустим, мы их даже одинаково зафиксировали здесь и здесь, а дальше удобно одно на другое поделить, чтобы понять, какую долю ресурсов всего кластера хочет наша конкретная операция.
Представим, что мы посчитали такую вещь, как (Dk1/S1,Dk2/S2,...,Dkr/Sr). Это будет вектор, который состоит из каких-то компонент. Каждая компонента означает, какую долю от всех ресурсов этого кластера хочет данная операция. После этого можно пойти и посмотреть на максимальную компоненту среди всех этих чисел. Возьмем здесь argmax. Тогда эта компонента argmax и будет называться доминантным ресурсом этой операции. Определение — доминантный ресурс операции k.
Пусть у нас здесь останется 3200 и 6400, и пусть у нас D1 = 1000 * 1,4. Тогда этот вектор будет выглядеть следующим образом: 1000/3200, 4000/6400. Видно, что вторая его компонента больше, чем первая, поэтому доминантным ресурсом у этой операции будет являться память. А если мы посмотрим на другую нашу операцию, в которой было 10 CPU и 1 Гбайт памяти, то у нее, напротив, доминантным ресурсом будет являться CPU. То есть доминантный ресурс — это такой ресурс, доля которого в пожеланиях этой операции наибольшая.
Кроме этого, у каждой операции наша доля работает. Что-то запускается, что-то заканчивается, и в каждый момент времени есть такое понятие, как usage — имеется в виду реальное потребление операции. И Uk — это будет потребление ресурсов операцией K. То есть если у нее сейчас запущено сколько-то ее задач, то Uk будет означать, сколько всего ресурсов эти задачи сейчас потребляют. То есть это тоже какой-то вектор, который пропорционален вектору Dk — потому что мы всё запускаем пропорционально вектору Dk. Когда у нас определено потребление ресурсов операцией k, можно ввести понятие uk. Это будет доля потребленных ресурсов.
Хотелось бы сразу говорить о доле. Вся проблема в том, как ее определить. И dominant resource fairness говорит о том, как определить долю ресурсов кластера, которую съела данная операция. Если у нас один ресурс, то определить ее просто: берем количество этого ресурса и делим на суммарный ресурс в кластере. А у нас ресурсов много, и они до конца не понятные. Dominant resource fairness предлагает определить долю потребления ресурсов конкретной операции, то есть одно число, просто как долю максимального ресурса в данной операции. S=(S1,...,Sr). Это число будет называться usage ratio или долей потребленных ресурсов данной операции.
Когда определена такая доля, можно начать говорить о честности в рамках стратегии DRF. Честностью будет называться следующая вещь. Скажем, что стратегия DRF честная, если для любой операции верно, что доля ресурсов, которые она потребила или потребляет при некотором количестве итераций больше либо равна ее весу (Uk ≥ Wk). То есть если операции пообещали 20% ресурсов кластера, значит, по крайней мере, по доминантному ресурсу этой операции ей должны дать 20% этого кластера. Если самих ресурсов она вообще не хотела или хотела существенно меньше — ей дадут их меньше. Это не до конца очевидно. Но в некотором смысле понятно, почему, если стратегия DRF честная, она будет честной и в нашем общем случае, почему никому не будет выгодно отделиться.
Представьте, что кому-то обещали 20%, ему 20% таким способом дают, а он взял и решил: «Нет, невыгодно. Я лучше отделюсь». Тогда у него, в частности, и по доминантному ресурсу после отделения будет иметься в его маленьком кластере 20%. Это означает, что больше, чем здесь, он запустить все равно не мог, потому что у него ресурсы ограничены. И все плохо, он уперся. А за счет того, что он с кем-то объединился, можно сделать так: когда другой хочет, наоборот, CPU, а не память, они вдвоем съедят больше ресурсов в кластере и получат долю больше, чем обещанная им Wk.
Мы объяснили, что значит честное DRF. Теперь, когда мы объяснили, что это такое, хочется понять, есть ли такие стратегии, и если есть, то как должен быть устроен алгоритм, который такого достигает. Он будет выглядеть следующим образом.
Прежде чем рассказывать, как он устроен, давайте поймем, почему он есть. На самом деле, понятно, почему он есть — потому что, как мы только что рассуждали, если кто-то отделился со своими 20% кластера, то он, когда всё займет, получит в точности вес Wk в этом кластере. Если мы смотрим на ресурсы кластера как на два больших столбика CPU и RAM, то, допустим, тут пообещали кому-то 50%, кому-то 20%, кому-то 30%. Допустим, они как-то тут съели свои ресурсы: этот съел все это и немножко RAM, а этот съел сколько-то CPU и весь RAM. Это операция 1, это операция 2, а это операция 3. И третья съела весь RAM, но не всё CPU. Если наша стратегия даже вот так распределит, то уже будет все хорошо — уже будет Uk ≥ Wk. Но заметим, что у нас еще остались ресурсы: у нас остались еще CPU, недораспределенные от второй и третьей операций. И еще остался нераспределенный RAM. Стратегия может как-то их распределить. Как именно она это сделает, мы сейчас увидим, когда будем описывать алгоритм.
Если мы просто поделили ресурсы пропорционально, то распределить так, чтобы каждый распоряжался своим ресурсом, — понятное дело, получится. Худший случай для нас — когда они все хотят одного ресурса. Тогда они все в него упрутся, все остальные будут недоиспользованы, и им будет все равно. Получится эквивалент того, как если бы они разделились на отдельные кластеры, или того, как если бы они не делились. Но они будут использовать разные ресурсы, им нужно получить выгоду.
Как будет устроена стратегия? Есть у нас операции: операция 1, 2, 3 и т. д. Есть наш планировщик. Ему надо как-то понять. Сейчас есть какое-то текущее положение. Мы знаем веса этих операций — W1, W2, W3 — и знаем их реальное текущее потребление. В нашей стратегии теперь надо как можно быстрее понять. К ней пришла нода, сказала: «У меня есть свободные ресурсы. Кого мне запустить?» Нам надо как можно быстрее понять, кого запустить.
Будем делать следующим способом. Наша стратегия будет просто итерироваться, перебирать все наши операции, и каждый раз выбирать ту, у которой как можно меньше значение S=(S1,...,Sr). Выбираем такое k, что выражение Uk/Wk минимально. Как эффективнее это сделать — уже алгоритмический вопрос. Можно какую-нибудь очередь с приоритетами завести у себя в памяти и в этой очереди с приоритетами просто хранить указанные значения. И когда у нас что-то завершается, мы Uk будем уменьшать, а когда что-то увеличивается — увеличивать. Что будет делать стратегия? Она каждый раз будет брать операцию, в которой это значение минимально, и говорить: «Ой, я одну задачу для нее сейчас собираюсь запустить». Увеличивается Uk на сколько-то. И повторять до тех пор, пока свободные ресурсы на ноде, которая к ней пришла, не закончатся. Так она поймет, какой набор задач ей надо на этой ноде запустить, пойдет и запустит их. И обновит значение k.
У нас верно следующее: если мы начнем все распределять с нуля, то получится Uk ≥ Wk. Так как мы это знаем, то понятно, что если забыть про вопрос погрешности, эта стратегия как раз найдет такое решение, у которого все Uk будут больше или равны Wk — потому что она каждый раз дает минимальное значение и по чуть-чуть их увеличивает. Из-за гранулярности такое может не случиться. Мы видели пример, когда есть у нас 10 CPU — а это очень большая доля на каждой вычислительной ноде — и может быть так, что мы первую раздали, а дальше уже указанные 10 CPU никому дать не можем. Это отдельный вопрос, про который мы скоро поговорим.
Рассматривая этот вопрос в теории, для простоты считают, что все наши операции бесконечно гранулярны. То есть если у нас имеются наши векторы ресурсов Dk в операции, то можно считать, что наша задача — это ε*Dk, где ε произвольно маленькое. В теории всегда считают, что если у нас есть какая-то операция и у нее есть какой-то запрос ресурсов, то мы можем задать сколь угодно малую величину, пропорциональную этому запросу ресурсов, и просто запустить ее как идеальную задача. Понятное дело, что в жизни это не так, но для теории удобно так рассуждать.
Мы поняли, как устроена стратегия, поняли, что она является честной и в своем смысле, и в смысле общего определения честности. Почему она не допускает выгоды от единичного обмана? Давайте мы оставим это вам как упражнение. Это совсем несложно доказывается. Можно доказать, что если кто-то обманул, то от этого ему станет только хуже. Можно даже какие-нибудь рассуждения на пальцах провести. Например, если операция обманула по тому ресурсу, который у нее доминантный, то затем это число у нее начнет увеличиваться быстрее, чем раньше. То есть ей вроде бы дали такой же кусочек, а оно у нее увеличилось сильнее. За счет того, что оно у нее увеличилось сильнее, ей по факту дадут меньше этого ресурса. Поэтому если операция запросила 1000 CPU вместо одного, который ей реально нужен, то ей дадут совсем мало CPU.
Давайте нарисуем какие-нибудь примеры. Когда мы будем рисовать примеры, можно немножко упрощенно смотреть на картину. Можно считать, что у наших операций бесконечно большой demand, то есть запрос ресурсов. И еще одно допущение, о котором я говорил, — что они хотят ресурсы в процентах от ε.
Представьте, что у нас есть две операции. Когда мы говорим, что у них бесконечно большой demand, дальше бессмысленно говорить о каких-то конкретных величинах. Бессмысленно говорить, что у них 1000 CPU или 2000 Гбайт памяти. Нас, на самом деле, будет интересовать только пропорция, в которой каждая операция хочет своих ресурсов. Давайте считать, что пропорция, в которой первая операция хочет своих ресурсов, — это (1, ½), а вторая, например, хочет в пропорции (½, 1). А раздавать мы будем так: мы тоже все ресурсы, которые у нас имеются, отнормируем, и станем считать, что на нашем кластере единичный вектор наших ресурсов, например, такой — S=(S1,...,Sr). Вопрос: как наша стратегия поступит в этом случае? Какую долю кластера она даст в первой операции, какую во второй? Можно ли это понять из описания стратегии? Понимает ли кто-нибудь, какие здесь будут вектора и какую долю кластеры дадут первой операции, а какую второй?
Смотрите, как все будет происходить. Посмотрим на небольшой промежуток времени, когда мы что-то выдаем первой, а что-то выдаем второй, причем мы всегда выдаем той, которая минимальна. Поэтому можно считать, что когда у нас прошло немного времени, то мы дали чуть-чуть, и чуть-чуть мы дали одинаково пропорционально что первой операции, что второй. Причем мы даем пропорционально их доминантному ресурсу. Через небольшой промежуток времени у нас получится следующая картина. Здесь будет (ε, ε/2), здесь — (ε/2, ε), а ресурсов, которые у нас останутся незадействованными, свободными, будет столько: (1 – 3ε/2, 1 – 3ε/2). Дальше эта ε будет увеличиваться, и до каких пор? В какой момент мы перестанем что-либо раздавать? Какой будет ситуация в конце? Мне кажется, надо решить простое уравнение. У нас все закончится в тот момент, когда количество ресурсов здесь станет нулевым, необязательно по всем векторам, но в данном случае — по всем, поскольку мы сможем пропорционально всем раздать. Все закончится тогда, когда в корне станет ноль. Если мы раздаем пропорционально, то здесь получится (⅔, ⅓), а здесь, наоборот, (⅓, ⅔).
Весь первый и весь второй ресурс мы раздали, причем раздали пропорционально. Сразу напомню, что вес W у нас здесь был 0,5, а реальная доля U, которую мы дали, будет равна ⅔. У этой операции точно так же. Это тот случай, когда им было выгодно объединиться.
Бывает так, что неважно, объединились они или нет. Давайте нарисуем еще какой-нибудь пример. Пусть здесь, например, (0,1), а здесь (1,1). Как распределятся ресурсы после того, как DRF закончит свою работу и все их раздаст? Какой вектор ресурсов будет дан первой операции, какой вектор ресурсов будет дан второй операции? Может быть, какие-нибудь предположения или идеи? У первой операции доминантным является что первый, что второй ресурс, у второй — только второй ресурс. Поэтому можно считать, что доминантный у обеих операций второй ресурс, и поэтому оно будет раздавать пропорционально второму ресурсу.
Пополам, да. То есть будет (½, ½), (0, ½).
— А как мы определяем, какое решение с двумя будет?
— В нашей задаче изначально был какой-то вектор реальных ресурсов на кластере, и здесь тоже были какие-то реальные вектора потребления. А тут мы уже отнормировали, и то, что здесь написано, — это после нормировки. Причем мы это все отнормировали до единицы, и как бы максимальный ресурс у нас был равен единице. То есть все эти вектора уже в упрощенной форме выглядят как одна компонента. У них обязательно один этот доминантный ресурс, а все остальные — от 0 до 1. Они тоже могут быть равны одному, но больше одного быть не могут. То есть такой вектор обозначает, в какой пропорции относительно всех доступных на кластере ресурсов находится требование в этой операции. Эта операция пропорционально хочет первого и второго ресурса. А эта операция первого ресурса не хочет вообще, а хочет только второй.
Давайте я приведу пример, как сговор помогает выиграть, помогает получить себе дополнительный ресурс. Пример достаточно хитрый, но не то чтобы суперсложный. И это тоже хороший повод потренироваться на том, как DRF работает.
У нас будет четыре операции и три ресурса. Первая операция будет хотеть только CPU. Вторая операция тоже будет хотеть только CPU, то есть только первый ресурс. Третья операция будет хотеть только память, а четвертая операция будет чуть более хитрая — она будет хотеть и память, и еще третий ресурс, давайте называть его сетью. Есть у нас такая картина. Я здесь не рисую веса. Когда я не рисую веса, это означает, что раздать мы хотим пропорционально. Тут можно было бы рисовать веса, то есть по факту веса везде ¼. Но когда они все одинаковы и равны ¼, я просто их опускаю, потому что подразумевается, что это и так понятно. Когда веса не будут пропорционально разделены, мы будем явно выписывать, сколько какого веса на каком ребре написано, то есть в какой пропорциональности они раздаются.
Давайте поймем, как в этом случае отработает DRF. Вот он пропорционально всем раздает. Чтобы понять, как он работает, полезно представить себе следующее. Всегда есть какой-то ресурс, у которого суммарные требования здесь больше всего. У какого ресурса суммарные требования здесь больше всего?
— У первого CPU.
— Да, потому что у него суммарные требования — 2, у памяти суммарные требования 1,5, а у сети вообще 1. Поэтому, когда мы будем раздавать пропорционально, первым закончится этот ресурс. Это означает, что можно дойти до ситуации (½, 0, 0), (½, 0, 0). Этим мы тоже должны были дать долю ½, поэтому здесь будет (0, ½, 0), а здесь — (0, ¼, ½). У нее доминантный ресурс третий, и мы ей столько выдали. После этого у нас первый ресурс закончился, и больше мы ничего ни первой, ни второй операции не даем. Теперь мы даем только третьей и четвертой операции, и тоже даем столько, чтобы у них все росло пропорционально.
— Почему мы четвертой даем сеть ½?
— А мы хотим, чтобы у всех была ½ с точки зрения их доли потребленных ресурсов.
— А остальным же не надо.
— Нет, мы еще не дораздали, мы смотрим. Как работает алгоритм — он всем пропорционально раздает, повышает долю. Потом какой-то ресурс мог закончиться. Мы дошли до того момента, когда первый ресурс закончился. Теперь он уже понимает, что этим давать не надо ничего, потому что ресурса просто нет, и он начинает пропорционально давать этим. Когда он будет пропорционально раздавать второму и третьему, чем это все завершится?
— Ресурс закончится.
— Да. Какой ресурс закончится?
— Второй.
— Да. Причем у них должна быть пропорциональная доля. Тут можно было бы решить линейные уравнения, но кажется, что все и так понятно. Все закончится, когда здесь станет (0, ⅔, 0), а здесь — (0, ⅓, ⅔). То есть у нас теперь ресурсом, в который мы упремся, будет память, потому что память — второй по надобности ресурс в нашем кластере среди оставшихся незаблокированных операций. Раз мы в него упремся, значит, нам надо понять, в какой момент мы на нем остановимся. Дальше у нас есть у этого доминантный ресурс — сеть, у этого память, и надо понять, что сеть в два раза больше, чем память. Они в пропорции ½ по памяти и остановятся. То есть конечная картина такая: этому дали (½, 0, 0), этому (½, 0, 0), этому (0, ⅔, 0), этому — (0, ⅓, ⅔).
Для понимания давайте выпишем здесь веса. Здесь вес был ¼, а usage ½. То есть мы дали в два раза больше, чем он мог рассчитывать. Здесь тоже ¼, ½. Веса у них у всех ¼, а дали ему ⅔, то есть даже еще больше. И тут точно так же — вес ¼, а дали ⅔. Оказывается, что теперь некоторые участники этой системы могут сговориться и за счет этого выиграть себе побольше ресурсов. Что значит сговор группой? Это означает, что несколько участников системы могут сговориться, собрать свои ресурсы, и в итоге получится так, что каждый из них получит долю не меньше, чем у них была до этого, а кто-то еще и строго больше. То есть понятное дело, что иногда можно врать, и ничего от этого не получать, не проигрывать. Такое возможно, потому что есть какой-нибудь четвертый ресурс, который никто не использует на кластере, вы про него соврали, вы его получили, но он все равно не нужен — доля у вас какая была, такая и осталась. Здесь же все хитрее. Можно наврать следующим образом.
Сговариваться у нас будут первые трое. Первый и второй просто возьмут и соврут про сеть, которая им не нужна. Окажется, что если они соврут про сеть, то третий, который требует только память, неожиданно получит больше ресурсов, чем было бы, если бы они не соврали. Будет (0, ½, 1). Здесь таких ресурсов, которые требуют максимум, целых два. Тут и по первому ресурсу сумма 2, и по третьему ресурсу сумма 2. Поэтому мы остановимся тогда, когда остановятся одновременно оба этих ресурса. Это будет в тот момент, когда мы раздадим ½, то есть придем к такой ситуации: будет (½, 0, ¼), (½, 0, ¼), (0, ½, 0), (0, ¼, ½).
Наша стратегия DRF всем дала по ½ — казалось бы, все честно и справедливо. Причем первый и третий ресурс у нас уже закончились. Поэтому остался только второй ресурс — память, и понятное дело, кому его надо отдать. Его осталась ¼, значит, надо его этому и отдать. В итоге он получит (0, ¾, 0), что, очевидно, больше, чем (0, ⅔, 0). Таким образом, получилась хитрая вещь: первые двое наврали про сеть, третий выиграл по памяти, хотя сеть никому из них троих вообще не была нужна. Такая проблема есть, и как ее решать — непонятно. Историческая справка такая: сначала утверждалось, что это свойство — оно из следующей статьи про алгоритм DRF — верно, и было доказательство на пальцах. Мы просто тоже занимались этим вопросом, придумали свою стратегию для более сложного случая, и тоже попытались доказать для нее свойства. Пока мы пытались доказать для нее свойства, мы нашли контрпример для нашей стратегии. Потом поняли, что раз мы нашли контрпример для нашей стратегии, то давайте попробуем его же и для исходной. И выяснилось, что и для исходной стратегии это неверно. Исходная стратегия не обладает этим свойством. Дальше мы попробовали найти стратегию, которая является одновременно и честной, и такой, что ресурсы не простаивают, и не допускающей сговора. Непонятно, существует ли такая стратегия. Все простые разумные стратегии — для них для всех находится какой-нибудь неприятный контрпример, который нарушает третье свойство. Есть такая или нет — не до конца понятно. Казалось бы, задача достаточно простая, комбинаторная — просто какие-то вектора, как-то распределяются ресурсы, требования достаточно просто описываются. А есть стратегия или нет — не до конца понятно. И как найти такую стратегию или как доказать, что ее нет, — тоже не до конца понятно. Если вам это интересно, то можете на досуге подумать и что-то придумать в этом месте.
А я пока расскажу про две вещи, которые не упомянуты. Одна вещь состоит в том, что это все замечательно, но на практике описанная стратегия DRF тоже работать не будет по одной простой причине, в целом схожей с тем, что у нас происходило в стратегии FIFO. Представьте, что у вас есть три пользователя: A, B и C. Вы пообещали этому 20%, этому 30%, этому 50%. Дальше есть у вас кластер, ночь, все простаивает, никто ничего не запускает. Наступает утро, приходит пользователь А и запускает огромную свою операцию. Понятное дело, что пока B и C ничего не запустили, мы должны все ресурсы кластера отдать первому пользователю, потому что он запустил операцию, и чего мы будем его сейчас как-то ограничивать? Мы отдадим ему все ресурсы, а после этого к нам придут B и C со своими запросами. Они придут, поставят операции, и ничего не произойдет. А первая операция бежит и не собирается заканчиваться. То есть как только задачи первой операции начнут заканчиваться, то освободившиеся ресурсы будут даваться В и С, но если у первой задачи все не заканчивается и не заканчивается, то В и С не будет ничего доставаться, они будут недовольны, будут писать вам, звонить, придут к вам ногами, начнут жаловаться — произойдут разные неприятности. Чтобы такого не было, нужно, чтобы в вашей системе была некоторая стратегия вытеснения. Стратегия вытеснения — это некоторый план, что если кому-то плохо, то как бы кого-нибудь, кому очень хорошо, немножко вытеснить с кластера, сказать: «Что-то у вас много бежит задач. Давайте мы какие-нибудь прекратим».
К сожалению, на эту тему достаточно мало теории. Мы немножко ее выработали, и тоже написали про это статью. Но идея в целом простая. На практике работает следующая идея. Если у вас есть какие-нибудь операции, обещанная этим операциям доля ресурсов меньше, чем то, сколько им дали. Тогда такую операцию называют страдающей, и говорят, что надо ради нее что-нибудь вытеснить. Но сразу вытеснять — наверное, плохая идея. Можно немножко подождать — вдруг что-нибудь само закончится. Но если оно какое-то время не заканчивается, то тогда просто начинают вытеснять, причем вытесняют тех, у которых больше всего доля, а кроме того, тех, у кого самые короткие задачи. Было бы обидно, если кто-то запустил свои операции, они уже час отработали на кластере, уже почти закончились, все сделали, а мы сейчас пойдем и прекратим их. Поэтому понятное дело, что надо вытеснять тех, у кого задача, например, запустилась минуту назад. Она за минуту еще не успела там все сделать, и, наверное, ее можно «убить».
На практике так и делают, а в теории как раз надо вытеснять тех, у кого больше всего доля — чтобы после того, как вы кого-то повытесняли, у вас все сошлось к честной схеме. Теория здесь немножко посложнее, и у нас нет времени еще про нее поговорить.
Еще одна вещь, про которую я не успел поговорить, но кратко скажу — это то, что называется иерархическим DRF или HDRF. К сожалению, пользователям такого не хватает. «20% кластера? Нет, это нам не очень подходит. У нас есть еще важные задачи, неважные задачи, еще что-то». Люди хотят, чтобы у них была не плоская, а сложная иерархия. Хотят, чтобы этому — где ничего внутри нет — ему дали 30%. 30%, но у него внутри есть какие-то свои предпочтения — есть research-задачи, а есть production-задачи. И он хочет, чтобы research из того, что ему дали в кластере, досталось 20%, а production — 80%. Здесь, допустим, тоже два типа задач, и он хочет, чтобы им досталось по 50%. Дальше есть этот, и у него тоже какое-то распределение — 30% и 70%. То есть люди хотят, чтобы система была не плоской, а иерархической, и чтобы scheduler — наш планировщик — это как-то учитывал, чтобы он понимал, что есть такая иерархия, и стремился каждому дать пропорционально тому, сколько ему обещано. Здесь у нас есть какой-то пул, которому мы пообещали 30%, а в нем есть подпул, которому мы пообещали 20%. Это означает, что всем задачам, которые бегут в этом поддереве, должно достаться хотя бы 30%, а среди них задачам из этого подпула должно достаться 30% * 20%, то есть 6%. Он хочет, чтобы этому досталось как минимум 6% от ресурсов всего кластера. Есть такие более сложные требования.

Как бы такое сделать? Есть наивное предложение: «А давайте сложную иерархию превратим в простую иерархию». Мы можем посчитать про каждую вершинку, сколько от доли всего кластера ей должно достаться. Мы посчитали для этой, получилось 6%, а можем для всех остальных посчитать. То есть тут будет 6%, 20%, 15%, 35%, 12% и 12%. И есть идея: давайте просто из этой иерархии сделаем плоскую, в которой будут 6%, 20%, 15%, 35%, 12%, 12%. К сожалению, такая идея не работает. И не работает она следующим способом. Да, этим дадут столько, сколько им пообещали, но после этого может оказаться, что всему этому не дадут его обещанные 30%. А мы договорились, что этому отделу в Яндексе должны давать на кластере 30%. Мы этим всем выдали, а суммарно 30% не набралось, потому что у этих могут быть разные доминантные ресурсы. Может быть, эта хочет память, эта хочет CPU, эта — сеть. Мы суммарно раздали, и даже если все ресурсы, которые они съели, сложить, то как вектор они не будут съедать 30% кластера. Такая вот проблема. Поэтому приходится поддерживать деревья.
Какое второе наивное решение здесь может быть? Давайте наш алгоритм DRF преобразуем следующим образом. Как он раньше действовал? Он находился в корне, смотрел на веса своих детей, смотрел на их потребление доминантного ресурса и тому, у кого это потребление доминантного ресурса, деленное на вес, минимально, шел и предлагал, давал задачу. Мы продолжим делать точно так же. Просто когда мы пойдем сюда, то дальше повторим уже на этом поддереве ту же самую операцию. То есть мы сначала поняли, что этому поддереву дают меньше всего, а потом в этом поддереве пытаемся понять, кому там снова дают меньше всего. Точно так же, выбирая на каждом уровне в каждом узле минимум среди детей, среди отношений их usage к весу, мы будем идти в минимального до тех пор, пока не дойдем до какого-нибудь листа. И уже в том листе, той операции, которая там лежит, предложим задачу.
К сожалению, так тоже не работает. Покажу пример, почему не работает такая стратегия, которая называется naïve HDRF. Не работает она по следующей причине. Давайте посмотрим на такую несложную иерархию. У нас здесь требования только по первому ресурсу, здесь тоже только по первому, а здесь по второму. Что будет, если мы сюда применим нашу naïve HDRF? Будет в целом все хорошо. Сначала мы, наверное, придем к тому моменту, когда мы сюда дали половину, и сюда дали половину. То есть тут у нас стала (½, 0), тут суммарный demand (1, 1), поэтому тут стало (½, ½), которая распределяется как (½, 0), (0, ½). После этого у нас остался еще второй ресурс, и дальше после некоторых итераций здесь станет (0, 1). Казалось бы, все хорошо. Этому дали половину CPU и всю память, а этому — другую половину CPU. Вроде обещания для всех сдержали. Но возникает такая проблема. Допустим, мы пришли к такой ситуации, когда случается проблема: эта операция берет и начинает заканчиваться, у нее заканчиваются ее задачи. Она потихоньку убывает, и становится 0. Что делает scheduler? Он смотрит в корне: «Этому я дал половину всего CPU, память он не просил. А этому я дал всю память, но никакого CPU. Доминантный ресурс у этого — память, у этого — CPU. Раз у этого доминантный ресурс CPU и его ½, а у этого память и она 1, то надо давать тому, у кого поменьше, то есть этому. Scheduler просто пойдет и начнет давать этому еще CPU. И в итоге мы придем к ситуации, когда здесь у нас (1, 0), здесь (0, 0), а здесь (0, 1). И как бы мы это поддерево, этот пул ни обманули, но конкретно эту операцию — обманули. Ей вообще ничего не досталось, у нее все закончилось, и ей ничего больше не дают. Проблема.
Min satisfaction HDRF — один из способов решения этой проблемы. Скажу на словах. Он состоит в следующем: давайте, когда мы будем выбирать, кому давать, то будем смотреть не только на этот вектор и доминантный ресурс всего пула, а для каждого узла в поддереве посчитаем отношение. Обычно, когда у нас дерево, эти узлы, вершинки в дереве, обозначаются какими-нибудь буквами, и пишут usage S=(S1,...,Sr). Оказывается, что если выбирать минимальные из всех таких отношений, то тогда все будет хорошо. То есть мы будем смотреть на отношение и в этом узле, и в обоих его детях. А если у тех есть еще дети, то и в них тоже. Если наш алгоритм будет действовать таким образом, то тогда он всем даст как минимум обещанную там долю.
На этом мы подходим к концу.
Заключение. Как мне кажется, то, что я сегодня рассказал, — хороший пример того, как в идеальной практической задаче, которая встает в моей вполне конкретной реальной работе, возникает некая математическая формализация и математическая задача. Это нечастый случай, и то, что он случился, — это, по-моему, очень здорово. Потому что чаще всего математика и практика немножко по отдельности живут, и изредка что-то из математики находит применение в практике. А когда удается формализовать практическую задачу, привести ее к математической — это очень здорово, и это дает свои плоды, потому что когда ты делаешь что-то наобум на практике, зачастую это не работает — ты получаешь решение наобум. А если ты можешь строго доказать что-то о решении, то это очень хорошо. Это значит, что раз ты смог это строго доказать, то, наверное, оно почти всегда будет хорошо работать. В результате min satisfaction HDRF — это то, что мы на работе придумали, и он обеспечил на 5-10% более эффективный алгоритм. Пользователи перестали страдать, перестали жаловаться, мы стали эффективнее использовать ресурсы кластера, и все стало хорошо. Кроме того, мы нашли ряд ошибок в чужих статьях, поставили некоторые новые вопросы, что тоже здорово. Это интересно взять и поисследовать. К сожалению, времени не очень хватает. Может быть, у кого-нибудь из вас или у кого-нибудь из онлайн-слушателей на это время найдется, и они решат наши открытые вопросы.
Всё. Всем спасибо. Рад был здесь выступать.
Автор: Яндекс






