Декодирование BPSK Модуляции из Звука (или передача данных по воздуху)

Пролог

В сообществе уже был текст про то как звуком передавать данные. Однако там была FSK.

Можно вообще взять микросхему DTMF декодера MT8870 и принимать по 4 бита за раз полностью аппаратно.

В этом же тексте я попробовал исследовать возможность передачи бинарных данных звуком через BPSK модуляцию (она же ФМн-2, она же QAM-2). Почему именно BPSK? Дело в том что эта модуляция очень распространена и обладает хорошим шумоподавлением. Потом BPSK модуляция прямо сейчас буквально пронизывает наши тела, каждый день, так как BPSK сигнал - это физический интерфейс, который испускают GPS спутники. Также BPSK якобы используется в WiFi и Sigfox. В общем есть причины, чтобы понять как это работает.

BPSK модуляция это способ передавать бинарные данные на высоких частотах. Пришла эта тема из радиоэлектроники. Радо возможно передавать только на высоких частотах. В радио чем выше частота несущей, тем меньше нужна антенна. Однако ничто не запрещает использовать BPSK модуляцию и в волнах другой природы. Например в звуке, оптике или вовсе в коаксиальном кабеле. Со стороны ЦОС и SDR обработки, что радио, что звук, что интенсивность света, что напряжение - всё не имеет никакого значения. В RAM памяти есть массив знаковых семплов и надо его обработать.

Зато записывать и воспроизводить звук намного дешевле, проще и удобнее, чем радиоволны. Вы где-нибудь видели диктофоны для радиоволн? А звуковые диктофоны присутствуют в любом мобильном телефоне + проигрыватель аудио файлов. В том числе и самых простых - *.wav файлов.

Постановка задачи

Декодировать BPSK из записи звука на диктофоне.

Теория

Все эти модуляции (ASK, OOK, BPSK, FSK, 256-QAM, CSS, GFSK, MSK) можно отнести к интерфейсам физического уровня модели OSI-7, так как модуляции поясняют как именно передаются биты в физической среде. BPSK тоже можно рассматривать как интерфейс физического уровня.

Какие есть параметры у BPSK сигнала?

Вот так выглядит BPSK сигнал в частотной области. Br - это битовая скорость.

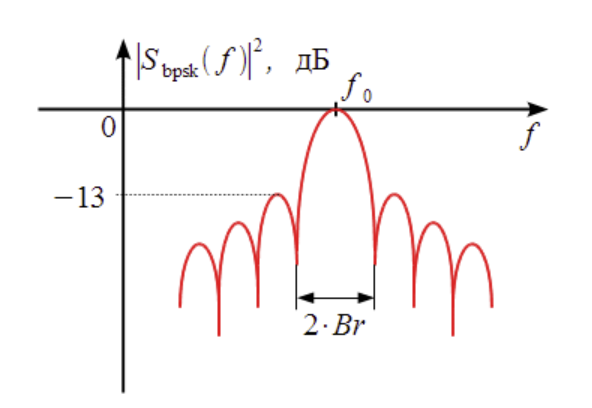
При понижении Br битовой скорости BPSK вырождается в синус. Поэтому при уменьшении битовой скорости ширина сигнала сужается. При повышении битовой скорости BPSK спектр расширяется.

chip (чип) - это минимальный фрагмент BPSK сигнала, где фаза несущей частоты не меняется. Фактический в BPSK чип это один бит данных.

Что надо из софта?

Реализация

Модуляция BPSK (Encode)

Прежде всего я синтезировал *.wav файл который содержит бинарные данные 0x55aa которые закодированы BPSK модуляцией. Почему именно wav? Да потому что это самый простой формат аудиофайлов. Это просто массив int(ов) упакованный в бинарный файл с прикрепленной спереди преамбулой (заголовком). Заголовок содержит все необходимые метаданные про этот звуковой трек: частота дискретизации, размер семпла, количество каналов.

Вот он перед вами. Как можно заметить это самая настоящая BPSK модуляция.

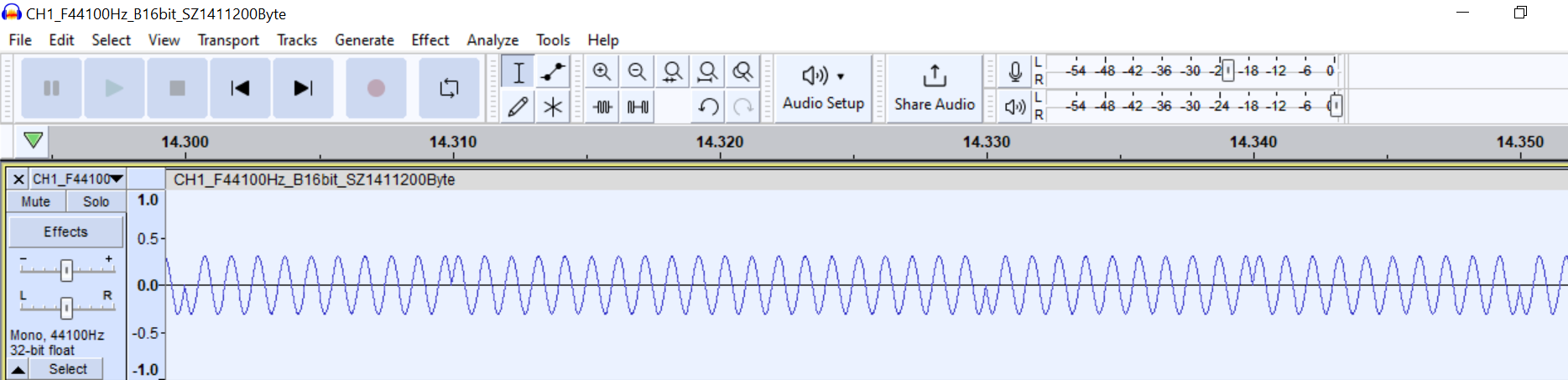
На слух звучит такой сигнал как работающий насос для колодца.

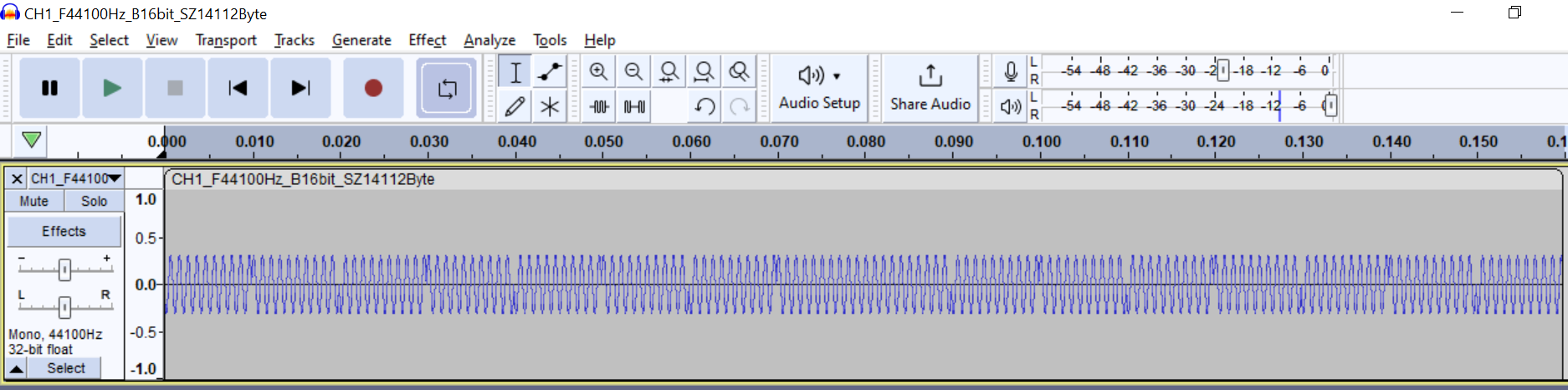
Я закинул *.wav файл через мессенджер себе на смартфон и стал воспроизводить *.wav обыкновенным музыкальным проигрывателем из-под Android смартфона.

Демодуляция BPSK сигнала (Decode)

В технических системах принять, что бы то ни было всегда много сложнее, чем что-то отправить. Кинуть мяч проще, чем его поймать. UART приёмник намного сложнее UART передатчика. Так и тут в модуляциях приёмники намного сложнее передатчиков. Тем не менее надо декодировать принятый BPSK сигнал.

Прежде чем кидаться декодировать BPSK семплы надо подсказать декодеру на какой несущей частоте мы будем искать сигнал и какая битовая скорость в данном потоке. В случае с SDR также указать частоту дискретизации ADC.

Каков план?

Классической электрической цепью для демодуляции BPSK сигнал является Costas Loop. Вот он перед вами.

Costas Loop - это система автоматического регулирования (привет ТАУ). Её задача управлять фазой гетеродина, чтобы она непрерывно соответствовала фазе входного сигнала. Особенность гетеродина Costas Loop в том, что тут можно регулировать фазу несущей частоты. У фазы тут главная роль.

Достоинство Costas Loop в том, что он саморегулируемый. Передатчик можно даже двигать, а схема Costas Loop сама подстроится под новую фазу приходящего сигнала. Каждый новый семпл подстраивает фазу гетеродина. Теоретически Costas Loop можно собрать даже из аналоговых компонентов.

Тем не менее, эта цепь с непривычки может показаться сложной. Далее небольшой комментарий по схеме.

Фаза 1: Перемножение

На первой стадии поступающий BPSK сигнал на несущей 1kHz разделяется на две копии и каждая перемножается на косинус и на синус версию сигнала с гетеродина. Частота гетеродина тоже 1kHz как и частота несущей. Это работа квадратурного смесителя.

Фаза 2 Удаление высокочастотной составляющей

Как известно из школьной тригонометрии перемножение синуса на косинус дает высокочастотное слагаемое. Его надо отбросить. У меня в SDR реализации это производится цифровым FIR фильтром 200го порядка. В качестве частоты среза я выбрал удвоенную битовую скорость BPSK. В данном случае это 200 Hz

Фаза 3: Выделать фазовую ошибку (фазовый дискриминатор).

Измерить фазу ошибки между входным сигналом и гетеродином можно аж тремя способами.

a) Измерение фазы арксинусом

Благодаря тому, что мы смешиваем сразу с двумя версиями гетеродина, мы получаем фазовую ошибку сигнала по отношению к гетеродину. Ошибка получается численно. Понятно, что надо сконфигурировать этой фазовой ошибкой сигнал самого гетеродина. При этом можно заметить, что в Costas Loop(е) чистые данные снимаются с real плеча I. А это значит, что там внутри синус всегда должен обращаться в единицу. Синус обращается в 1 только при 90 градусах (при pi/2). Поэтому после обработки каждого семпла надо в фазу гетеродина присвоить новую фазу: фаза ошибки + pi/2. При этом фаза ошибки считается аналитический формулой с арксинусом.

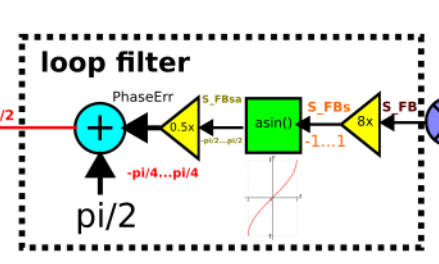
Однако минус этого способа в том, что входной сигнал должен быть нормализованным. То есть его амплитуда всегда была 1. Однако на практике такого никогда не бывает. Из микрофона сигналы приходят с шумами. Поэтому такой способ я не буду использовать.

b) Измерение фазы арктангенсом

Ошибку можно измерять функцией atan2(). Причем ошибку по фазе надо интегрировать перед тем как присвоить гетеродину. Так интерактивно и получится горизонтальное сигнальное созвездие. Такой регулятор будет прижимать вектор (I,Q) в ближайшую сторону чтобы получить горизонтальное созвездие.

b) Измерение фазы углом между векторами

Ошибку по фазе можно определить при помощи линейной алгебры. По сути надо найти угол между вектором, который лежит на оси x (1, 0, 0 ) и вектором, который образуется на выходе квадратурного смесителя (I, Q , 0).

Из-за шума ошибка по фазе может изменяться с очень высокой частотой. Даже если источник изначально статический. Поэтому ошибку фазы следует пропустить через ещё один фильтр нижних частот (FIR или IIR). Также надо управлять фазой гетеродина через PID регулятор. Пропорциональный коэффициент обычно получается на 2 порядка меньше 1. Интегральный коэффициент можно сделать около единицы.

Фаза 4: Компаратор

После фильтра на проводе I данные всё еще аналоговые. Наша же цель снять бинарные данные. Для этого надо пропустить сигнал с провода I_Filt через компаратор. А лучше даже для подстраховки пропустить через триггер Шмитта. Это будет ещё один своеобразный фильтр.

Фаза 5: Выделить биты данных

Однако выход компаратора это всего лишь четкая картинка. Для софта верхнего надо выделить именно биты с данными. Сейчас ситуация такова, что на один бит приходится 441 семплов ADC сигнала.

Поэтому надо выполнить так называемую децимацию (Downsampling). Из N семплов оставить один. Такая задача идеально решается конечным автоматом. Вот граф конечного автомата прореживания.

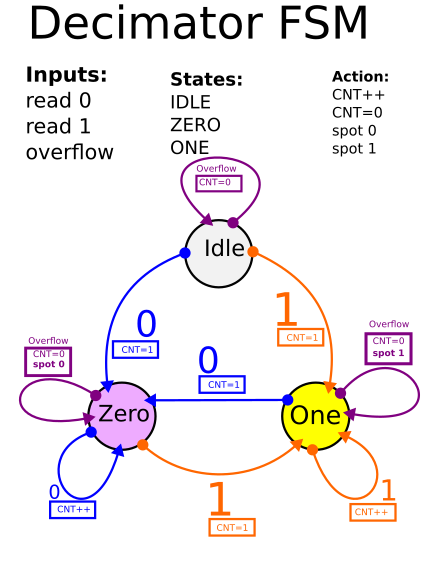
Как только счетчик принятых единиц (или нулей) досчитает до определенного количества семплов samples_per_bit, конечный автомат прореживания выдаст сигнал, что распознан бит (1 или 0).

Фаза 6: Выделение байтов

На выходе демодулятора BPSK мы получаем только поток битов, которые изначально были наложены на несущую частоту.

Каким образом можно снять сами данные и сформировать из них байты? Поиск начала байта - это уже задача какого-то протокола канального уровня. Как вариант можно вводить что-то похожее на преамбулу начала пакета и парсить её из бинарного потока. Но это уже не касается BPSK.

Отладка

Любая разработка начинается только тогда, когда появляются средства отладки. Отлаживать BPSK декодер (как и любую другую модуляцию) принято при помощи графиков сигнальных созвездий. В идеале диаграмма BPSK должна быть в виде двух кластеров (скоплений) на оси X [она же ось I, она же действительная часть, она же выход cos()*signal()] равноудалённых от начала координат.

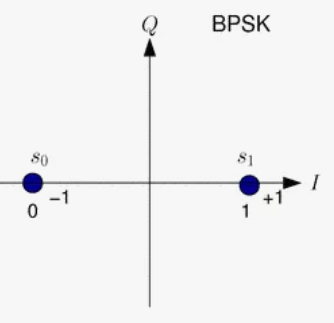
Вот пример одного реального сигнального созвездия. Как по мне это весьма причудливо выглядит.

Отладка на рафинированном файле

Прежде чем кидаться декодировать аудио файл с диктофона надо сперва подать на BPSK декодер просто чистый рафинированный массив семплов BPSK сигнала без какого бы то ни было шума. Надо убедиться, что мой SDR алгоритм написанный на чистом Си вообще работает в этих тепличных условиях.

При разных настройках порядка FIR фильтра сигнальное созвездие может принимать причудливые формы.

Даже если нормализовать входной сигнал пропустив через функцию sign, то всё равно выделяются биты с данными

Это сигнальное созвездие без нормализации входного сигнала при выделении фазы при помощи функции atan().

Пропустив отфильтрованный I сигнал через компаратор 0/1, я получил вот такой сигнал. Он в точности соответствует тому самому бинарному сообщению 0x815F, которым был промодулирован исходном BPSK сигнал.

Это значит, что сама по себе реализация Costas Loop работает. Вот отчет, что мой модульный тест на BPSK encode decode успешно проходит.

Такие получились осциллограммы основных переменных цепи, I, Q, фаза гетеродина и сами данные.

Проверка на реальной записи с диктофона

Я программно сгенерировал *.wav файл, который непрерывно и циклически передаёт только одно слово 0x55AF на несущей звуковой частоте 1kHz. Вот так выглядит BPSK сигнал на диктофонной записи. На глаз даже и на скажешь, что это фазовая модуляция.

Затем я воспроизвел этот *.wav файл на одном мобильном телефоне и записал диктофоном на другой телефон. Затем, записанный *.wav я подал, как аргумент своей консольной утилите bpsk_demodulator.exe и она сумела выделить биты данных! Вот такое получилось сигнальное созвездие.

Пятно в центре - это пауза между сигналами. А это декодированный звук. Как можно заметить, битовая скорость была поставлена 16 бит/с.

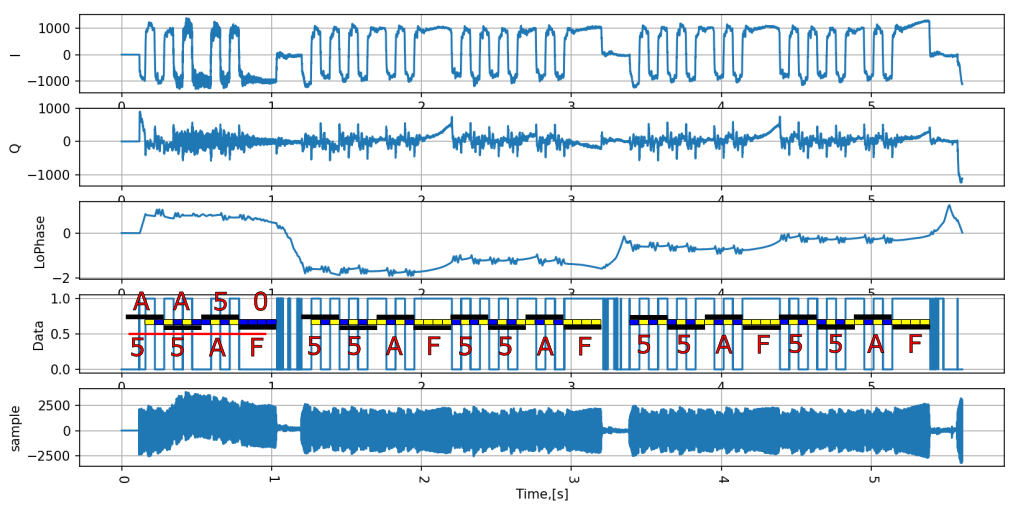
Можно заметить, что данные 0x55AF извлекаются. Хотя изначально система управления даже захватила инвертированные биты. Как с этим бороться пока не ясно. Видимо это задача протокола канального уровня. Однако в общем, можно сказать, что всё получилось. Байты передаются и принимаются через звук!

Дальнейшее развитие

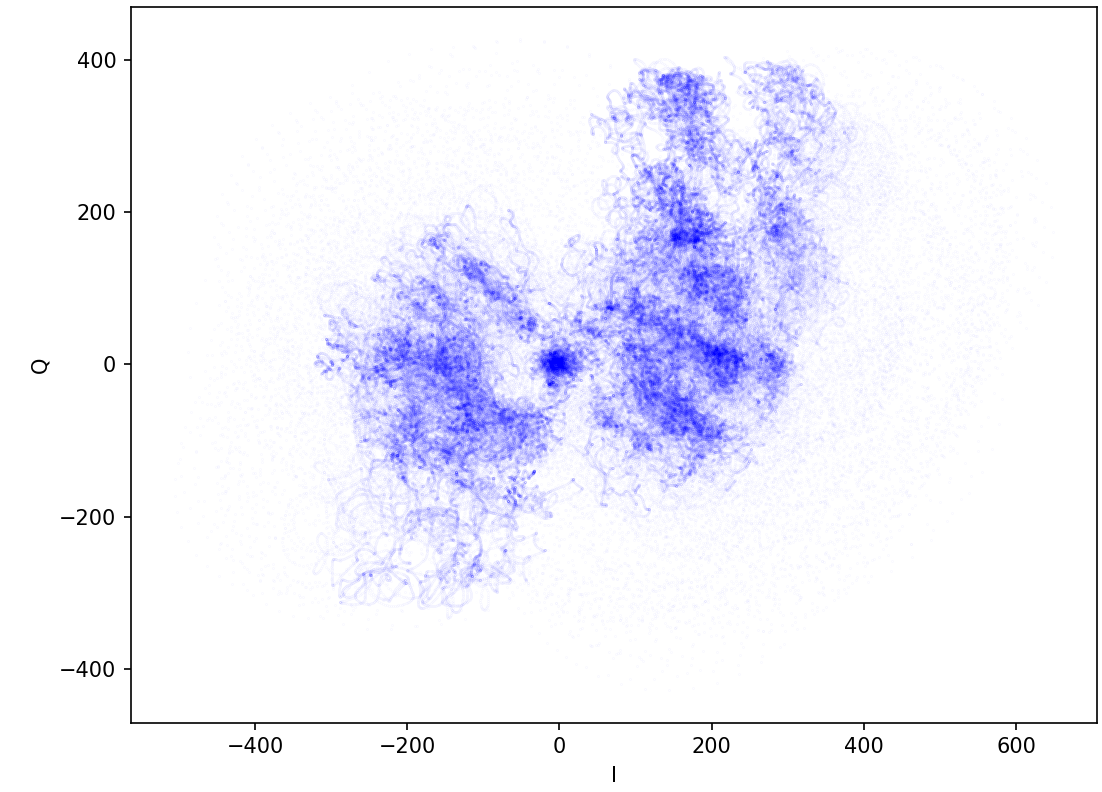
--Можно повышать битовую скорость и попытаться понять предел пропускной способности. Пока мой рекорд 50 bit/s на расстоянии 1 метр.

На битовой скорости 50 bit/s сигнальное созвездие вырождается в какое-то газовое облако.

--Было бы здорово сделать FPGA или даже ASIC, который в реальном времени сможет декодировать акустический BPSK и выдавать в SPI сырые данные m(t), которые он снял из BPSK сигнала. Проблема в том что каждый семпл надо успеть рассчитать за 1/44100Hz = 22.676 us. Самое ёмкое в вычислениях это два FIR фильтра нижних частот порядка 100...200.

--Можно вообще в одном *.wav файле записать несколько каналов BPSK на разных несущих частотах.

--Можно даже попробовать запустить этот алгоритм на микроконтроллере. Однако тут придется решить вопрос как сделать цифровой фильтр низких частот высокого порядка способный работать в реальном времени.

--Всё это позволит встраивать функцию акустических трансиверов в мобильные телефоны передавать файлы, текст, настройку часов, контакты прямо по звуку. Можно было бы и вовсе обновлять прошивку звуком. В диктофонах без USB передавать файлы на PC модулированным звуком. Как по мне это было бы здорово.

--Ещё можно сделать гидроакустический трансивер для передачи бинарных данных под водой.

--Можно к диктофонным записям подмешивать едва слышные цифровые данные, а затем при помощи софта на PC извлекать из звука метаданные: идентифицировать оборудование, геолокацию или time stamp(ы).

--Это можно преподавать в институтах ЦОС и радиотехнику на примере обработки звука. Разбор модуляций из сырого сигнала. Как по мне это веселее, чем бездумно запускать примеры из MATLAB или ещё хуже в LabView. Те SDR алгоритмы, которые Вы напишете на Си можно будет встроить куда угодно: в микроконтроллерные прошивки, в ядро OS, в user spaсe на PC.

Итоги

Удалось научиться декодировать BPSK из wav файла. Как видите тема достаточно объёмная. Тут и ТАУ, цифровые фильтры, ПИД регуляторы, конечные автоматы, преобразование Фурье, тригонометрия, комплексные числа, радиотехника, триггер Шмитта, программирование на Cи и Python, метрология. Далее помехоустойчивое кодирование, протоколы и прочее и прочее.

Понимание процесса демодуляции BPSK модуляции например открывает дорогу для декодирования навигационных данных внутри GPS сигнала.

Теперь и вы умеете работать с BPSK и можете учить других.

Ссылки

Словарь

Вопросы:

--Как в декодированном BPSK потоке семплов найти начало бита, если уже долгое время передаются только нули (или только единицы)?

--Как бороться с тем, что в BPSK модуляции данные можно интерпретировать и принять как инвертированные биты? Как выявить последовательность инвертированных бит?

--Как в потоковом режиме нормализовать (привести к единичной амплитуде) синус разной переменной амплитуды без искажения частоты и желательно фазы?