КДПВ для этой статьи сгенерировала программа размером всего в 16 байтов. Под катом разберёмся в том, как в столь скромном объёме сумел спрятаться дракон и какие силы поддерживают его жизнь. Для лучшего понимания происходящего мы портируем эту красоту на JavaScript.
О чём речь?
Программа была опубликована её автором в 2018 году на сайте Code Golf Stack Exchange и стала самой миниатюрной среди всех конкурсантов. С технической точки зрения это исполнимый файл для MS-DOS в формате COM, который рисует «кривую дракона» и имеет при этом небольшие, даже по меркам MS-DOS, размеры.
Заглянем внутрь
Итак, вот эти 16 байтов:
14 10 19 CA D1 FA 10 DE 01 D1 CD 10 B4 0C EB F0
Дизассемблировав их мы получим следующий код:
@@forever:
adc al, 10h
sbb dx, cx
sar dx, 01h
adc dh, bl
add cx, dx
int 10h
mov ah, 0Ch
jmp short @@forever
У нас по одной инструкции безусловного перехода, загрузки константы в регистр, вызова прерывания, пять арифметических операций и полное непонимание того, как это всё работает.
К слову, этот код на ассемблере можно запустить прямо в браузере, на сайте http://twt86.co/
Ассемблер?
Небольшое введение для тех, кто с ассемблером не знаком. Здесь будет абсолютный минимум, необходимый для понимания происходящего. Для обучения ассемблеру стоит поискать более полные руководства и книги.
Программа на ассемблере это набор инструкций процессора, записанных в человекочитаемом виде. В реальных программах также будут функции, директивы и макросы, но мы обойдёмся без всего этого.
В каждой строке не более одной инструкции. После инструкции может идти однострочный комментарий, он начинается со знака «точка с запятой» (;), а перед ней — метка перехода, это идентификатор, после которого идёт двоеточием. В статье, для удобства, все метки будут начинаться с двух собак (). Во «взрослых» программах на ассемблере этот префикс используется для локальных меток, недоступных из других процедур.
Инструкция начинается с мнемоники (названия) команды процессора, после неё — 1 или 2 параметра, если они нужны. Больше двух параметров бывает редко. Аналогом ассемблерных команд в языках высокого уровня будут операторы и вызовы функций. Например, инструкция mov ah, 0Ch означает запись шестнадцатеричного числа 0x0C (12) в регистр AH и если бы ассемблер использовал Си-подобный синтаксис, то могла выглядеть как ah = 0x0C;. А инструкция jmp short @ вместе с парной меткой соответствует бесконечному циклу а-ля
do {
// ...
// Здесь все инструкции, которые расположены между ними.
// ...
} while (true);
Аргументами инструкций могут быть константы, имена регистров, адреса в памяти и выражения, составленные из их комбинаций. Нам встретятся только константы и регистры.
Регистры
Регистр это регион памяти внутри процессора, к которому можно обратиться по имени. Своеобразный аналог переменной в высокоуровневых языках.
MS-DOS была актуальна во времена 16-битных 80x86-совместимых процессоров и потому подавляющее число программ под MS-DOS регистры использует максимум 16-битные. В современных процессорах регистры бывают не только 8- и 16-, но и 32-, 64-, 128-, 256- и даже 512-битными.
В демке используются только регистры общего назначения AX, BX, CX и DX. К любой из двух 8-битных частей этих 16-битных регистров можно обратиться по отдельному имени. Для AX это будут AL и AH, для BX — BL и BH и так далее.
Ещё один регистр используется опосредствованно, это регистр флагов. Нас в этом регистре будет интересовать только флаг переноса. Если при выполнении процессором арифметической операции получится результат, не помещающийся в целевой регистр, то будет взведён этот флаг.
Прерывания
Основным способом общения с окружающим миром для DOS-программ был вызов прерываний процессора, которые обслуживались обработчиками BIOS, DOS или резидентных программ.
Прерывания чем-то похожи на стандартные библиотеки в современных языках программирования. Каждое прерывание, всего их 256, предоставляет программисту некий набор функций, который тот может вызывать. Чаще всего функции логически сгруппированы. Например, большинство функций прерывания 10h посвящены работе с экраном.
Главным источником информации о существующих функциях прерываний для многих был «Список прерываний Ральфа Брауна». Одну из онлайн-версий списка можно найти здесь: http://www.ctyme.com/rbrown.htm
В коде мы встретим использование двух функций прерывания 10h, одна для перехода в графический режим и другая для рисования пикселя на экране.
На этом покончим с ассемблером и перейдём к коду демки.
Неинициализированные переменные
Как нетрудно заметить, здесь нет инициализации регистров начальными значениями перед использованием и потому мы будем полагаться те значения, которые оставила в них MS-DOS перед запуском программы.
Сайт sizecoding.org любезно подсказывает нам, что значения регистров AX и BX равны нулю, CX равен 255, а значение регистра DX совпадает со значением регистра CS. Значение сегментного регистра CS зависит от того, в какую область памяти операционная система загрузила нашу программу перед запуском и для нас это просто какое-то случайное число.
Флаг переноса в регистре флагов по умолчанию сброшен.
Будем считать, что в начале неявно присутствует блок инициализации:
mov ax, 0
mov bx, 0
mov cx, 0FFh
mov dx, 0
clc
Переход в графический режим
Командный интерпретатор MS-DOS работает в текстовом режиме экрана и первое, что нужно сделать нашей демке после запуска это переключиться в графический режим.
Чуть ниже мы видим вызов прерывания 10h при помощи инструкции int 10h. Это прерывание «специализируется» на работе с экраном, а то, какая конкретно функция будет вызвана зависит от значения регистра AH.
Регистр AX, частью которого является регистр AH, в начале работы равен 0, а значит прерывание вызовет функцию смены режима. Номер режима передаётся в регистре AL.
Первая инструкция в программе adc al, 10h, «Add With Carry» увеличивает значение регистра AL на 17 если флаг переноса взведён и на 16, если сброшен. Сразу после запуска программы флаг переноса сброшен, а значит будет установлен графический режим номер 16. В нашем распоряжении экран 640×350 пикселей и 16-цветная палитра.
Сразу после первого вызова прерывания инструкция mov ah, 0Ch меняет значение регистра AH на 0Ch и все последующие вызовы прерывания будут приводить к вызову функции рисования пикселя на экране.
Для улучшения читаемости вынесем переход в графический режим из цикла. После такого рефакторинга программа полностью сохранит своё поведение, но вырастет почти вдвое:
; Явная инициализация переменных.
mov ax, 0
mov bx, 0
mov cx, 0FFh
mov dx, 0
clc
; Переход в графический режим 640*350*16.
mov ah, 0h
mov al, 10h
int 10h
; Теперь вызов int 10h будет приводить к рисованию пикселя на экране.
mov ah, 0Ch
; Основной цикл.
@@forever:
adc al, 10h
sbb dx, cx
sar dx, 01h
adc dh, bl
add cx, dx
int 10h
jmp short @@forever
Основной цикл
После перехода в графический режим программа будет в бесконечном цикле выводить точки на экран до тех пор, пока пользователь не закроет DOSBox или не перезагрузит компьютер. Шестнадцать байтов это слишком мало для того, чтобы останавливаться.
Вычисления в основном цикле выглядят пугающе лаконичными, попробуем налить воды.
Первая инструкция, adc al, 10h прибавляет к значению регистра AL число 16 (10h), есле флаг переноса сброшен и 17 (10h + 1), если взведён.
Одна ассемблерная инструкция таила в себе целый блок if ... else .... Запишем это явно:
; adc al, 10h
jnc @@1
add al, 17
jmp @@2
@@1:
add al, 16
@@2:
Следующая инструкция, sbb dx, cx также зависит от значения флага переноса, но не прибавляет, а вычитает одно значение из другого:
; sbb dx, cx
jnc @@3
sub dx, cx
dec dx
jmp @@4
@@3:
sub dx, cx
@@4:
И снова инструкция adc, но на этот раз ситуация интереснее. Команда имеет вид adc dh, bl и прибавляет к значению регистра DH либо значение регистра BL, либо значение регистра BL плюс единица.
В регистре BL у нас нуль, а значит здесь у нас блок if без else. Значение регистра DH увеличивается на единицу только тогда, когда взведён флаг переноса.
Это единственная инструкция, где используется DH, половина от регистра DX, во всех остальных местах оный используется целиком. Нам будет удобнее, если регистр DH по-просту исчезнет. Увеличение DH на единицу увеличивает DX на 256 (28), воспользуемся этим фактом.
; adc dh, bl
jnc @@5
add dx, 256
@@5:
После этого идёт вызов функции рисования пикселя через прерывание 10h. Координата X передаётся в регистре CX, координата Y — в DX, а цвет пикселя — в AL.
Посмотрим на промежуточный результат:
; Явная инициализация переменных.
mov ax, 0
mov bx, 0
mov cx, 0FFh
mov dx, 0
clc
; Переход в графический режим 640*350*16.
mov ah, 0h
mov al, 10h
int 10h
; Теперь вызов int 10h будет приводить к рисованию пикселя на экране.
mov ah, 0Ch
; Основной цикл.
@@forever:
; adc al, 10h
jnc @@1
add al, 17
jmp @@2
@@1:
add al, 16
@@2:
; sbb dx, cx
jnc @@3
sub dx, cx
dec dx
jmp @@4
@@3:
sub dx, cx
@@4:
sar dx, 01h
; adc dh, bl
jnc @@5
add dx, 256
@@5:
add cx, dx
int 10h
jmp short @@forever
Поработаем декомпилятором
В раздувшейся в три раза программе стали проступать детали алгоритма. Перейдём на более высокий уровень абстракций и портируем код на JavaScript. Трансляция будет довольно прямолинейной, а потому остановимся только на интересных моментах.
Для начала заменим имена регистров на более понятные. Регистр CX станет переменной X, регистр DX — переменной Y, именно в таком качестве их интерпретирует функция рисования точек на экране. Регистр AL назовём просто counter. Он явно выполняет какую-то ещё функцию помимо хранения цвета пикселя, но какую именно пока ещё не ясно.
За переполнением разрядной сетки и флагом переноса нам придётся следить самостоятельно. Значение флага переноса будем хранить в переменной flag. На примере манипуляций с регистром AL в начале цикла:
// ; adc al, 10h
// jnc @@1
if (flag) {
// add al, 17
counter = counter + 17;
// jmp @@2
} else {
// @@1:
// add al, 16
counter = counter + 16;
}
// @@2:
// Вычисляем флаг переноса
flag = counter > 255;
// Обрабатываем возможное переполнение
counter = counter % 256;
Во многих языках программирования есть разделение целочисленных типов на знаковые и беззнаковые. На уровне ассемблера такое разделение тоже есть, но живёт оно только в голове программиста. Экранные координаты неотрицательны, потому можно решить, что у переменных X и Y беззнаковый тип. Но инструкция sar dx, 01h говорит нам, что это не так. Эта команда реализует деление целого знакового числа на степень двойки, а значит переменные X и Y у нас будут тоже со знаком. В языках с Си-подобным синтаксисом эта операция обозначается как :
// sar dx, 01h
Y = Y >> 1;
При этом нельзя забывать про значение флага переноса. Мнемоника sar расшифровывается как «Shift Arithmetically Right» и реализует деление через побитовый сдвиг. Инструкция sar dx, 01h сдвинет все разряды числа на один разряд вправо, освободившийся слева разряд заполнит знаком числа (1 для чисел меньше нуля и 0 для всех остальных), а самый младший разряд «вытолкнет» во флаг переноса. Иными словами, при делении чётного числа на 2 флаг переноса будет всегда сброшен, а при делении нечётного — взведён. Целиком трансляция этой инструкции будет выглядеть так:
// sar dx, 01h
flag = (Y % 2 != 0);
Y = Y >> 1;
Знаковый тип при вычислении экранных координат дарит нам последний пункт заслуживающий внимания в этой главе. Инструкция add cx, dx очень скучно и прямолинейно транслируется в X = Y + X. Но, флаг переноса, снова он!
Для представления отрицательных значений целых чисел в памяти ЭВМ используется дополнительный код. N-битная переменная может хранить значения от 0 до 2N — 1 для беззнакового числа и от -(2N — 1) до (2N — 1) — 1 для знакового. Для шестнадцатибитных целых типов это соответствует диапазонам [0..65535] и [-32768..32767] соответственно. Представление 16-битного знакового значения -32768 на двоичном уровне совпадает с беззнаковым 65536 - 32768 = 32768, а знаковое значение -1 — с беззнаковым значением 65536 - 1 = 65535.
Этой информации достаточно для вычисления флага переноса:
- Если оба слагаемых неотрицательны, то флаг сброшен
- Если оба слагаемых отрицательны, то флаг взведён
- Если знаки слагаемых не совпадают, то нужно решить неравенство
(65536 - Math.abs(Math.min(X, Y))) + Math.max(X, Y) >= 65536
Вызов прерывания, рисующий точку на экране, заменим на вызов функции putPixel(x, y, color). Её реализацией займёмся позднее.
Собрав всё воедино приходим к такому результату:
// mov cx, 0FFh
var X = 255;
// mov dx, 0
var Y = 0;
// mov al, 10h
var counter = 16;
// clc
var flag = false;
// @@forever:
do {
// ; adc al, 10h
// jnc @@1
if (flag) {
// add al, 17
counter = counter + 17;
// jmp @@2
} else {
// @@1:
// add al, 16
counter = counter + 16;
}
// @@2:
flag = counter > 255;
counter = counter % 256;
// ; sbb dx, cx
// jnc @@3
if (flag) {
// sub dx, cx
// dec dx
Y = Y - (X + 1);
// jmp @@4
} else {
// @@3:
// sub dx, cx
Y = Y - X;
}
// @@4:
// sar dx, 01h
flag = (Y % 2 != 0);
Y = Y >> 1;
// ; adc dh, bl
// jnc @@5
if (flag) {
// add dx, 256
Y = Y + 256;
}
// @@5:
// add cx, dx
// Сначала вычисляем значение флага переноса.
if (X < 0 && Y < 0) {
flag = true;
} else if (X >= 0 && Y >= 0) {
flag = false;
} else {
flag = Math.max(X, Y) >= Math.abs(Math.min(X, Y));
}
// А теперь выполняем само сложение.
X = Y + X;
// int 10h
putPixel(X, Y, counter);
// jmp short @@forever
} while (true);
putPixel()
В функции рисования точки на экране нас интересуют некорректные значения аргументов и их обработка. Это важно, так как в коде исследуемой демки нет ни единой попытки эту корректность обеспечить.
В нашем распоряжении 16-цветная палитра и при этом в качестве значения цвета пикселя может прилететь любое значение от 0 до 255. DOS решает эту коллизию просто и изящно, игнорируя значения всех битов, кроме четырёх младших и используя последние как индекс цвета в палитре. Примерно так:
let color = COLORS[colorIndex & 0xF];
С пикселями за пределами видимой части экрана попробуем поступить аналогично, будем просто игнорировать их.

Результат получился довольно близким к оригиналу, но из левой нижней части исчез один из «хвостов» дракона. Исчезнувшая часть очень похожа на продолжение хвоста, обрезанного правой кромкой экрана.
Это наталкивает на мысль, что корректность координат DOS не проверяет, а вместо этого сразу вычисляет смещение в памяти по формуле offset = y * SCREEN_WIDTH + x и если результат меньше, чем произведение ширины экрана на его высоту, то отрисовывает пиксель.
Проверим гипотезу. Разделим координату X на ширину экрана и увеличим координату Y на полученное значение. Новой координатой X станет остаток от деления. Функция рисования пикселя ожидает неотрицательные координаты и отрицательное значение на входе будет проинтерпретировано ей как очень большое положительное. Учтём и это тоже.

Стопроцентное попадание! А вот и наша функция:
function putPixel(x, y, colorIndex) {
let unsignedX = (x < 0) ? 65536 - Math.abs(x) : x;
let unsignedY = (y < 0) ? 65536 - Math.abs(y) : y;
let realX = unsignedX % SCREEN_WIDTH;
let realY = unsignedY + Math.floor(unsignedX / SCREEN_WIDTH);
if (realX >= 0 && realX < SCREEN_WIDTH && realY >= 0 && realY < SCREEN_HEIGHT) {
context.fillStyle = COLORS[colorIndex & 0xF];
context.fillRect(realX, realY, 1, 1);
}
}
Восторгаемся драконом
Мы полностью перетащили программу из DOS в браузер и теперь можем исследовать нашего дракона.
Ссылка на JSFiddle для экспериментов: https://jsfiddle.net/Maccimo/jzsfec5h/
Для начала увеличим ширину экрана до 700 пикселей и тем самым вернём кончик хвоста дракона на его законное место в правой части экрана.

А ведь ещё у нас бывают отрицательные координаты! Увеличим ширину экрана ещё на 200 пикселей, высоту вдвое и переместим точку с координатами (0, 0) из верхнего левого угла экрана на 350 пикселей вниз и 200 вправо. После этого координаты приходящие в putPixel() больше не придётся никак преобразовывать. Приятный бонус.

Теперь мы видим драконов-близнецов во всей их красе и величии! Как оказалось, программа рисовала кривую дракона Девиса-Кнута, состоящую из двух кривых дракона Хартера-Хейтуэя, но большая часть нарисованного скрывалась за пределами экрана.
По-прежнему ничего не понятно
Мы воспроизвели оригинальное поведение демки в браузере, но ясности это не прибавило.
Самая загадочная здесь, пожалуй, переменная flag: её значение получается как побочный эффект других вычислений и при этом она играет неясную, но очень важную роль. Стоит только проигнорировать её изменчивость, сделать её константой и всегда увеличивать counter либо на 16, либо на 17 как магия разрушается, драконы исчезают и весь экран погружается во тьму.
Попробуем найти закономерность между flag и зависящим от него counter. Первые 256 значений переменной counter можно увидеть на гистограмме ниже. Если переменная flag на начало итерации имела значение true, то столбец красный, иначе — синий.
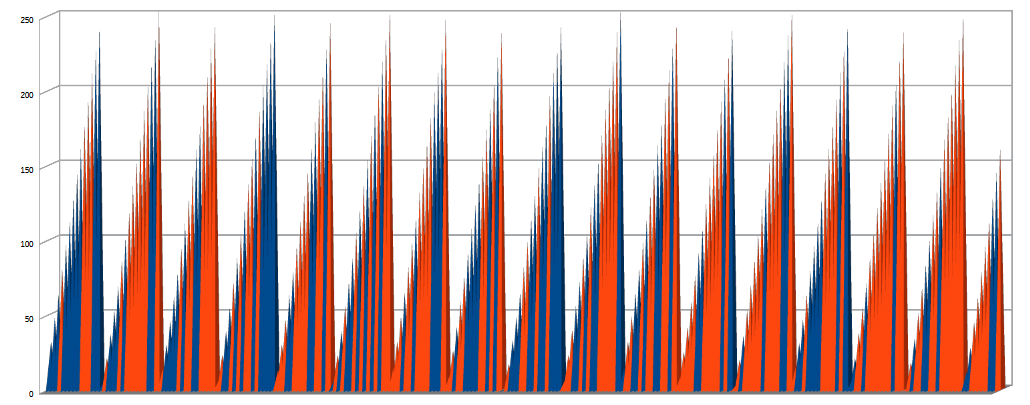
Заметили закономерность? Я тоже нет. Значения рисуют неровную пилу, устремляющуюся то выше, то ниже, но корреляции со значением flag не прослеживается. Изменения флага кажутся по-просту случайными.
Гипотеза звучит достаточно безумной, а потому достойна проверки. Заменим мудрёное вычисление флага в конце цикла на значение из генератора случайных чисел и посмотрим на результат.
flag = (Math.random() < 0.5);
Цвета отдельных пикселей поменялись, но это по-прежнему всё те же драконы-близнецы. Удивительно, но всё работает!
Это развязывает нам руки так же, как компилятору Си развязывает руки неопределённое поведение. Флаг используется в трёх местах и трижды же вычисляется его новое значение. Будем вычислять его только один раз в начале цикла.
Цвет каждого отдельного пикселя не менее случаен. Уберём переменную counter и все операции, с ней связанные, а цвет для нас будет генерировать ГПСЧ:
function randomColor() {
return Math.trunc(Math.random() * 15);
}
Избавившись от всего лишнего:
var X = 255;
var Y = 0;
do {
let flag = (Math.random() < 0.5);
if (flag) {
Y = 256 + ((Y - X - 1) >> 1);
} else {
Y = ((Y - X) >> 1);
}
X = Y + X;
putPixel(X, Y, randomColor());
} while (true);
function putPixel(x, y, colorIndex) {
context.fillStyle = COLORS[colorIndex & 0xF];
context.fillRect(x, y, 1, 1);
}
function randomColor() {
return Math.trunc(Math.random() * 15);
}
Эта версия на JSFiddle: https://jsfiddle.net/Maccimo/pkeu2b4L/
Откуда случайность?
Поискав «кривые дракона» в интернете вы найдёте сотни инструкций того, как правильно складывать пополам бесконечно длинную бумажную ленту, тысячи реализаций этого алгоритма на всех существующих языках программирования и даже узнаете про то, что дома у Дональда Кнута есть мозаичное панно, плитки для которого они с женой вылепили собственными руками. На первый взгляд случайным числам здесь места нет.
Википедия вскользь упоминает, что «фрактал может быть описан системой итерируемых функций на комплексной плоскости» и для драконов-близнецов эта система выглядит так:
Нам удобнее работать с представлением в вещественных числах, а потому приняв действительную часть параметра функции за координату y, а мнимую — за x после несложных преобразований получим эквивалентную систему уравнений:
Координаты каждой новой точки фрактала вычисляются на основе координат предыдущей. Какую именно функцию использовать для вычислений на каждом шаге выбираем случайно.
Сравним с вычислениями в коде:
Функция f4 идентична f1, функция f3 отличается от f2 на константу.
Резюмируя
В шестнадцать байтов автор сумел уместить бесконечный цикл, генератор случайных чисел, рисование точки на экране и вычисление двух пар уравнений. Распутывание этого плотно упакованного клубка инструкций было увлекательным занятием.
Математика это красиво!
Автор: Maccimo