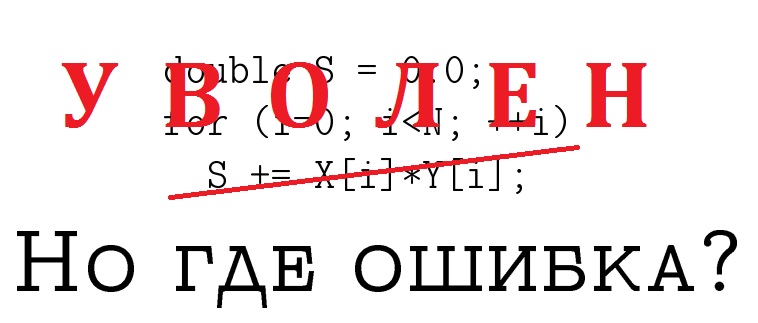Недавно на нашем ютуб-канале выступил Андрей Письменный, главный редактор Xakep.ru.
Письменный автор сотен статей, посвященных технологиям, науке и бизнесу. В роли редактора он помогал авторам обрести свой слог, оформлять идеи в связные истории.
В этом выступлении он поделится с вами опытом и приемами, которые пригодятся в работе с текстом о технологиях.
Делимся записью эфира и расшифровкой.Читать полностью »
Что-то всегда идет не по плану. Приходится отвечать на вопросы, «Что сломалось?», «Почему тормозит?» и «Почему мы не увидели этого раньше?». На примере простого приложения Даниил Галиев zefirior из Яндекс.Путешествий показал, как отвечать на эти вопросы и какие инструменты в этом помогут. Настроим логирование, прикрутим трассировку, разложим ошибки, и все это в удобном интерфейсе.
— Давайте начинать. Я расскажу об удобном логировании и инфраструктуре вокруг логирования, которую можно развернуть, чтобы вам с вашим приложением и его жизненным циклом было удобно жить. Читать полностью »
Эта статья о том, как мы совместно с роснефтёвой «дочкой» «Самаранефтехимпроект» и Казанским Федеральным Университетом в сентябре 2020 года провели «Хакатон трёх городов», на котором предложили студентам решить классическую задачу сейсмической корреляции отражающих горизонтов. С такими задачами постоянно сталкиваются специалисты по сейсморазведке по всему миру. Для участников задачу решили преподнести как «задачу поиска оптимального пути», чтобы не отпугнуть студентов страшными словами. В статье расскажем подробнее про задачу и разберём интересные решения участников. Это будет увлекательно для специалистов как по прикладному математическому моделированию, так и машинному обучению и анализу данных.
Читать полностью »
В прошлой статье речь шла о том, как можно сложить массив из чисел типа double наиболее точно, то есть получить такую сумму, как если бы мы выполняли вычисления в рамках арифметики с бесконечной точностью, а затем один раз округлили бы результат. Был показан алгоритм, который эквивалентен применению типа данных double-double, в котором сложение происходит сразу в двух переменных: основная сумма и хвостик-погрешность. Опытные читатели сразу догадались, что сложение хвостиков-погрешностей также допускает по отношению к себе рекурсивное применение того же алгоритма, что приводит не к удвоенной, а к утроенной точности, и вообще, можно организовать каскад сложений произвольного размера, получая любую наперёд заданную точность расчётов, поэтому фактически в прошлой статье была показана предпосылка к так называемой «дробной длинной арифметике». Опытный программист без труда разберётся как её реализовать, ну а я обещал дать аналогичные фундаментальные основы для скалярного произведения и вычисления полинома в точке. Поскольку все базовые вводные слова уже были сказаны в двух предшествующих статьях, в этой будет меньше «воды» и «лишних», по мнению опытных математиков, сведений. Прошу под кат.
Компания Lenovo в своё время почти ушла с рынка смартфонов, уступив место Motorola. С тех пор китайский гигант пытается вернуться, но пока у него это не очень хорошо получается.
Пока у одних компаний кризис и снижение рыночной капитализации, Tesla становится все дороже. Только за один день – пятницу – акции детища Илона Маска (Elon Musk) прибавили в цене 2,05% и достигли отметки в 585,76 долларов. Это, в свою очередь, подтолкнуло рыночную капитализацию Tesla за отметку в 555 миллиардов долларов.
