Архив за 26 апреля 2019 - 3

Введение

Английское слово wavelet (от французского «ondelette») дословно переводится как «короткая (маленькая) волна». В различных переводах зарубежных статей на русский язык встречаются еще термины: «всплеск», «всплесковая функция», «маловолновая функция», «волночка» и др.

Вейвлет-преобразование (ВП) широко используется для анализа сигналов. Помимо этого, оно находит большое применение в области сжатия данных. ВП одномерного сигнала – это его представление ввиде обобщенного ряда или интеграла Фурье по системе базисных функций.

, (1)

сконструированных из материнского (исходного) вейвлета , обладающего определенными свойствами за счет операций сдвига во времени ( b ) и изменения временного масштаба (a).

Множитель обеспечивает независимость нормы функций (1) от масштабирующего числа (a). Для заданных значений параметров a и b функция и есть вейвлет, порождаемый материнским вейвлетом .

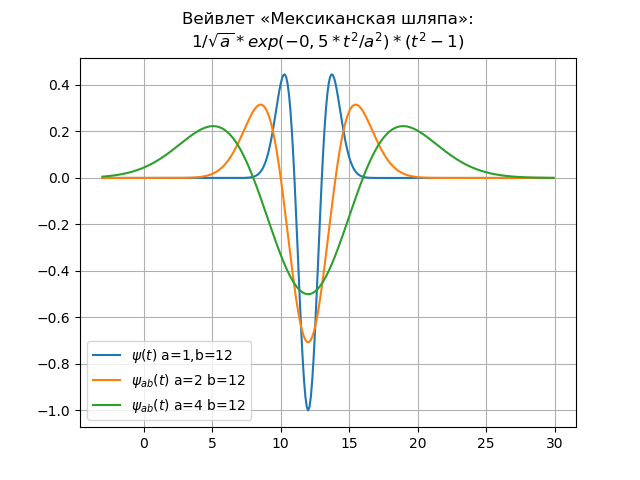
В качестве примера приведём вейвлет «мексиканская шляпа» во временной и частотной областях:

from numpy import*
import matplotlib.pyplot as plt
x= arange(-4,30,0.01)
def w(a,b,t):    
    f =(1/a**0.5)*exp(-0.5*((t-b)/a)**2)* (((t-b)/a)**2-1)
    return f
plt.title("Вейвлет «Мексиканская шляпа»:n$1/sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$")
y=[w(1,0,t) for t in x]
plt.plot(x,y,label="$psi(t)$ a=1,b=12") 
y=[w(2,12,t) for t in x]
plt.plot(x,y,label="$psi_{ab}(t)$ a=2 b=12")   
y=[w(4,12,t) for t in x]
plt.plot(x,y,label="$psi_{ab}(t)$ a=4 b=12")   
plt.legend(loc='best')
plt.grid(True)
plt.show()

Читать полностью »