Люди удивительно хорошо умеют обманывать самих себя, поэтому исследователям часто не удается воспроизвести результаты проведенных экспериментов. Об этой достаточно крупной проблеме в науке говорить не принято.
Даже самый честный человек – мастер самообмана. Мы умеем быстро выделять аномальные результаты, однако часто принимаем на веру все, как нам кажется, «логичные» выводы. Таким образом, мы бессознательно уходим от реальности.Читать полностью »
Раньше мы уже искали необычные модели Playboy с помощью библиотеки Python Scikit-learn. Теперь мы продемонстрируем некоторые возможности библиотек SymPy, SciPy, Matplotlib и Pandas на живом примере из разряда занимательных школьных задач по математике. Цель — облегчить порог вхождения при изучении Python библиотек для анализа данных.
Привет!
В прошлом году мы запустили игру для программистов CodeBattle. Напомню, идея игры очень простая: вам и сопернику дается задача, вы решаете её на выбранном вами языке. Вы видите код соперника в реальном времени, результаты запуска тестов и можете общаться с ним и зрителями в чате. Кто первый решит задачу (удовлетворит тестам) — тот победил.
С тех пор были сыграны тысячи игр, и мы собрали интересную статистику. По состоянию на 31 декабря 2015 года, какие страны и какие языки программирования чаще побеждали?
Иными словами, мы наконец можем ответить на вопрос «какой язык круче?» :) Шучу-шучу, давайте не холиварить. Вот статистика за три последних месяца прошлого года:
В лингвистике сосуществуют две традиции описания языка: одна из них, до сих пор продолжающая традицию шумеров и древних греков, описывает язык фрагментарно — отдельно фонетику и фонологию, отдельно морфологию, отдельно синтаксис и т. д. Другая, идущая с четвертого — пятого веков до н. э. от индийского монаха Панини, описывает язык как интегральное целое — описание фонетики, морфологии, синтаксиса, семантики строится в виде взаимно ориентированных правил, с помощью которых из элементарных языковых единиц строятся тексты.
Именно последний способ описания языка используется в сложнейших инженерно-лингвистических моделях, позволяющих автоматически переводить тексты одного языка на другой. О них и об их развитии и пойдёт речь на лекции.
Лектор Александр Николаевич Барулин — сотрудник Института языкознания РАН. Закончил отделение структурной и прикладной лингвистики филологического факультета МГУ им. М. В. Ломоносова. Учился в аспирантуре Института востоковедения АН СССР, защитил диссертацию на тему «Теоретические проблемы описания турецкой именной словоформы» (1984). Проработал в Институте востоковедения 12 лет. В 1991 году совместно с В. К. Финном и Д. Г. Лахути организовал факультет информатики РГГУ и возглавил созданное на этом факультете отделение теоретической и прикладной лингвистики. В 1992 по проекту Барулина был организован факультет теоретической и прикладной лингвистики — он стал деканом этого факультета, а также заведующим кафедрой теоретической и прикладной лингвистики.
Под катом — подробная расшифровка лекции.
Читать полностью »
Развлекитесь: три одинаковых цилиндра, длиной больше диаметра, взаимно перпендикулярно пересекаются своими осями в одной точке.
То же другими словами: оси координат сделали толстыми-толстыми, круглыми:
?: не пользуясь софтом и справочниками — нарисовать от руки или кратко описать словами форму области пересечения (скрыта шаром на рис. выше).
Спасибо всем участникам нашего последнего конкурса по программированию! Публикуем окончательные, исправленные результаты конкурса.
Мы получили 408 решений от 237 различных участников (в конкурсе участвует только одно, последнее из решений от каждого участника, и мы публикуем именно последние варианты). Кроме того, 14 решений было отправлено нам либо после окончания срока приёма работ, либо сотрудниками Hola, и мы рассмотрели их вне конкурса.
64 решения, или 16% от общего числа, были отправлены в течение последних суток до окончания срока. Из них 15 были отправлены в течение последнего часа, а самое последнее «проскочило» за 34 секунды до дедлайна.
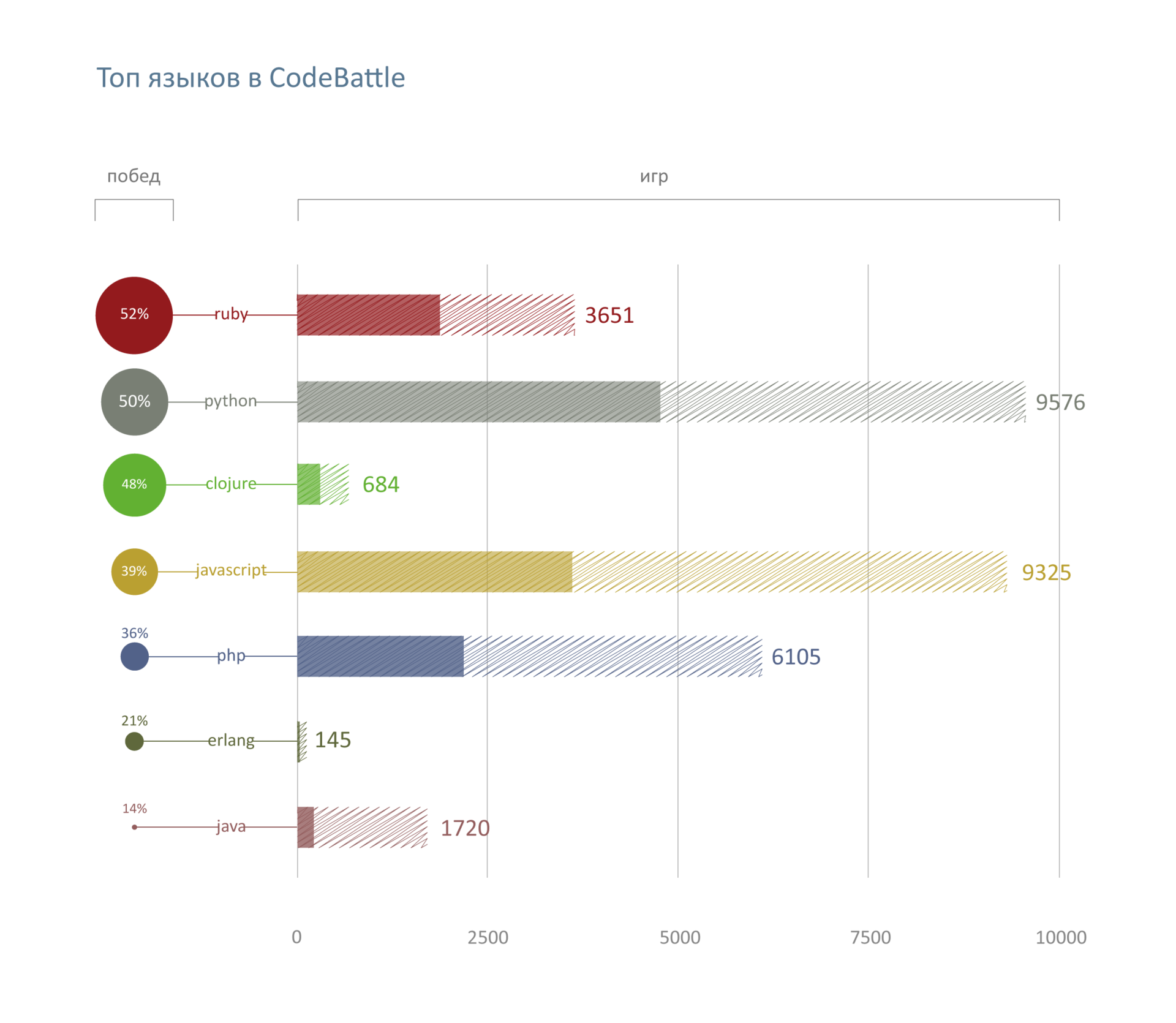
Тесты на корректность прошли 92 программы, что составляет 39% от числа протестированных. Кроме того, корректными признаны 10 из внеконкурсных решений.
Самое короткое решение уместилось ровно в 666 байт, а самое длинное растянулось на 90274 байт.
Один из участников был дисквалифицирован за попытку обмануть тестовую систему. Забавно, что его результат всё равно уступил честным результатам победителей конкурса. Ещё один участник прислал решение с говорящим названием volkswagen.js: оно работает медленно, но корректно при малом размере входных данных, и быстро выдаёт фальшивые результаты при большом размере.
Поздравляем победителей:
Читать полностью »
Спасибо участникам конкурса по программированию за долготерпение. Я пишу этот пост, чтобы признать и исправить серьёзную ошибку, которую мы допустили при подведении итогов.
Мы получили множество замечаний о методике тестирования решений. Ниже наши ответы на эти замечания.
Спасибо двоим участникам конкурса, приславшим дополнения к нашему набору тестов на корректность. Благодаря этим дополнениям нам удалось выявить несколько решений, выдающих неправильные результаты в редких случаях.
При решении задач комбинаторики часто возникает необходимость в расчете биномиальные коэффициентов. Бином Ньютона, т.е. разложение 
также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы: 
или использовать рекуррентную формулу:
Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа.
Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов не очень сложной задачей для программирования.
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Читать полностью »
Спасибо всем участникам нашего последнего конкурса по программированию!
Мы получили 408 решений от 237 различных участников (в конкурсе участвует только одно, последнее из решений от каждого участника, и мы публикуем именно последние варианты). Кроме того, 7 решений было отправлено нам либо после окончания срока приёма работ, либо сотрудниками Hola, и мы рассмотрели их вне конкурса.
Читать полностью »
Преимущество подхода на основе эллиптических кривых в сравнении с задачей факторизации числа, используемой в RSA, или задачей целочисленного логарифмирования, применяемой в алгоритме Диффи-Хеллмана и в DSS, заключается в том, что в данном случае обеспечивается эквивалентная защита при меньшей длине ключа.
В общем случае уравнение эллиптической кривой Е в поле действительных чисел R имеет вид:
— y^2+a1*x*y+a3*y = x^3+a2*x^2+a4*x+a6
или в случае конечного кольца вычетов Z|n:
— y^2+a1*x*y+a3*y = x^3+a2*x^2+a4*x+a6 mod N
Поставим перед собой задачу визуализации эллиптической кривой.
Если эллиптическая кривая Е рассматривается в поле действительных чисел R, то построение графика можно описать, используя только знания алгебры и геометрии старших классов школы
аргументы N a1 a2 a3 a4 a6 xmin xmax
