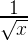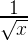«Я экспериментировал с задачами кубического представления в стиле предыдущей работы Эндрю и Ричарда Гая. Численные результаты были потрясающими…» (комментарий на MathOverflow)
Вот так ушедший на покой математик Аллан Маклауд наткнулся на это уравнение несколько лет назад. И оно действительно очень интересно. Честно говоря, это одно из лучших диофантовых уравнений, которое я когда-либо видел, но видел я их не очень много.
Я нашёл его, когда оно начало распространяться как выцепляющая в сети нердов картинка-псевдомем, придуманная чьим-то безжалостным умом (Сридхар, это был ты?). Я не понял сразу, что это такое. Картинка выглядела так:
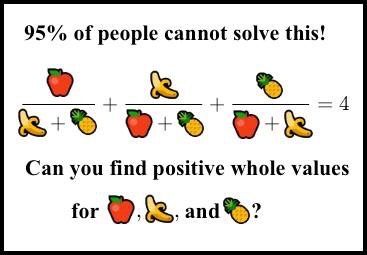
«95% людей не решат эту загадку. Сможете найти положительные целочисленные значения?»
Вы наверно уже видели похожие картинки-мемы. Это всегда чистейший мусор, кликбэйты: «95% выпускников МТИ не решат её!». «Она» — это какая-нибудь глупая или плохо сформулированная задачка, или же тривиальная разминка для мозга.
Но эта картинка совсем другая. Этот мем — умная или злобная шутка. Примерно у 99,999995% людей нет ни малейших шансов её решить, в том числе и у доброй части математиков из ведущих университетов, не занимающихся теорией чисел. Да, она решаема, но при этом по-настоящему сложна. (Кстати, её не придумал Сридхар, точнее, не он полностью. См. историю в этом комментарии).
Вы можете подумать, что если ничего другое не помогает, то можно просто заставить компьютер решать её. Очень просто написать компьютерную программу для поиска решений этого кажущегося простым уравнения. Разумеется, компьютер рано или поздно найдёт их, если они существуют. Большая ошибка. Здесь метод простого перебора компьютером будет бесполезен.
Читать полностью »