Эта изготовленная примерно в 1800-1600 годах до нашей эры глиняная табличка свидетельствует, что древние вавилоняне смогли аппроксимировать квадратный корень двух с точностью 99,9999%.
Как им это удалось?
Рубрика «Занимательные задачки» - 2
Как вавилонянам удалось вычислить √2 с точностью до шести знаков после запятой?
2023-03-07 в 12:04, admin, рубрики: Блог компании Цифровой СИБУР, вавилон, задачки, Занимательные задачки, математика, Научно-популярноеML-задача на 30 минут: гадаем по cookie
2023-01-17 в 6:00, admin, рубрики: big data, data science, machinelearning, Блог компании МТС, данные, Занимательные задачки, машинное обучение, соревнование, хакатон, Хакатоны«Я тебя по IP вычислю!» – помните такую угрозу из интернета времен нулевых годов? Мы в Big Data МТС решили выяснить, можно ли составить хотя бы приблизительное представление о человеке, обладая информацией о сайтах, которые он посещает. Для этого мы сгенерировали полусинтетические данные, чтобы понять, насколько смелыми можно быть в этих ваших интернетах.
Читать полностью »Занимательная задачка по мотивам теоремы Гёделя о неполноте
2022-11-25 в 22:00, admin, рубрики: гёдель, Занимательные задачки, ложб, математика, правда, теорема о неполноте
Альберт Эйнштейн награждает Гёделя (второй справа) наградой, названной в честь него самого
В 1931 году австрийский логик, математик и философ математики Курт Гёдель опубликовал свою теорему о неполноте. Эта работа считается одним из величайших интеллектуальных достижений современности.
В теореме утверждается, что в любой разумной математической системе всегда будут существовать истинные утверждения, которые невозможно доказать. Это утверждение шокировало математическую общественность, в которой до того преобладал неистребимый оптимизм, касающийся мощи и всеобъемлющей природы математики. Предполагалось, что математика «полна» — то есть, любое утверждение можно доказать или опровергнуть. 25-летний Гёдель показал, что это не так, составив корректное утверждение, доказать которое невозможно. Таким образом он продемонстрировал ограничения математики.
Теорема о неполноте преобразовала исследования основ математики и станет важным фактором развития информатики, поскольку из неё следует, что у возможностей всех формализованных систем, в том числе и языков программирования, есть свои ограничения.
Читать полностью »
ИТ листок
2022-11-14 в 13:51, admin, рубрики: Занимательные задачки, идея, инструменты аналитики, помощь ближнемуИдеи как побороть информационный голод в заключении
Уважаемые читатели Хабр! Всем привет!
2 2 2 2 = 7
2022-11-06 в 14:44, admin, рубрики: задачки, Занимательные задачки, логические задачи, логические игры, математикаВ общем случае задача выглядит как поиск знаков арифметических операций и иных действий без использования других цифр для того, чтобы получить из четырёх двоек любое число от 0 до 9.
Довольно простые решения на сложение, деление и возведение в степень есть для всех чисел, кроме 7.
С 7 же нужно выйти за рамки привычного (помните головоломку про соединение точек и выход из зоны квадрата). По решению задачи можно многое узнать о собеседнике.
Занимательные задачки, рождённые венгерской математической школой
2022-07-30 в 18:06, admin, рубрики: Венгрия, загадки, Занимательные задачки, кубик рубика, трёхмерная решётка
Венгрия по праву может считаться математической сверхдержавой – и не только из-за «кубика Рубика», придуманного венгром Эрнё Рубиком. В 1894 году Венгрия первой в мире начала проводить математические олимпиады для подростков – за четыре десятилетия до того, как они стали проводиться где-то ещё. В том же году там начали издавать математический журнал KöMaL для учеников средней школы, в котором содержались различные задачки и приёмы для их решения. Олимпиада и журнал существуют до сих пор, с перерывами на мировые войны.
В результате венгры постоянно придумывают различные математические загадки, и в этой стране процент высококлассных математиков выше, чем в любой другой.
Директор американской математической олимпиады, венгр Бела Байнок, поделился с редакцией The Guardian «трёхмерными логическими загадками» — в таких задачках решение нужно искать при помощи трёхмерной решётки. Он сказал, что никогда не сталкивался с такими задачками за пределами Венгрии.
Читать полностью »
Математическое решение задачи о матрице «змейкой»
2022-06-18 в 21:14, admin, рубрики: c++, Алгоритмы, Занимательные задачки, Лайфхаки для гиков, математика, математика для программистов, Программирование, условия, циклыНастоящая статья продолжает тему предыдущей работы (https://habr.com/ru/post/560266/Читать полностью »
Как рисовать с помощью SQL?
2022-05-07 в 20:15, admin, рубрики: fun, mysql, sql, Занимательные задачкиВидимо я сделала какое-то очень плохое зло, поэтому живу во время перемен. Справиться с эмоциями и повысить свою конкурентоспособность на рынке Data Enigneer’ов мне помогает сайт Hackerrank. На пути к решению вообще всех задач по SQL с этого сайта мне попалась задачка на нетривиальные запросы.
В задачке требовалось звёздочками нарисовать прямоугольный треугольник.
Понятно, что можно было сделать как-то так:
SELECT '*'
UNION ALL
SELECT '* *'
UNION ALL
...Но это дико скучно и некрасиво.
Давайте разберемся, как рисовать с помощью SQL, и при этом ощущать себя настоящим творцом!Читать полностью »
Интеллектуальный брутфорс: пишем головоломку и солвер для неё
2022-04-30 в 18:39, admin, рубрики: Rust, Блог компании Билайн Бизнес, головоломка, Занимательные задачки, игры, Игры и игровые консоли, информационная безопасность, Программирование, разработка игр
Небольшое предисловие
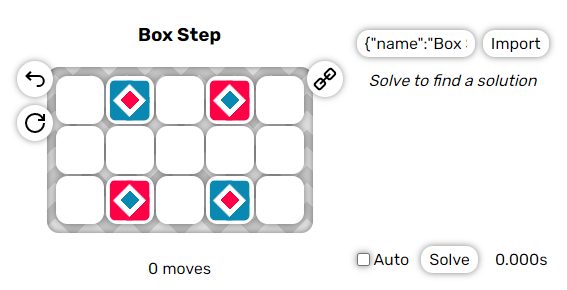
В колледже я много играл в головоломки. В статье под головоломками я буду подразумевать очень узкое подмножество таких игр. Вот некоторые из примеров:
Также мне посчастливилось изучать структуры данных в Политехническом институте Ренсселера, где в то время студенты профессора Катлера (привет, Барб!) ежегодно участвовали в соревновании по написанию солвера головоломок. Каждый год игра менялась, и в мой год это была Ricochet Robots, которая по сути является головоломкой со скольжением по льду для нескольких игроков. Мне очень понравилось это задание (и я победил в соревновании!), после чего я продолжил участвовать в соревнованиях в качестве ассистента преподавателя.
Цель этой задачи заключалась в том, чтобы познакомить всех с рекурсией и поиском в глубину. Программе передавались исходное состояние игры, а также максимальная глубина рекурсии. Необходимо было вернуть или кратчайшее решение или все возможные решения минимальной длины. В соревнованиях игрокам могли или сообщать, или не сообщать предел глубины; кроме того, возможны были головоломки, не имеющие решения. Я многому научился и получил кучу удовольствия, так что, возможно, вам это тоже понравится.
Читать полностью »