Предлагаю переработанный вариант своего выступления на конференции разработчиков, в котором я решил отвлечься от фреймворков-технологий и порассуждать на тему сопоставимости в разработке.
Под катом слайды с пояснением.
Читать полностью »
Рубрика «закон Бенфорда»
Как эмпирическое правило «победитель получает все» работает и не работает в разработке
2017-10-03 в 4:17, admin, рубрики: Алгоритмы, Винни Пух, выбросы, вычислительная математика, Гауссиана, Дробные производные, закон Бенфорда, Заря Программирования, Зевс, Коши, Леви, математика, оптимизация, производительность, скоро зима, Совершенный код, Солнечная система, статистика, фракталы, Хинчин, ЧебышевЗакон Бенфорда и распределения под него попадающие
2014-10-19 в 15:06, admin, рубрики: big data, бесконечная дисперсия, борьба с фальсификациями, закон Бенфорда, математика, математическая статистика, Научно-популярное, правило первой цифры, скоро зима, списки стран, теория вероятностей, устойчивое распределение
В теории вероятностей и статистике правило первой цифры, или закон Бенфорда, показывает любопытное проявления частот первой цифры данных из реальной жизни. Для школьников и домохозяек этот закон можно вольно сформулировать так: есть наборы данных, у которых первая цифра будет единицей примерно в 6 раз чаще, чем девятка и это соотношение не изменится при масштабировании исходного набора. Более строго можно сформулировать так: набор чисел удовлетворяет закону Бенфорда, если первая цифра d появляется с вероятностью
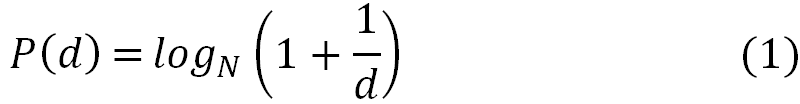
Здесь N – основание системы счисления, должно быть больше 2, далее будем рассматривать 10.
Для строгих математиков это правило формулируется так: существуют такие случайные величины, для которых распределение вероятностей дробной части логарифма по любому основанию большему 1 сходится к равномерному на отрезке [0; 1] распределению. Далее я постараюсь писать как можно популярнее и подробнее, укажу примеры, ограничения, применение и случайные величины, для которых закон применим.
Читать полностью »