3 июня 2014 г. в Санкт-Петербургском государственном экономическом университете (СПбГЭУ) прошла уже вторая по счету Российская конференция Wolfram технологии, в которой мне посчастливилось участвовать в качестве одного из докладчиков.
К слову сказать, первая конференция проходила там же годом ранее, 13 июня 2013 г., причем открывал ее лично сам Стивен Вольфрам, CEO компании Wolfram Research (выступления и презентации той конференции вы можете найти здесь). Первая конференция была знаковым событием, ее посетило множество людей и на протяжении 3-х с лишним часов участники конференции не отпускали Стивена, задавая ему все новые и новые вопросы, касавшиеся то Wolfram|Alpha, то фундаментальных основ Mathematica, то темы, которой Стивен Вольфрам занимается очень давно — клеточных автоматов.
Думаю ни для кого не секрет, что компания уже скоро выпустит 10-ю версию системы Mathematica, которая, по моему глубокому ощущению, станет если уж не самым, то одним из самых мощных скачков Mathematica. Сейчас, когда я пишу эти строки, код системы уже заморожен и уже во всю ведется подготовка к релизу. О языке Wolfram, который является также языком всех продуктов Wolfram, на Хабрахабре уже шла речь, скажем в переводе на русский язык выступления Стивена на SXSW 2014, также этому языку была посвящена и большая доля конференции. Думаю многим будет интересно также, что сейчас стартовал конкурс "Выиграй Mathematica 10", победитель которого получит 10-ю версию сразу после релиза.
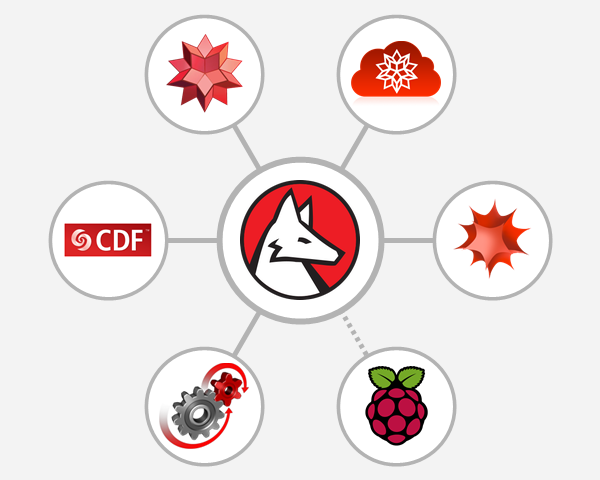
На картинке в начале этой заметки (см. Дополнение 1 в конце) вы можете видеть те продукты Wolfram, о которых на ней шла речь. Это, собственно, Язык Wolfram, его главные носители — Mathematica 10, Облако Wolfram и Wolfram|Alpha, а также ряд других продуктов, таких как CDF, SystemModeler и Raspberry Pi. Ссылка к Raspberry идет пунктиром потому что это, безусловно, не продукт Wolfram, но с ноября 2013 г. язык Wolfram и Mathematica предустановлены на этих одноплатных компьютерах, причем это бесплатно.
Читать полностью »