Рубрика «wolfram language» - 7

в 10:32, , рубрики: wolfram language, wolfram mathematica, математика, Программирование, тернарные деревья, фрактал, фрактальные деревья

Приключения в математическом лесу фрактальных деревьев

Перевод поста Bernat Espigulé Pons, «Adventures into the Mathematical Forest of Fractal Trees».
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь.

Без сомнения, золотое сечение и в наше время представляется одним из самых таинственных, волшебных и поразительных чисел, которые известны людям: 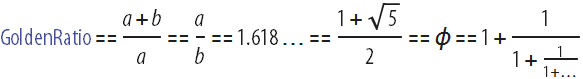Prikljuchenija-v-matematicheskom-lesu-fraktalnyh-derevev_1.png. (в языке Wolfram Language и системе Mathematica ему соответствует символ GoldenRatio). Как вы увидите из этого поста, это число действительно имеет множество интересных свойств, которые можно исследовать, причём некоторые из них рассматривались ещё в работах учёных Древней Греции, таких как Пифагор и Евклид, другие в работах итальянского математика Леонардо Пизанского, более известного под прозвищем Фибоначчи, или Иоганном Кеплером — астрономом эпохи Возрождения. Хотя это может прозвучать странно, в этом посте я расскажу вам о новых геометрических объектах, связанных с золотым сечением, которые осветили мне путь, когда я пытался отобразить неизвестную ранее область Математического Леса.
Читать полностью »

в 8:25, , рубрики: mathematica, wolfram language, математика, приближенное решение, Программирование, точное решение, триангуляция

Переход от приближенного решения к точному: задача о разбиении квадрата на 50 подобных остроугольных треугольников

Перевод поста Эда Пегга младшего (Ed Pegg Jr) "From Close to Perfect—A Triangle Problem"
Выражаю благодарность за помощь в переводе Андрею Дудину.
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь.

В языке Wolfram Language (доступном, скажем, в системе Mathematica) функция RootApproximant позволяет найти замкнутую форму в виде алгебраического числа для некоторого приближённого числа, и эта функция позволила нам превратить приближенное решение задачи о разбиении квадрата на 50 подобных остроугольных треугольников с углами (45°, 60°, 75°) в точное.

Ясно, что квадрат можно разбить на треугольники (триангулировать), например, просто соединив его противоположные вершины. Известно, так же, что квадрат можно разбить на семь подобных треугольников разной площади или на десять остроугольных равнобедренных треугольников (см. рис. ниже). Известны также классические задачи, связанные с разбиением квадрата на восемь остроугольных треугольников (см. рис. ниже), или на двадцать треугольников со сторонами, относящимися друг к другу как Perehod-ot-priblizhjonnogo-reshenija-k-tochnomu-zadacha-o-razbienii-kvadrata-na-50-podobnyh-ostrougolnyh-treugolnikov_1.png. На третьем чертеже (считая сверху) показано разбиение квадрата на подобные треугольники с углами (45°, 60°, 75°), но вы можете с легкостью заметить, что это решение не корректно, так как один из треугольников немного накладывается на другой.
Читать полностью »

в 6:46, , рубрики: twitter, wolfram language, Программирование, функциональное программирование

Компания Wolfram Research открыла сервис Tweet a Program: интересных программ на языке Wolfram Language, длина которых не превышает 140 символов

В языке Wolfram Language небольшой код может делать крайне много. Используя это, мы сделали сервис, который позволит вам получить от этого удовольствие, сегодня мы открываем его — Tweet-a-Program.

Этот сервис соединяет в себе программы на языке Wolfram Language длиной в одно сообщение твиттера и возможность их автоматической отправки в @WolframTaP. Наш Твиттер-бот запустит вашу программу в Wolfram Cloud (Облаке Wolfram), после чего опубликует результат.

Hello World from Tweet-a-Program: GeoGraphics[Text[Style["Hello!",150]],GeoRange->"World"]
Читать полностью »

в 11:04, , рубрики: Stephen Wolfram, Wolfram Alpha, wolfram language, wolfram mathematica, Исследования и прогнозы в IT, математика, Программирование, Стивен Вольфрам, метки: , , , ,

Вычисляемые знания и будущее чистой математики

Перевод поста Стивена Вольфрама (Stephen Wolfram) "Computational Knowledge and the Future of Pure Mathematics"
Выражаю огромную благодарность тем, кто помог мне сделать этот перевод: Владиславу Глаголеву (Himura), Илье Марчевскому, Сергею Шевчуку (opckSheff) и Анне Коваленко.

Введение

Уже больше века, каждые 4 года в некоторой точке мира проходит Международный конгресс математиков (ICM). В 1900 году, именно на нем Давид Гильберт представил свою знаменитую коллекцию проблем математики, которая по сей день задает направление исследования математикам всего мира.

В этом году ICM проходит в Сеуле, и сегодня я отправляюсь туда. Однажды я уже бывал на ICM — в Киото в 1990 году. Тогда системе Mathematica было всего 2 года, и математики ещё только начинали привыкать к ней. Многие уже повсеместно её использовали, но на ICM были и те, кто говорил «Я занимаюсь чистой математикой. В чем, интересно, мне может помочь система Mathematica?»

Vychisljaemye-znanija-i-budushhee-chistoj-matematiki_1.gif
Читать полностью »

в 7:25, , рубрики: Stephen Wolfram, Wolfram, Wolfram Alpha, wolfram data science platform, wolfram knoledgebase, wolfram language, wolfram research, Презентации, Программирование, Софт, метки:

Выпущена система Mathematica 10, содержащая 700+ новых функций и невероятное количество R&D
Перевод статьи Стивена Вольфрама, о системе Wolfram Mathematica 10, которая вышла 9 июля 2014 г.
Оригинальный текст вы можете найти здесь.
Выражаю огромную благодарность тем, кто помог мне перевести эту статью: Владиславe Глаголеву (Himura), Сильвии Торосян и Рукк Наталии Самуиловне.

Этим летом мы выпускаем поистине огромный спектр новых технологий. Две недели назад мы запустили Wolfram Programming Cloud. А сегодня, я рад представить вам в значительной степени обновленную версию Mathematica: Mathematica 10.

Wolfram Mathematica 10

Мы выпустили Mathematica 1 чуть более 26 лет лет назад, 23 июня 1988 г. С тех пор мы постоянно и систематично делали Mathematica еще больше, мощнее, шире, и глубже. Но Mathematica 10, выпущенная сегодня, представляет собой пожалуй самый большой скачек в функциональности за всю историю Mathematica.
Читать полностью »

в 9:32, , рубрики: Wolfram, wolfram language, wolfram mathematica, я пиарюсь, метки: , ,

Вниманию абитуриентов: в СПбГЭУ открыто новое направление «Прикладная математика и информатика» с глубоким изучением Wolfram Mathematica

Информация о направлении на сайте СПбГЭУ.

Хотели бы Вы получить профессиональное образование, всецело ориентированное на использование Wolfram-технологий? Не отдельный курс занятий, в котором преподаватель использует Wolfram Mathematica, не курсы переподготовки, а полноценное Высшее образование! И не где-нибудь, а в Санкт-Петербурге, в самом центре города. Именно такую возможность Вам представляет кафедра Экономической кибернетики и экономико-математических методов Санкт-Петербургского Государственного Экономического Университета (СПбГЭУ) – крупнейшего экономического ВУЗа, ежегодно занимающего ведущие позиции в рейтингах министерства образования.

В этом году (впервые!) кафедра ЭКиЭММ осуществляет приём на новое перспективное направление Прикладная математика и информатика со специализацией в области экономико-математических методов. Обучаясь по этому направлению, на первых двух курсах студенты получают расширенную углублённую общематематическую и компьютерную подготовку, изучая, Математический анализ, Высшую и Линейную алгебру и Аналитическую геометрию, Языки программирования высокого уровня, Дискретную математику, Дифференциальные уравнения, Компьютерные математические среды, Функциональный анализ, Теорию функций комплексного переменного, Теорию вероятностей и Математическую статистику. На старших курсах студенты изучают большой блок прикладных экономических дисциплин, в число которых входят: Теория игр, Эконометрика, Финансовая математика, Актуарная математика, Математическое моделирование, Исследование операций, Теория принятия решений, Методы прогнозирования, Модели экономической динамики, Планирование расписаний и управление доходами, Многомерный статистический анализ, Имитационное моделирование и другие дисциплины.
Читать полностью »

в 18:11, , рубрики: game development, Wolfram, wolfram language, wolfram mathematica, Программирование

Как выигрывать в игре камень ножницы бумага? (реализация оптимальной стратегии в Wolfram Mathematica)

Перевод поста Джона Маклуна (Jon Mcloone, директор департамента международного бизнеса и стратегического развития Wolfram Research). Оригинал поста: How to Win at Rock-Paper-Scissors
Скачать пост в виде документа Mathematica

С точки зрения математики игра камень-ножницы-бумага (см. Дополнение 1 в конце) не является особо интересной. Стратегия равновесия Нэша очень проста: случайно и с одинаковой вероятностью выбирайте из трех вариантов, и при условии проведения большого числа игр ни вы, ни ваш соперник не сможете одержать победу. Хотя, при обсчитывании стратегии при помощи компьютера всё ещё возможно выиграть у человека после большого числа игр.
Читать полностью »

в 3:20, , рубрики: Wolfram, Wolfram Alpha, wolfram language, wolfram mathematica, wolfram systemmodeler, wolfram workbench, Презентации, Программирование

Вторая российская конференция «Wolfram технологии»: рассказ и материалы

3 июня 2014 г. в Санкт-Петербургском государственном экономическом университете (СПбГЭУ) прошла уже вторая по счету Российская конференция Wolfram технологии, в которой мне посчастливилось участвовать в качестве одного из докладчиков.

К слову сказать, первая конференция проходила там же годом ранее, 13 июня 2013 г., причем открывал ее лично сам Стивен Вольфрам, CEO компании Wolfram Research (выступления и презентации той конференции вы можете найти здесь). Первая конференция была знаковым событием, ее посетило множество людей и на протяжении 3-х с лишним часов участники конференции не отпускали Стивена, задавая ему все новые и новые вопросы, касавшиеся то Wolfram|Alpha, то фундаментальных основ Mathematica, то темы, которой Стивен Вольфрам занимается очень давно — клеточных автоматов.

Думаю ни для кого не секрет, что компания уже скоро выпустит 10-ю версию системы Mathematica, которая, по моему глубокому ощущению, станет если уж не самым, то одним из самых мощных скачков Mathematica. Сейчас, когда я пишу эти строки, код системы уже заморожен и уже во всю ведется подготовка к релизу. О языке Wolfram, который является также языком всех продуктов Wolfram, на Хабрахабре уже шла речь, скажем в переводе на русский язык выступления Стивена на SXSW 2014, также этому языку была посвящена и большая доля конференции. Думаю многим будет интересно также, что сейчас стартовал конкурс "Выиграй Mathematica 10", победитель которого получит 10-ю версию сразу после релиза.

На картинке в начале этой заметки (см. Дополнение 1 в конце) вы можете видеть те продукты Wolfram, о которых на ней шла речь. Это, собственно, Язык Wolfram, его главные носители — Mathematica 10, Облако Wolfram и Wolfram|Alpha, а также ряд других продуктов, таких как CDF, SystemModeler и Raspberry Pi. Ссылка к Raspberry идет пунктиром потому что это, безусловно, не продукт Wolfram, но с ноября 2013 г. язык Wolfram и Mathematica предустановлены на этих одноплатных компьютерах, причем это бесплатно.
Читать полностью »

1...567
Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js