Содержание
Часть 1 — Задача двух тел
Часть 2 — Полу-решение задачи двух тел
Часть 3 — Ужепочти-решение задачи двух тел
Второй закон Кеплера
Всем привет! В прошлый раз мы остановились на вот этих уравнениях:
begin{equation*}
begin{cases}
ddot{x} = -mu dfrac{x}{(x^{2}+y^{2})^{frac{3}{2}}},
\
ddot{y} = -mu dfrac{y}{(x^{2}+y^{2})^{frac{3}{2}}}.
end{cases}
end{equation*}
Задачка теперь плоская, все будет — хорошо. Запустим численное моделирование и отрисуем несколько траекторий движения (для разных начальных условий). Не анимацию, как раньше, а чтобы видно было какие формы имеют линии:
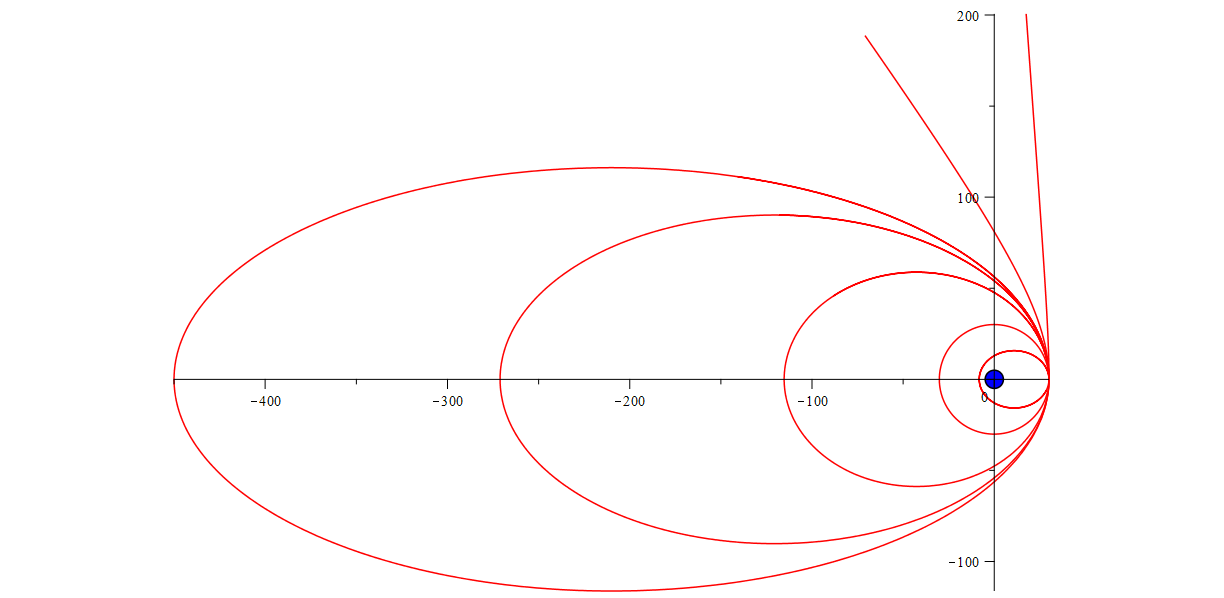
Возможные траектории движения спутника
Те кто знаком с эллипсами сразу скажут: тю, так это похоже эллипсы!
А те кто не слышал о эллипсах скажут: овал. Или сплюснутый кружок.
Читать полностью »
