Ноябрьским вечером 1999 года присяжные собрались произнести вердикт в зале Честерского суда. На скамье подсудимых – 35-летняя адвокат из Чешира по имени Салли Кларк, мать двоих умерших младенцев. За окном холодно, а внутри – мёртвая тишина. Только что эксперт-педиатр сэр Рой Мидоу спокойно сообщил ошеломляющую цифру: вероятность того, что две здоровые дети из одной благополучной семьи скончались естественной смертью, равна «примерно одному шансу из 73 миллионов»Читать полностью »
Рубрика «вероятности»
Как вероятность 1 к 73 000 000 стала приговором для матери двух младенцев: дело Салли Кларк
2025-09-30 в 18:26, admin, рубрики: вероятности, математика, судКак математика тасовки карт едва не разрушила империю онлайн-покера
2025-09-18 в 10:43, admin, рубрики: вероятности, карты, покер, тасованиеКарточные дилеры создают уникальную колоду при каждой тасовке, а компьютеры не могут это повторить
Если вы когда-нибудь перемешивали колоду игральных карт, то, скорее всего, создали тем самым уникальную колоду. То есть, вероятно, вы единственный человек, который когда-либо раскладывал карты именно в таком порядке. Хотя это утверждение звучит невероятно, оно прекрасно иллюстрирует, как быстро большие числа могут проникнуть в повседневные ситуации — иногда с серьёзными и неприятными последствиями, как обнаружили разработчики одного онлайн-покера в конце 1990-х годов.
Уточнение процентилей с помощью полиномиальной аппроксимации
2024-09-05 в 14:05, admin, рубрики: аппроксимация, вероятности, квантили, квартили, плотность распределдения, полиномы, процентили, степень полиномаКогда заказчик просит определить процентили для дискретных значений и хочет получить точные значения в виде непрерывных величинЧитать полностью »
Случайное распределение урона в RPG
2017-08-19 в 7:00, admin, рубрики: dice, вероятности, генератор случайных чисел, кости, разработка игр, распределение вероятности
Для вычисления урона от атаки в таких настольных ролевых играх, как Dungeons & Dragons, используются броски урона. Это логично для игры, чей процесс основан на бросках кубиков. Во многих компьютерных RPG урон и другие атрибуты (сила, очки магии, ловкость и т.д.) вычисляются по похожей системе.
Обычно сначала пишется код вызова random(), а затем результаты корректируются и подстраиваются под нужное игре поведение. В этой статье будут рассмотрены три темы:
- Простые корректировки — среднее значение и дисперсия
- Добавление асимметрии — отбрасывание результатов или добавление критических попаданий
- Полная свобода в настройке случайных чисел, неограниченная возможностями кубиков
Продвинутая тактика игры в «Сапёр»
2017-07-28 в 7:21, admin, рубрики: minesweeper, вероятности, сапёр, статистика, Читальный зал[Пятничный перевод статьи 1999 года одного из авторов движка игры Thief Шона Барретта]
Неприятное положение в «Сапёре»
В этом положении я знаю, что вокруг меня есть куча мин, но не могу определить, где они находятся. Несколько мин может быть в одном из двух мест (розовые или голубые), группа мин может быть расположена в одной из двух комбинаций (светло-/тёмно-зелёные). Кроме того, есть ещё сложная ситуация с «5» и «6» в левом верхнем углу, которую я никак не выделил.
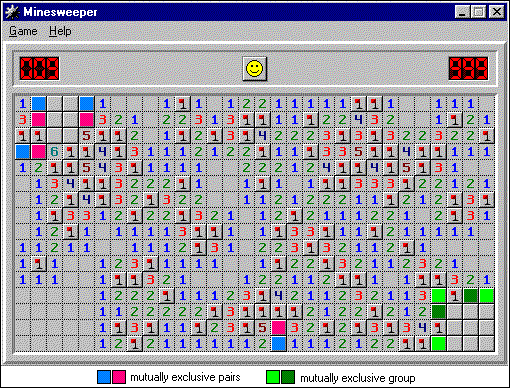
Голубые/розовые — взаимоисключающие пары, светло-/тёмно-зелёные — взаимоисключающие группы
«Сапёр»: логика или вероятность
В «Сапёра» можно играть двумя способами: как в логическую или в вероятностную игру.
Технически, вероятность подразумевает логику. Если вы можете логически доказать, что мина должна находиться в определённом месте, то вероятность равна 100%. Если можете доказать, что её в этом месте нет, то вероятность равна 0%. То есть в каком-то смысле для нас важны только вероятности. Тем не менее, игрок для распознавания таких стопроцентных ситуаций игрок использует логическую дедукцию. Иногда, особенно на низких уровнях сложности, её достаточно для прохождения уровня, никакого подсчёта вероятностей не требуется.
Но бывают такие ситуации, когда вся логика мира не может вас спасти. Простой пример — ситуация с «T», которую видно внизу по центру. Она немного осложняется дополнительными соседними минами. (В простейшем случае «2» заменяется на «1», а «5» — на «3», чтобы ситуация была симметричной.)
Читать полностью »
