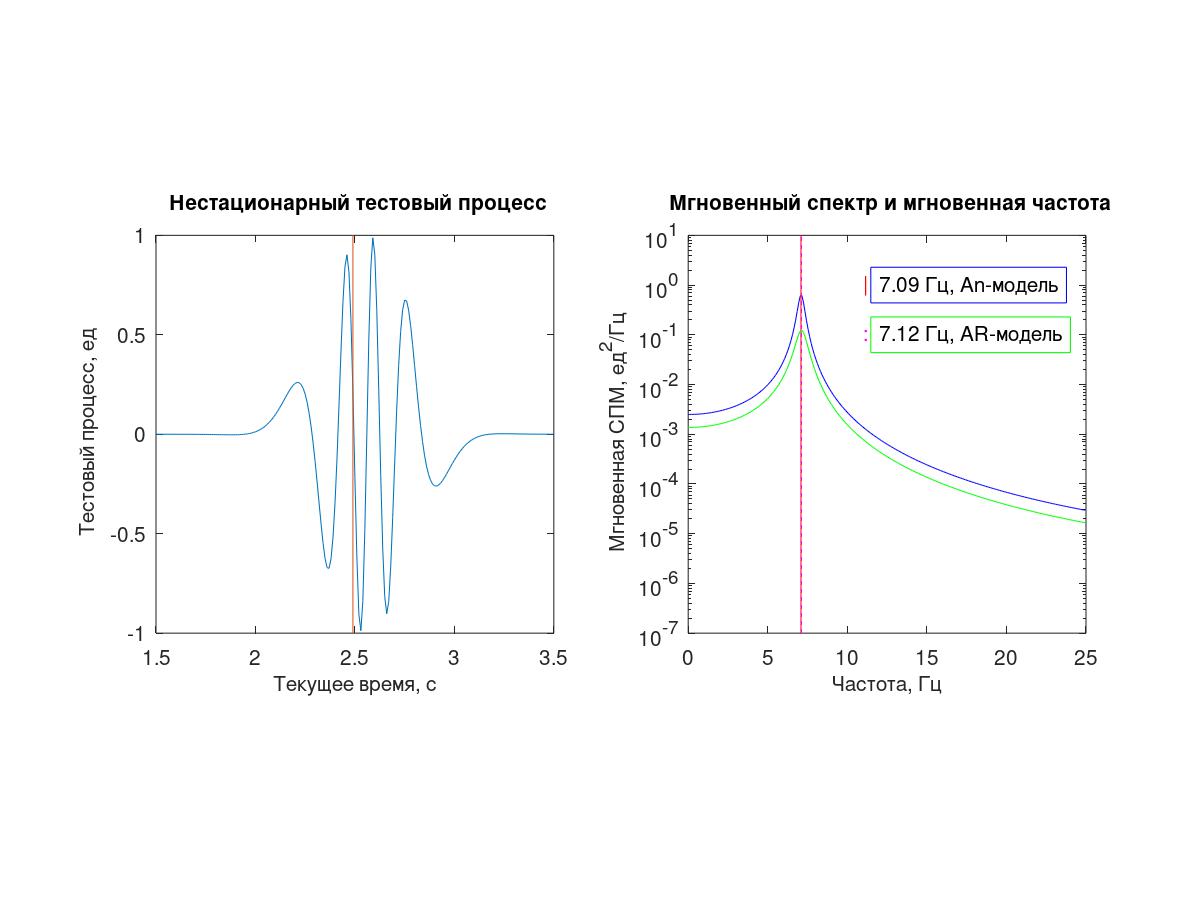
Общеизвестно, что большинство временных рядов, с которыми приходится иметь дело исследователю, являются нестационарными, и их анализ ощутимо сложнее, чем изучение стационарных процессов. Поскольку интерес к вейвлетам, похоже, пошел на убыль, полезно обсудить некоторые иные «нестационарные» инструменты, пригодные, в первую очередь, для оценки мгновенных частот, а также для оценки мгновенных спектров.
В первую очередь есть смысл вспомнить об «аналитическом сигнале». Ниже «An-моделью» именуются как раз нахождение мгновенных импеданса и мощности тестового сигнала после достройки его мнимой частью (сдвинутой по фазе на π/2).
Но не всегда есть возможность возиться с преобразованием Гилберта. Ранее уже упоминалось об авторегрессионном способе спектрального оценивания, пригодном для работы с короткими последовательностями. Под «AR-моделью» здесь будет подразумеваться исследование коротких (из 5 сэмплов) перекрывающихся фрагментов исходного сигнала с целью определения коэффициентов авторегрессии 2-го порядка, нахождение по ним «полюсов» модели и т.д.